오늘은 백준 [네트워크 연결] 문제를 풀며 최소 신장 트리의 개념에 대해 확실하게 공부를 해야겠다고 느껴 해당 포스팅을 작성해보았습니다.
1. Spanning Tree (신장 트리)
1-1) 개념
Spanning Tree?
: 그래프 내의 모든 정점을 포함하는 트리
Spanning Tree는 그래프의 최소 연결 부분 그래프 입니다.
최소 연결이란 의미는, 가장 최소한의 간선으로 모든 vertex를 연결한다는 의미입니다.
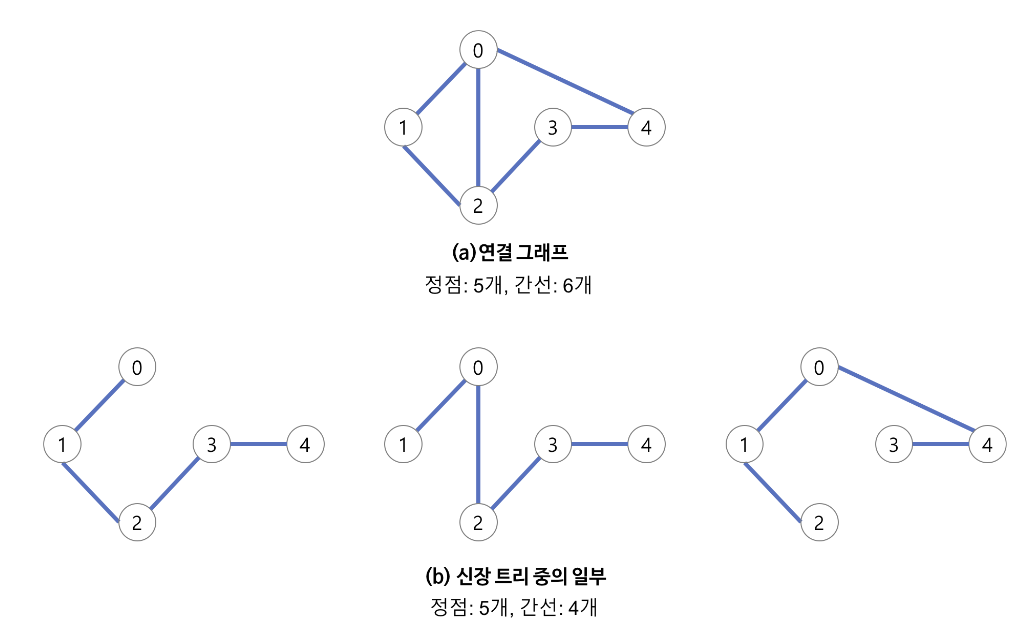
1-2) 특징
spanning tree의 특징은 다음과 같습니다.
- dfs, bfs 등을 사용하여 그래프에서 신장 트리를 찾을 수 있습니다.
- 하나의 그래프에는 많은 신장트리가 존재할 수 있습니다.
- 모든 정점이 연결 돼야 하며 사이클이 존재 X
- n개의 정점 이라면, n-1개의 간선을 가진다.
1-3) 사용 사례
가장 대표적인 문제로는 통신 네트워크 구축 문제가 있습니다.
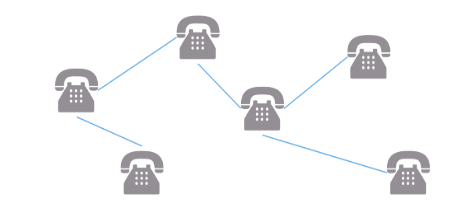
위 그림은 회사 내의 전화기를 가장 적은 간선만을 사용해 연결하고자 하는 경우입니다.
위 그림에서의 전화기 수(vertex)는 6개이고 간선 수(edge)는 5개입니다.
2. MST (최소 신장 트리)
2-1) 개념
MST (Minmum Spanning Tree) ?
: Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리
MST는 간선에 가중치를 고려하여 최소 비용의 Spanning Tree를 선택하는 것을 말합니다.
즉, 네트워크(가중치를 간선에 할당한 그래프)에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결하는 것 입니다.
2-2) 특징
- 간선의 가중치의 합이 최소 여야 한다.
- n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용해야 한다.
- 사이클이 포함되어서는 안된다.
2-3) 사용 사례
통신망, 도로망, 유통망에서 길이, 구축 비용, 전송 시간 등을 최소로 구축하려는 경우
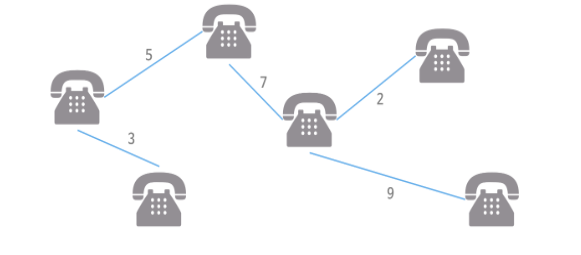
-
도로 건설
도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제 -
전기 회로
단자들을 모두 연결하면서 전선의 길이가 가장 최소가 되도록 하는 문제 -
통신
전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제 -
배관
파이프를 모두 연결하면서 파이프의 총 길이가 최소가 되도록 연결하는 문제
MST 알고리즘
1. Kruscal 알고리즘
탐욕적인 방법(greedy method) 을 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것
[과정]
- 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
- 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
- 즉, 가장 낮은 가중치를 먼저 선택한다.
- 사이클을 형성하는 간선을 제외한다.
- 해당 간선을 현재의 MST(최소 비용 신장 트리)의 집합에 추가한다.
2. Prim 알고리즘
시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장 해나가는 방법
정점 선택을 기반으로 하는 알고리즘이다.
이전 단계에서 만들어진 신장 트리를 확장하는 방법이다.
[과정]
- 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
- 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.
( -> 즉, 가장 낮은 가중치를 먼저 선택한다.) - 위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다.
3. 비교
1.시작
크루스칼 알고리즘은 최소 가중치를 갖는 Node에서 시작하지만, 프림 알고리즘은 모든 정점을 고려한다.
2. 순회
크루스칼 알고리즘은 1개의 노드에 대해서 1번만 순회하지만, 프림 알고리즘은 2번 이상 순회하게 된다.
3.시간 복잡도
프림 알고리즘은 어떤 자료구조를 이용하느냐에 따라서 차이가 나지만 크루스칼 알고리즘의 경우 변함이 없다.
4. 적합성
프림 알고리즘은 밀도가 높은 그래프에, 크루스칼 알고리즘은 밀도가 적은 그래프에서 더 빠르게 동작한다.
