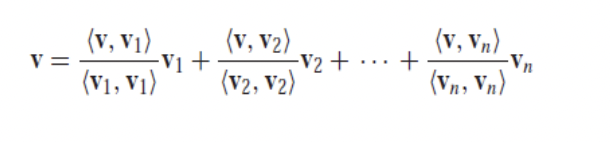내적
내적이 뭔데?
내적은 스칼라곱이라고 한다. 두 벡터의 성분을 곱한뒤 모두 더하여 얻는 값이라고 한다.
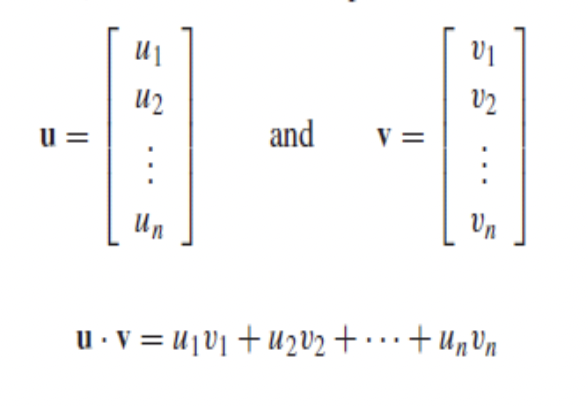
내적을 통해서 벡터의 길이도 구할 수 있다. 이 길이를 norm이라고 하기도 한다. 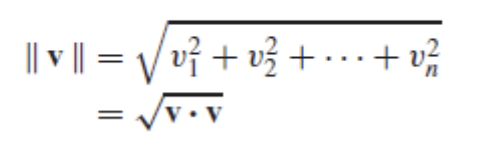
이 길이 개념은 확장시켜서 두 벡터 사이의 거리를 구할 수도 있다. 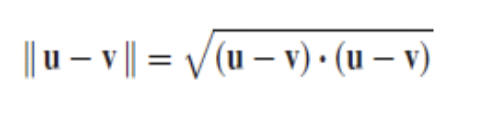
일반적으로 내적은 다음과 같은 성질을 만족한다고 한다.

코시 슈바르츠의 부등식
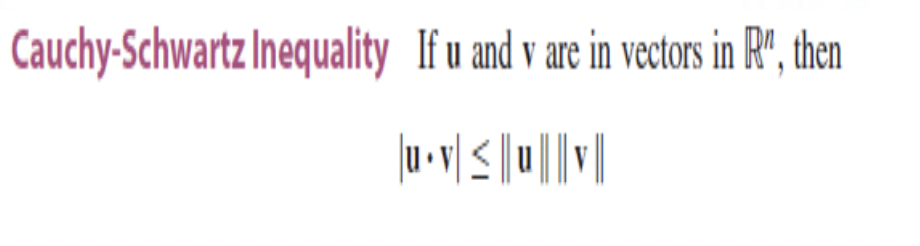
다음이 만족한다고 한다. 다음 공식의 증명 과정은 다음과 같다.
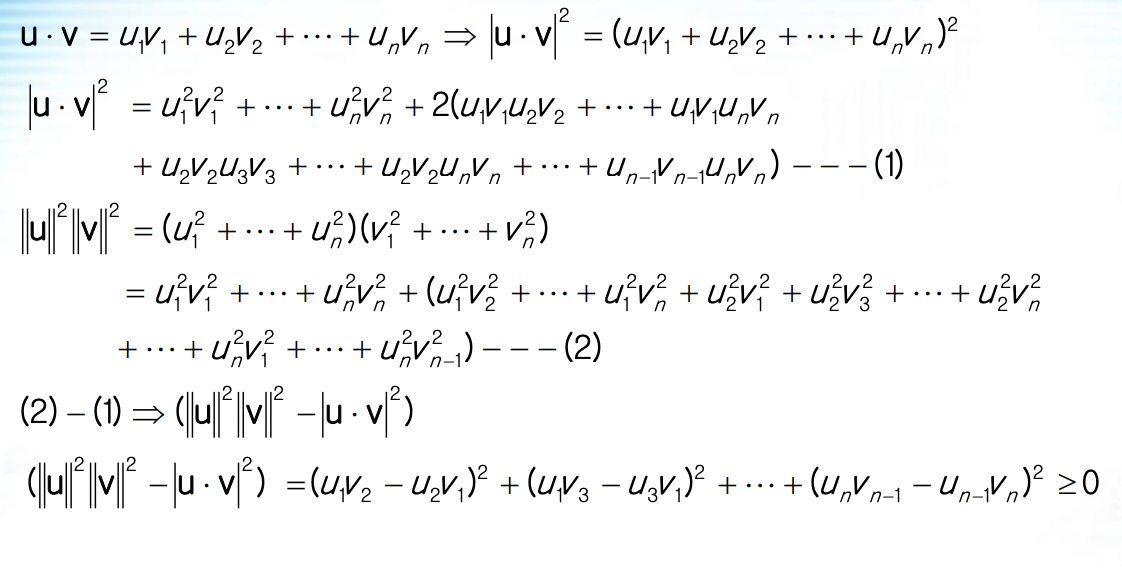
두 벡터 사이의 각도

직교 (orthogonal)
두 벡터 사이의 각도가 90도이면 직교한다고 한다.
내적 공간
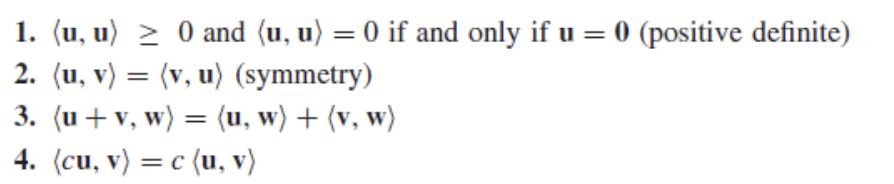
다음 4가지 공리를 만족시키는 <u, v>가 성립하는 공간을 내적공간이라고 한다.
여기서도 벡터의 norm은 다음과 같다.
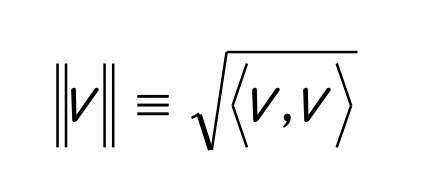
직교
공간 S에 있는 벡터들이 서로 직교이면 S는 선형적으로 독립이라고 한다. 또한 V가 n차원이면 벡터들은 V의 기저가 된다고 한다.