불균형 트리

이 전에 이진 검색 트리를 공부하면서 특이 케이스를 봤었다.
다음과 같이 트리가 굉장히 불균형 적으로 되어 있다면 이진 트리 구조를 쓰는 의미가 없다. 이진 트리의 장점은 아래로 내려가면서 내가 검색해야하는 노드의 수가 줄어 든다는 점이었다. 하지만 이런식으로 되어 있으면 거의 줄지 않는다.

때문에 이러한 문제를 해결하기 위해서 트리를 균형있게 만들어 주어야 한다. 균형 있다는 것이 무엇은가 고민해본다면 이것은 트리의 높이 혹은 깊이와 밀접한 관련이 있다. 균형 이진 트리로 되어 있다면 로그 n의 시간으로 검색 삽입 삭제를 보장할 수 있다.

AVL Tree

먼저 볼 트리를 AVL 트리이다. AVL은 그냥 사람 이름 이라고 한다. 이 트리의 특징은 모든 노드에 대해 좌서브 트리의 높이와 우서브 트리의 높이의 차가 1을 넘지 않는다는 점이다.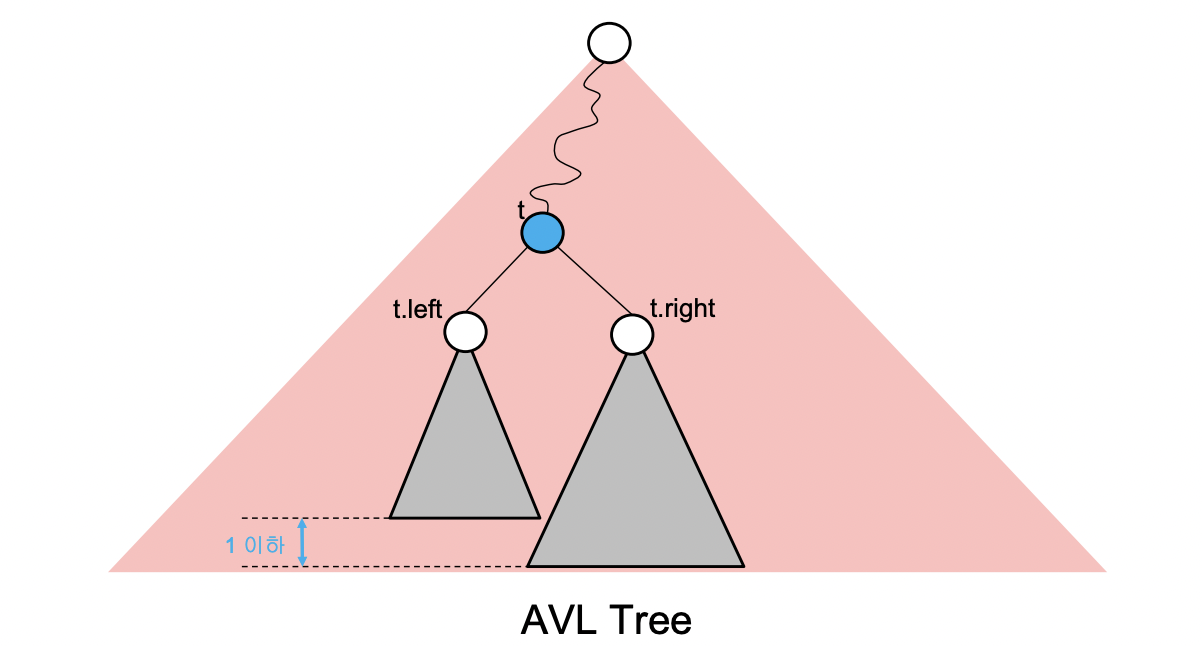

다음과 같은 식으로 트리를 만들어 주어야 한다. 변형 해준다는 표현이 더 맞을 것 같다. AVL 트리가 아닌 트리를 AVL 트리 형태로 만들어 주는게 우리가 해야할 일이다. 만들어 주는 과정은 복잡하지만 만들고 나면 짧은 시간에 연산을 진행할 수 있다는 장점이 있다.

우리는 이 과정을 수선이라고 말한다. 수선의 과정은 복잡하면서 간단하다. 일단 수선의 4가지 유형에 대해 살펴보자.

LL유형

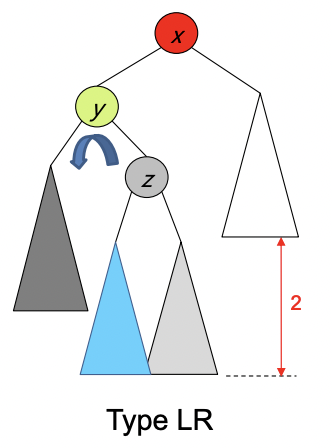
LR유형

RR 유형

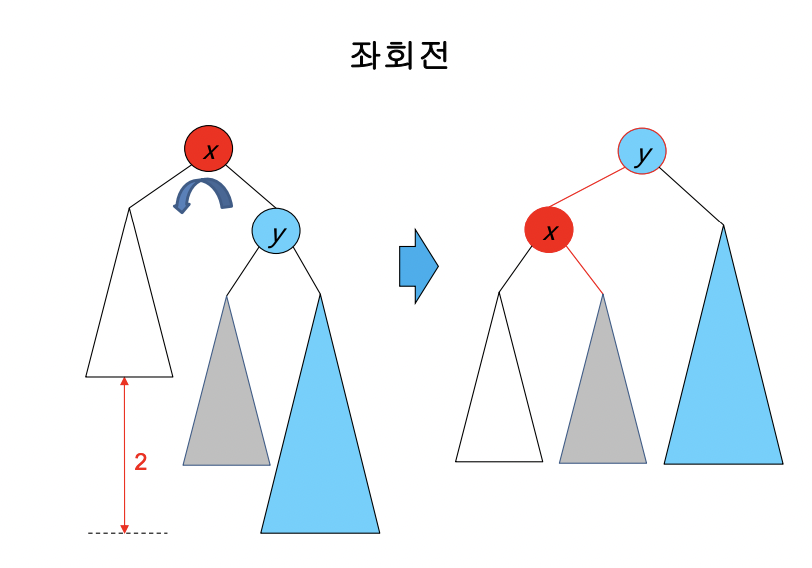
RL 유형

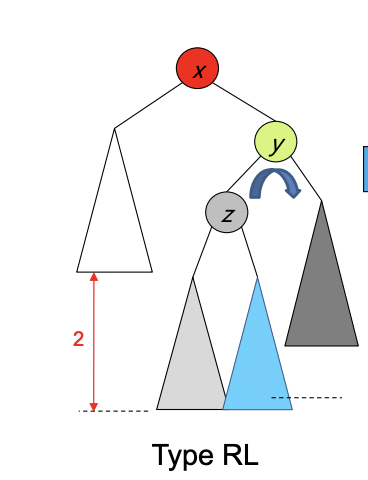
높이차 기준으로 구분하는 것 같다. 이것을 수도코드로 보면 다음과 같다.

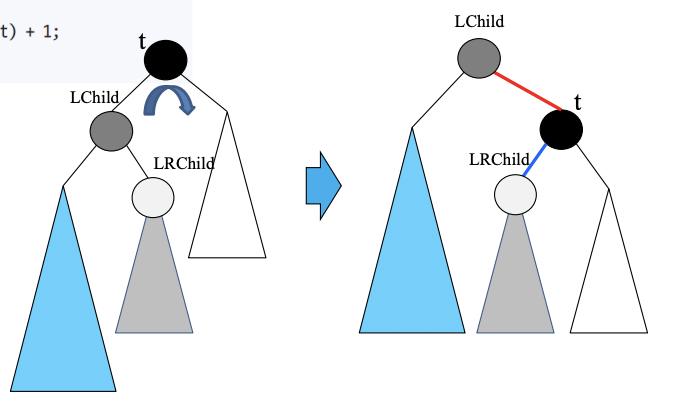
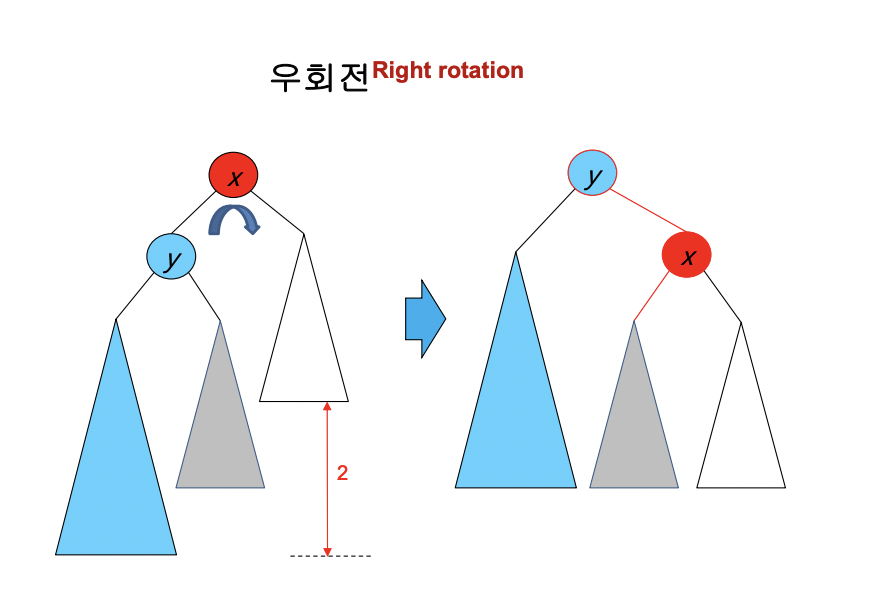
여기서 구조를 변형 해주는 것을 회전한다 라고 표현하는데 회전은 과정은 눈치 빠른 사람이면 알았을 것이다. 오른쪽 자식을 부모 위치로 올리고 오른쪽 자식의 왼쪽 서브트리를 부모의 오른쪽 서브트리로 넣어버리는 것이다. 이것이 좌회전이다. 그림으로 보면 다음과 같다.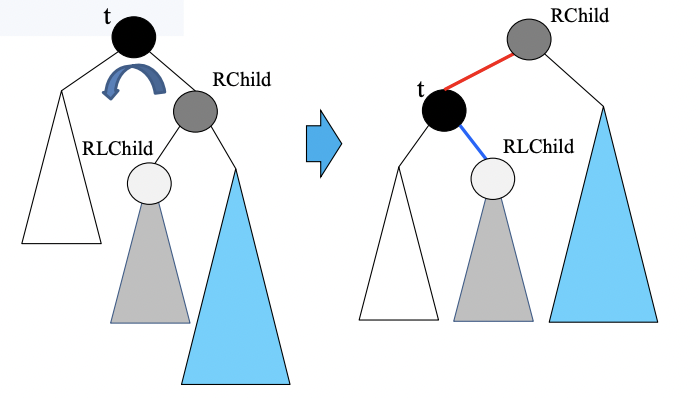

우회전은 반대의 경우로 다음과 같다.