정렬

백준 같은 사이트에서 문제를 풀 다 보면 많이 만나는 주제이다. 정렬은 다양한 방법이 있고 각각의 상황에 따라 강한 정렬도 있다. 때문에 다양한 종류의 정렬을 알고 있는 것은 꽤 중요하다고 할 수 있다. 사실 퀵 정렬을 가장 많이 사용하지만 다른 것들도 알고 있어야 한다. 또한 단순히 퀵정렬을 아는 것 뿐만 아니라 퀵정렬을 개선시킬 방법도 알고 있어야 한다.

선택 정렬 (selesction sort)

선택 정렬의 아이디어는 최대값을 가지는 원소를 찾아서 맨 뒤에 놓는 것이다.

[8, 31, 48, 73, 3, 65, 20 ,29, 11, 15]

다음과 같은 리스트가 있을 때 73이 맨 뒤로 가서 다음과 같이 된다.

[8, 31, 48, 15, 3, 65, 20, 29, 11, 73]

73과 15의 자리를 바꾸어 주는 것이다. 이를 구현한 코드는 다음과 같다.

# selectionsort / best: n ** 2 / worst: n ** 2
def selectionsort(A):
  for last in range(len(A)-1, 0, -1):
    k = A.index(max(A[:last+1]))
    A[k], A[last] = A[last], A[k]
    print(A)
array = [8, 31, 48, 73, 3, 65, 20 ,29, 11, 15]
selectionsort(array)
print(array)

선택 정렬은 어떤 리스트가 들어오던 n 번 n-1번 ''' 1번 이런 식으로 동작하기 때문에 시간 복잡도를 보면 n ** 2 이다.

거품 정렬 (bubble sort)

거품 정렬은 선택 정렬과 굉장히 유사하지만 최대 값을 찾는 방식이 조금 다르다. 거품 정렬은 뒤의 원소와 비교해서 만약 자신이 크다면 뒤의 원소와 자리를 바꾸는 방식으로 진행 된다. 선택 정렬과 동일한 리스트를 넣었을 때 거품 정렬은 다음과 같이 진행된다.

[8, 31, 48, 3, 65, 20, 29, 11, 15, 73]

단순히 맨 뒤의 원소와 자리를 바꾸는 것이 아니라 하나씩 밀리게 되는 것이다.

코드로 나타내면 다음과 같다.

# bubble sort / best: n ** 2 / worst: n ** 2
def bubblesort(A):
  for i in range(len(A), 1, -1):
    for j in range(i-1):
      if A[j] > A[j+1]:
        A[j+1], A[j] = A[j], A[j+1]
    print(A)
array = [8, 31, 48, 73, 3, 65, 20 ,29, 11, 15]
bubblesort(array)
print(array)

이 친구도 어차피 한 번씩 돌아봐야 하기 때문에 n ** 2의 시간 복잡도를 가진다.

삽입 정렬 (insertion sort)

삽입 정렬은 위의 코드들과 다르게 빠를 때도 있고 느릴 때도 있다. 이게 무슨 말이냐면 내가 넣어주는 리스트의 상태에 따라서 성능이 달라진다는 이야기이다. 만약 정렬이 되어 있는 리스트를 넣어주었을 때 위의 것들은 어차피 다 돌아봐야 하기 때문에 n ** 2이 걸리지만 삽입 정렬은 n번 걸린다. 삽입 정렬의 원리는 앞 k개의 원소를 정렬하는 방식으로 진행된다.

마찬가지로 같은 리스트([8, 31, 48, 73, 3, 65, 20 ,29, 11, 15])를 넣었을 때 삽입 정렬은

[8, 31, 48, 73, 3, 65, 20, 29, 11, 15] // k=1

[8, 31, 48, 73, 3, 65, 20, 29, 11, 15] // k=2

[8, 31, 48, 73, 3, 65, 20, 29, 11, 15] // k=3

[3, 8, 31, 48, 73, 65, 20, 29, 11, 15] // k=4

[3, 8, 31, 48, 65, 73, 20, 29, 11, 15] // k=5

다음과 같이 진행 된다.

이렇게 보면 이해가 직관적일 것이다. insert라는 개념을 직관적으로 쓰기 위해 코드를 구현할 때 파이썬의 insert를 사용해 보았다.

# lnsertion sort / best: n / worst: n ** 2
def insertionsort(A):
  for i in range(1, len(A)):
    prev = i-1
    newItem = A[i]
    
    while newItem < A[prev] and prev >= 0:
      prev -= 1
    
    A.pop(i)
    A.insert(prev+1, newItem)

    print(A)

array = [8, 31, 48, 73, 3, 65, 20 ,29, 11, 15]
insertionsort(array)
print(array)

시간 복잡도는 best: n / worst: n ** 2 이다.

병합 정렬 (merge sort)

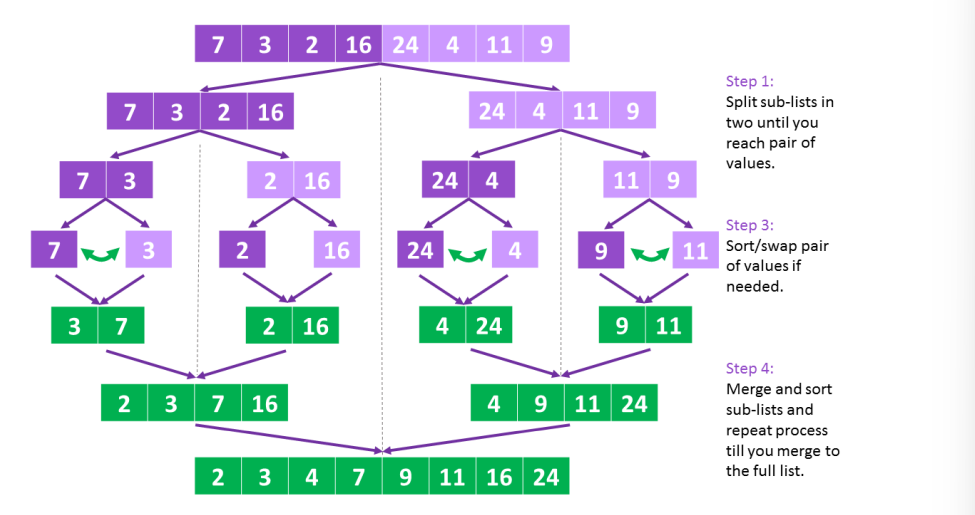
병합 정렬부터는 보통 사람의 머리에서 나오기 힘들다. 꽤나 똑똑한 사람들이 만든 정렬이다. 아이디어는 다음과 같다. 리스트를 쪼개고 쪼개서 하나로 만들고 합칠 때 정렬 해서 합치는 것이다. 무슨 말이냐고? 처음 보면 잘 이해가 안 될 수 있다.
https://www.101computing.net/merge-sort-algorithm/
다음 사이트를 보고 연습해보자.

다음 그림을 보면 조금 이해가 될 것이다. 중요한 것은 합칠 때 잘 합치는 것이다. 병합 정렬은 2개의 함수가 사용된다. 정렬을 진행해 나가는 함수와 합치는 함수이다. 또한 재귀적인 개념을 사용하기 때문에 프로그래밍을 처음 공부하는 사람들은 이해가 어려울 것이다.

우선 정렬을 진행해 나가는 함수를 살펴보자.

def mergesort(A, p, r):
  if p < r:
    q = (p+r) // 2
    mergesort(A, p, q)
    mergesort(A, q+1, r)
    merge(A, p, q, r)

다음과 같이 작성한다. p는 시작(0) 이고 r은 리스트의 끝 인덱스(len(A)-1)를 넣어주면 된다.

재귀적인 모습을 잘 살펴보자. q는 중간이다. 중간을 기준으로 mergesort를 앞에서도 진행하고 뒤에서도 진행한다.

위의 코드를 그림과 같은 리스트로 정렬하면 다음과 같이 된다.

#output
앞에 2개를 정렬한다. [7, 3] -> [3, 7] 
[3, 7, 2, 16, 24, 4, 11, 9]

2와 16을 정렬 하지만 이미 정렬됨.
[3, 7, 2, 16, 24, 4, 11, 9]

앞에 4개를 순서대로 병합.
[2, 3, 7, 16, 24, 4, 11, 9]

뒤에 4개를 같은 방식으로 정렬.
[2, 3, 7, 16, 4, 24, 11, 9]

[2, 3, 7, 16, 4, 24, 9, 11]

뒤에 4개를 순서대로 병합.
[2, 3, 7, 16, 4, 9, 11, 24]

마지막에 병합!
[2, 3, 4, 7, 9, 11, 16, 24]

논리적인 흐름을 보면 다음과 같이 된다.

이를 merge로 잘 구현하면 된다. 아이디어는 잘 쪼개진 데이터를 순서대로 잘 쌓아서 저장하기이다.

def merge(A, p, q, r):
  i = p; j = q+1; t = 0;
  tmp = [0 for i in range(len(A))]
  while i<= q and j <= r:
    if A[i] <= A[j]:
      tmp[t] = A[i]; t += 1; i += 1
    else:
      tmp[t] = A[j]; t+=1; j+=1;
  #찌꺼기 들
  while i<=q:
    tmp[t] = A[i]; t += 1; i+=1;
  while j<=r:
    tmp[t]=A[j];t+=1;j+=1;

  # 다시 저장
  i=p;t=0;
  while i<=r:
    A[i] = tmp[t]; t+=1; i+=1;
  
  print(A)

mergesort 시간 복잡도(avg): ϴ(nlogn)

merge sort는 위의 아이디어들 보다 신박하긴 하지만 나름의 단점도 존재한다.

1. A[n]과 동일한 크기의 보조 리스트 tmp[] 가 필요 => In-place sorting 이 아님
2. (-) 추가 공간 필요
3. (-) 복사 과정 발생 => A와 tmp 의 역할을 매번 바꾸면 복사 비용 개선 가능함.

퀵 정렬 (quick sort)

퀵 정렬도 보통의 사람 머리로 생각해내기 어렵다. 굉장히 재미있는 아이디어라고 생각한다. 퀵 정렬도 재귀적인 개념을 쓰기 때문에 그 흐름을 한 번에 파악하기 쉽지 않다.

def quicksort(A, p, r):
  if p<r:
    q = partition(A, p, r)
    quicksort(A, p, q-1)
    quicksort(A, q+1, r)

퀵 정렬의 아이디어는 기준으로 잡은 원소(피봇)보다 큰 값과 작은 값으로 나누는 것이다. 그림으로 보자면 다음과 같다.

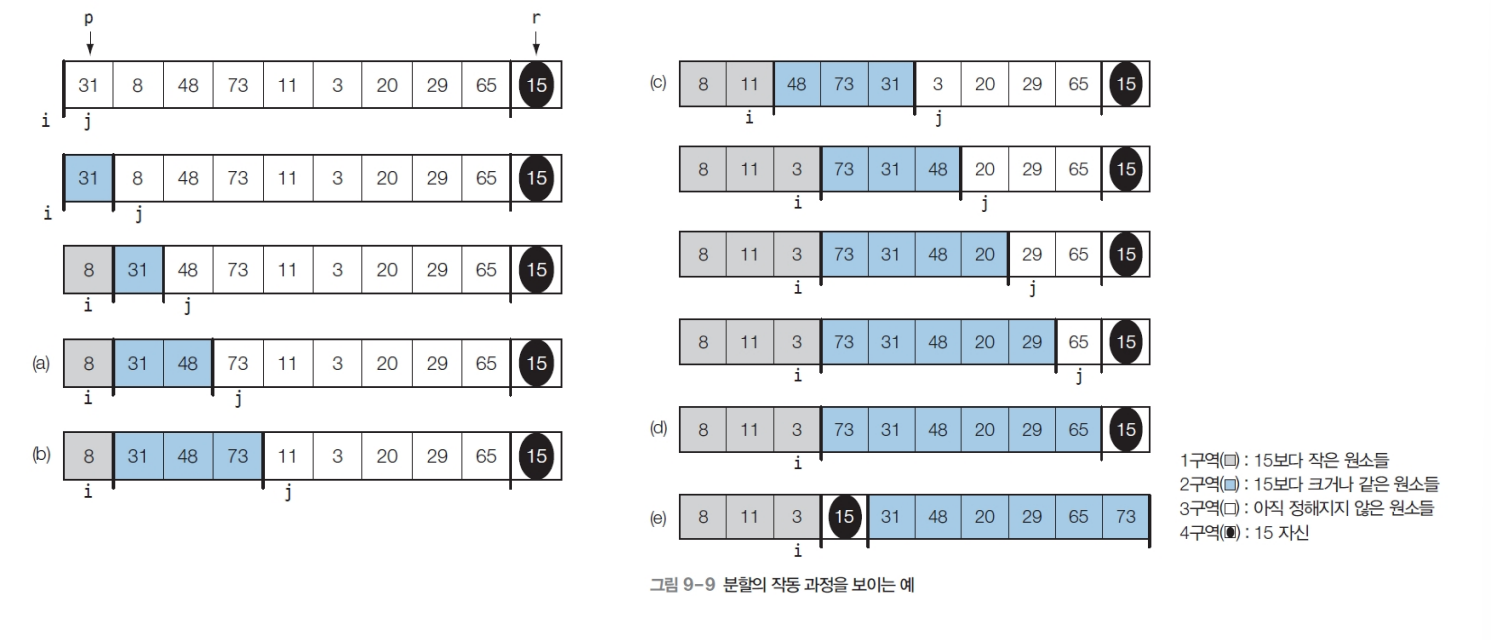
여기서 i, j, p, r의 위치를 주의 깊게 볼 필요가 있다. i는 시작할 때 -1에서 시작하는 모습을 보인다. 하지만 피봇 보다 작은 원소가 들어왔을 때 i는 +=1 을 하게 된다. 회색 영역의 끝을 i로 만든 것이다. 그리고 피봇의 위치는 i+1이 된다. 이 개념을 잘 기억해야 한다.

퀵 정렬은 병합 정렬과는 반대로 병합하는 과정이 없다. 그저 쪼갠다음에 그 쪼갠 데이터 안 에서 정렬을 진행하는 것이다.

마찬가지로 결과를 보면서 이해를 해보자.

# 결과

# 앞 부분 정렬
pivot: 15
[8, 11, 3, 15, 31, 48, 20, 29, 65, 73]
pivot: 3
[3, 11, 8, 15, 31, 48, 20, 29, 65, 73]
pivot: 8
[3, 8, 11, 15, 31, 48, 20, 29, 65, 73]

# 뒷 부분 정렬
pivot: 73
[3, 8, 11, 15, 31, 48, 20, 29, 65, 73]
pivot: 65
[3, 8, 11, 15, 31, 48, 20, 29, 65, 73]
pivot: 29
[3, 8, 11, 15, 20, 29, 31, 48, 65, 73]
pivot: 48
[3, 8, 11, 15, 20, 29, 31, 48, 65, 73]

종료 조건을 어떻게 해야할까? 내(pivot) 앞이나 뒤에 원소가 없거나 1개이면 된다. 앞에 있는 원소가 1개 이하이면 quicksort(A, p, q-1) 에서 p와 q-1의 차이는 0이하이다. 때문에 if문에서 만들어 놓은 조건에 걸리게 되면서 더 이상 진행하지 않게 된다. 뒷부분도 마찬가지 이다.

때문에 우리가 고민해야 하는 부분은 위에서 다른 퀵 정렬 개념을 코드로 옮기기만 하면 된다.

def partition(A, p, r):
  x = A[r]
  loc = p-1
  for big in range(p, r):
    if A[big] < x:
      loc += 1
      A[loc], A[big] = A[big], A[loc]
  A[loc+1], A[r] = A[r], A[loc+1]
  
  print("pivot:", A[loc+1])
  print(A)

  return loc + 1

quicksort / Average/Best case: Θ (nlogn) / Worst case: Θ (n**2)

퀵 정렬의 성능이 좋지 않은 경우 / 분할이 균등하게 (예: n/2) 되지 않는 경우
/ 모두 (역)정렬 되어 있는 경우 Worst case
/ 모든 원소가 동일한 경우 Worst case

성능 저하를 방지하는 방법

피벗 원소를 양끝 값보다는 임의의 값으로 선택 (randomization)
피벗 원소와 동일 원소가 나왔을 때 양쪽으로 적절히 보내기