문제 풀이에 들어가기에 앞서서 DP에 대해서 먼저 찾아봤다.

[동적 계획법 - Dynamic Programing] DP란?

• 하나의 큰 문제를 작은 문제로 나누어 해결하는 기법을 의미.
• 기존의 재귀적인 문제 풀이 방법으론 이전의 값(같은 값)을 여러 번 구하는 문제점이 있음

→ N이 커질 수록 기하급수적으로 비효율적인 프로그램이 됨.

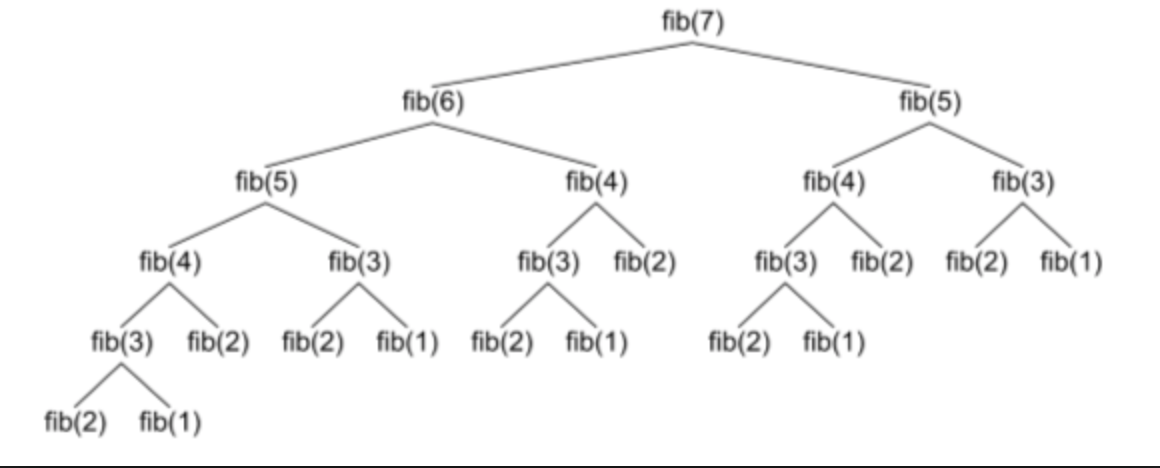
• 그래서 이미 한 번 구한 값은 배열 등에 저장해두고 다시 필요하면 재귀를 돌릴 필요 없이 저장된 값을 불러오면 문제를 해결할 수 있다.
• 재귀 함수만을 사용하면 점화식으로 문제를 푸는 것이지만, 메모이제이션까지 이용하여 DP, 문제를 작은 문제로 분해 후 해결하는 것이다.
• DP를 적용하는 단계에서 구현을 할 때, 보통 두 가지 방법이 있다. 각각 Top-Down방식과 Botton-Up방식이다.

→ Botton-Up방식은 말 그대로 초기조건을 기반으로 차곡차곡 데이터를 쌓아가 큰 문제의 결과를 도출하는 과정이다. 보통 반복문을 사용한다. 예를 들어 메모이제이션을 위한 배열 dp[]가 있었다면, dp[0] 부터 차례로 값을 채운다. Bottom-Up에 한하여 이러한 값 채우기를 본 떠 메모이제이션을  Tabulation이라 부르기도 한다.

→ Top-Down방식은 주로 재귀함수를 사용하며 dp[n]값을 찾기 위한 재귀 함수의 호출이 dp[0](또는 초기 조건까지) 내려간 다음 결과들이 재귀 함수에 맞물리며 재활용되는 방식이다.

💡

메모이제이션(memoization)이란 입력값에 대한 결괏값을 저장해둠으로써 같은 입력값에 따른 함수의 실행이 중복해서 일어나지 않도록 해주는 기법이다. DP로 문제를 풀 때 자주 등장하며, 함수의 중복 호출을 방지해 효율을 높여준다. 

추가적으로 분할정복도 DP와 함께 자주 언급된다고 한다. 두 기법은 모두 문제를 소문제로 나누어 해결한다는 공통점이 있지만, 분할정복은 하위 문제에서 중복이 일어나지 않는 방면, DP는 하위 문제에서 중복이 일어난다는 차이점이 있다.

---

DP 성립 조건 체크리스트

• 최적 부분 구조: 전체 최적해가 하위 문제들의 최적해 조합으로 표현된다.
• 중복 하위 문제: 동일하거나 동형인 하위 문제가 반복해서 등장한다.
• DFS , BFS 문제: DFS , BFS 로 풀 수 있지만 경우의 수가 너무 많은 문제.
• 최악의 경우의 수를 계산하는 가장 쉬운 방법은 직접 계산해보는 것.
• 특정 패턴을 찾을 때 까지 직접 계산해보는 것도 하나의 방법이다.
• 중복 연산이 많은 문제: 각 위치까지 올 수 있는 최적의 값만 남겨두고 나머지 값들은 다 버린 후, 남겨진 값들 중 가장 좋은 조합을 추리는 식으로 풀이.

---

구현 방식 두 가지

용어 정리: Top-Down = 하향식(메모이제이션), Bottom-Up = 상향식(타뷸레이션)

구분	Top-Down (하향식, Memoization)	Bottom-Up (상향식, Tabulation)
아이디어	큰 문제에서 시작해 필요한 하위 문제만 재귀로 계산·캐싱	기저 상태부터 테이블을 순서대로 채워 올라간다
구현	재귀 + 캐시(배열/맵)	반복문 + DP 테이블
장점	필요한 상태만 계산해 스파스한 경우 유리, 직관적	호출 스택 없음, 상수 오버헤드 작음
단점	깊은 재귀는 스택 오버플로우 위험, 재귀 오버헤드	모든 상태를 채울 때 불필요 계산 가능, 전개 순서 설계 필요
메모리	캐시 + 호출 스택	테이블, 롤링 배열로 축소 가능

---

피보나치로 보는 DP 필요성

• 순수 재귀: f(n)=f(n-1)+f(n-2) 호출이 중복되어 시간 복잡도 O(2^n)까지 커진다.
• DP 적용: 한 번 계산한 값을 저장하고 재사용하면 O(n)으로 줄일 수 있다.

---

복잡도 비교

• 피보나치수열은 대표적인 동적 프로그래밍의 사례.
• 피보나치수열을 보면 DP와 비슷하는데 피보나치수열과 DP의 차이점은 재사용.

public class Fibonacci {
	public static void main(String[] args) {
		int input = 6;

        System.out.println(fibo(input));
     }

     public static int fibo(int n) {
if (n <= 1) return n;
else return fibo(n-2) + fibo(n-1);
     }
}

// 결과 : 8

숫자가 작을 때는 차이는 없지만 숫자가 커지면 속도가 심각하게 저하된다. 만약 위 코드에서 input이 40이어도 시간이 걸리는 게 눈에 보이고 만약 100이라면 정말 오래 걸릴 것이다.

• 순수 재귀: 시간 O(2^n)
• Top-Down / Bottom-Up: 시간 O(n)
• 공간
  • Top-Down: O(n) 캐시 + 최악 O(n) 재귀 스택
  • Bottom-Up: O(n) 테이블 → 롤링 기법으로 O(1)까지 축소 가능

---

메모이제이션 핵심

• 중복 계산 제거: 이미 구한 값을 캐시에 저장해 재사용한다.
• 캐싱 자료구조 선택: 인덱스가 명확하면 배열, 상태가 복합이면 해시맵.
• 효과: 지수 시간을 선형·다항 시간으로 대폭 감소시킨다.

---

언제 무엇을 쓰나

• Top-Down 권장
  • 필요한 상태만 일부 계산하면 되는 희소 상태 공간
  • 전이 로직이 복잡하고 재귀로 쓰면 의미가 잘 드러날 때
• Bottom-Up 권장
  • 전개 순서가 명확하고 모든 상태를 채우는 게 자연스러울 때
  • 재귀 깊이가 커서 스택 위험을 피해야 할 때

---

적용 시 체크 포인트

• 기저 사례(Base Case) 를 정확히 둔다.
• 전이식(Recurrence) 이 최적 부분 구조를 보장하는지 확인한다.
• 상태 정의/차원 을 최소화해 불필요한 차원을 줄인다.
• 메모리 최적화 가 필요하면 롤링 배열 등으로 압축한다.
• DP 부적합 사례
  • 하위 최적해의 조합이 전체 최적해를 보장하지 않는 경우
  • 하위 문제가 매번 달라 중복이 거의 없는 경우

---

예시 코드

Top-Down (하향식, 메모이제이션)

import java.util.*;

class FibTopDown {
    static long[] dp;

    static long fib(int n) {
        if (n <= 1) return n;
        if (dp[n] != -1) return dp[n];
        dp[n] = fib(n - 1) + fib(n - 2);
        return dp[n];
    }

    public static void main(String[] args) {
        int n = 50;
        dp = new long[n + 1];
        Arrays.fill(dp, -1);
        System.out.println(fib(n));
    }
}

Bottom-Up (상향식, 타뷸레이션, 롤링 배열)

class FibBottomUp {
    static long fib(int n) {
        if (n <= 1) return n;
        long prev2 = 0, prev1 = 1; // f(0), f(1)
        for (int i = 2; i <= n; i++) {
            long cur = prev1 + prev2;
            prev2 = prev1;
            prev1 = cur;
        }
        return prev1;
    }

    public static void main(String[] args) {
        int n = 50;
        System.out.println(fib(n));
    }
}

---

요약

• DP 적용 조건은 최적 부분 구조 + 중복 하위 문제 이다.
• 구현은 Top-Down(메모이제이션) 과 Bottom-Up(타뷸레이션) 으로 나뉜다.
• 피보나치처럼 저장·재사용만으로 O(2^n) → O(n) 으로 개선된다.

출처:
https://dense.tistory.com/entry/dp
https://pixx.tistory.com/163

참고:

https://www.youtube.com/watch?v=0bqfTzpWySY&t=160s

---

문제 풀이

문제 선정

• 모든 문제를 다시 다 풀어보기엔 시간이 비효율적인 것 같아서 내가 나름대로 내 기준을 정하여 문제를 선정해봤다…..

1. 골드 문제는 모두 선정하였다. 일단 기본적으로 골드 문제라는 건 문제 난이도가 좀 있다는 것이고 , 난이도가 있는 만큼 자세히 짚어보고 넘어가는 것이 좋다고 생각했다.
2. 내가 틀렸던 문제들을 선정하였다. 이유는 약간 이기적이긴 하다 … 내가 틀렸던 문제를 다시 한 번 풀어보기 위해서 선정했다.
3. 창의적인 방법으로 문제를 풀어야하는 문제들을 선정해봤다.

---

1) 1463번 : 1로 만들기 (실버 3)

• 문제 :

정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지 이다.

1. X가 3으로 나누어 떨어지면, 3으로 나눈다.
2. X가 2로 나누어 떨어지면, 2로 나눈다.
3. 1을 뺀다.

정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.

---

문제 풀이

1) 처음에 주목한 점

목표 값이 1이고, 그 목표값을 구하기 위한 조건들을 봤다.

사용할 수 있는 연산이 ÷2, ÷3 , -1 이기 때문에 연산들을 이용하여 조건문을 완성해주면 원하는 코드를 얻을 수 있다고 생각했다.

i % 2 == 0, i % 3 == 0 같은 if문으로 가능한 연산만 후보로 삼아야 한다고 판단했다.

그리고 연산을 사용하는 횟수의 최솟값을 출력하라는 것이다.

이 부분이 헷갈렸던 부분인데 예제를 보면 10을 큰 수부터 나눠보기 시작하면 10 -> 5 -> 4 -> 2 -> 1 이렇게 4번의 연산이 필요하다. 하지만 정답은 10 -> 9 -> 3 -> 1 로 3이 정답이다.

또한 내가 재출한 코드에서는 구현하진 않았는데 , 내가 참고한 자료에선 2와 3의 배수, 즉 6으로 나눠지는 경우의 수도 있다. 내가 이 부분은 따로 구현하지 않았는데 통과된 이유는 ÷6은 결국 두 번의 허용 연산으로 이루어 지기 때문에 DP 점화식이 이미 그 경우를 자연스럽게 포함하고 있다고 한다.

그럼 코드로 짠다면 다음과 같은 경우의 수로 나눌 수 있겠다.

---

1. 입출력 초기화

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] dp = new int[n + 1];

dp[1] = 0;

• 나는 사실 탑다운, 바텀업이라는 개념 자체를 모르고 출발해서 잘은 몰랐지만 , 내가 풀이한 방식은 바텀업 방식이라고 한다. 무의식적으로 나는 바텀업을 선호하고 있었나보다.
• 바텀업 방식을 사용하게 된다면 필요한 값이 항상 준비돼 있게되어서 계산이 편해진다.
• 먼저 전에 계산한 값을 저장해두기 위해 dp 배열을 선언해주고 있고, 인덱스 1..n을 쓰므로 크기를 n+1로 할당해주었다.
• 1은 이미 1이므로 연산 0번이라 초기값을 → dp[1] = 0 이렇게 초기화해두었다.

2. 점화식과 반복

for (int i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + 1;                 // 기본 후보: 1을 빼는 연산
    if (i % 2 == 0) dp[i] = Math.min(dp[i], dp[i / 2] + 1);  // 2로 나눠떨어지면 후보 갱신
    if (i % 3 == 0) dp[i] = Math.min(dp[i], dp[i / 3] + 1);  // 3으로 나눠떨어지면 후보 갱신
}

• dp[i]는 “마지막 연산이 무엇이었는지”에 따라 다음 후보 중 최솟값을 결정한다.
  • i → i-1을 마지막에 했다면 dp[i-1] + 1
  • i가 2의 배수라면 i → i/2 가능 → dp[i/2] + 1
  • i가 3의 배수라면 i → i/3 가능 → dp[i/3] + 1
• 먼저 dp[i-1] + 1로 초기 세팅한 뒤, 조건이 맞을 때만 min으로 갱신해주었다.
• 이런식으로 dp[2] 부터 dp[n] 까지의 계산 결과를 저장해둔다.
• 예를 들어 dp[9]를 계산할 땐 (dp[8], dp[3]) 결과에서 dp[9]는 dp[8] 기준으로 -1 연산을 한 번 추가해준 거기 때문에 (dp[8] + 1) 해서 4가 나오지만 , dp[3] 기준에선 ÷3 연산을 한 번 추가해준 것이기 때문에 (dp[3] + 1 ) = 3 이 되어 Math.min 함수가 두 수중에 더 낮은 숫자를 골라주어 dp[9] = 3 이 되는 원리이다.

전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] dp = new int[n + 1];
    
    dp[1] = 0;

    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + 1;
        if (i % 2 == 0) dp[i] = Math.min(dp[i], dp[i / 2] + 1);
        if (i % 3 == 0) dp[i] = Math.min(dp[i], dp[i / 3] + 1);
    }

    System.out.println(dp[n]);
    br.close();
  }
  
}

참고 : https://st-lab.tistory.com/133

---

2) 11726번: 2×n 타일링 (실버 3)

• 문제 요약: 2×n 직사각형을 1×2(세로), 2×1(가로) 타일로 빈틈없이 채우는 방법의 수를 구해라. 정답은 10007로 나눈 나머지를 출력한다.
  

---

문제 풀이

1) 처음에 주목한 점

• 최종 목표는 “방법의 수”이다! 이때 나는 타일 배치에 주목을 해봤다. 타일의 마지막 형태를 보면 선택지가 2개로 나온다.
  • 마지막 한 열(세로 1칸 폭)을 세로 타일(1×2) 하나로 채우거나,
  • 마지막 두 열(가로 2칸 폭)을 가로 타일(2×1) 두 개로 채운다.
• 이 관찰에서 자연스럽게 작은 문제로 쪼개지는 구조가 나온다.

2) 점화식 도출

• dp[i] = 2×i 보드를 채우는 방법의 수
• 마지막 배치에 따라:
  • 마지막에 세로를 세우면 남은 모양은 2×(i−1) → dp[i−1]
  • 마지막에 가로 두 개를 깔면 남은 모양은 2×(i−2) → dp[i−2]
• 따라서,

  dp[i] = dp[i−1] + dp[i−2]

• dp[1] = 1 ← 세로 1×2 ( 한 가지 !! )
• dp[2] = 2 ← 세로 1×2 두 장, 혹은 가로 2×1 두 장 ( 두 가지 !! )

---

1. 입출력/초기화

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] dp = new int[n + 1];

dp[1] = 1;
if (n >= 2) dp[2] = 2;

• dp[i]는 “2×i를 채우는 방법 수” 이다.
• 먼저 dp[1]=1, dp[2]=2를 기저로 두었다.
• n=1인 입력도 있으므로 dp[2] 대입은 조건부(n≥2)로 처리해주었다.

2. 점화식과 반복

for (int i = 3; i <= n; i++) {
    dp[i] = (dp[i - 1] + dp[i - 2]) % 10007;
}

• 마지막 배치 기준의 두 경우(i−1, i−2)를 더해주었다 !!
• 그리고 문제에서 10007 모듈러 계산을 하라고 해서 코드를 넣었는데 아마 너무 수가 커지는 걸 방지해주는 것 같다.

전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int[] dp = new int[n + 1];

        dp[1] = 1;
        if (n >= 2) dp[2] = 2;

        for (int i = 3; i <= n; i++){
            dp[i] = (dp[i - 1] + dp[i - 2]) % 10007;
        }

        System.out.println(dp[n]);
        br.close();
    }
}

참고: https://www.youtube.com/watch?v=HmvD3X5pme8&t=437s

---

3) 11727번: 2×n 타일링 2 (실버 3)

• 문제 요약: 11726과 거의 같은데, 타일 종류에 2×2가 추가된다. 정답은 10007로 나눈 나머지.
  

문제 풀이

1) 처음에 주목한 점

• 11726에서 나는 “마지막 배치”를 기준으로 dp[i] = dp[i-1] + dp[i-2]를 만들었었다.
• 11727에서는 마지막 두 열을 덮는 방법이 1가지가 아니라 2가지가 된다:
  • (A) 가로 타일(2×1) 두 개를 위아래로 쌓기
  • (B) 2×2 타일 한 장
• 그래서 i-2 부분이 두 배가 된다. 즉,

  dp[i] = dp[i-1] + 2*dp[i-2]

2) 점화식 도출

• dp[i] = 2×i 보드를 채우는 방법의 수
• 마지막 배치에 따라:
  • 세로(1×2) 한 장으로 마지막 한 열을 채우면 → 남은 건 2×(i−1) → dp[i−1]
  • 마지막 두 열을 채우는 방법이 2가지:
    • (A) 가로(2×1) 두 장 → dp[i−2]
    • (B) 2×2 한 장 → dp[i−2]
  • 합치면 dp[i−2] + dp[i−2] = 2*dp[i−2]
• 따라서 dp[i] = dp[i−1] + 2*dp[i−2]
• 기저값
  • dp[1] = 1
  • dp[2] = 3 (세로×2, 가로×2, 2×2 한 장 → 총 3가지)

---

1. 입출력/초기화

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[] dp = new int[n + 1];

dp[1] = 1;
if (n >= 2) dp[2] = 3;

• 11726과 동일한 흐름이지만 dp[2] 값이 2 x 2 때문에 3으로 바뀐다

2. 점화식과 반복

for (int i = 3; i <= n; i++){
    dp[i] = (dp[i - 1] + dp[i - 2] + dp[i - 2]) % 10007; // = dp[i-1] + 2*dp[i-2]
}

• dp[i - 2] 에서 마지막 두 열을 덮는 방법이 (가로×2, 2×2)로 두 가지이기 때문에 2번 더해준다 !

전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
public static void main(String[] args) throws IOException {
	BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
	int n = Integer.parseInt(br.readLine());
	int[] dp = new int[n + 1];
	    dp[1] = 1;
	    if(n >= 2) dp[2] = 3;

	    for(int i = 3; i <= n; i++){
	        dp[i] = (dp[i - 1] + dp[i - 2] + dp[i - 2]) % 10007;
	    }

	    System.out.println(dp[n]);

	    br.close();
	 }
}

---

4) 9461번: 파도반 수열 (실버 3)

• 문제 요약: 여러 개의 테스트 케이스에 대해 P(n)을 구해 출력한다. (입력: T개, 각 n은 1 ≤ n ≤ 100)
  

---

문제 풀이

1) 접근 방법

• 나는 먼저 dp[1]부터 dp[5]까지의 배열을 먼저 대입해봤다. 그리고 난 다음에 이 배열안에 숨겨진 수열을 찾으려고 했다.

2) 점화식(핵심 규칙)

• 파도반 수열의 앞 값들을 보면: 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, ... 처럼 되어있따 ! 이 배열을 보면 한가지 규칙이 있다는 걸 눈치챌 수 있다. n이 6 이상일 때 부터 n-2 번째와 n-3 번째의 수를 합 한 것이 자신의 숫자가 되는 걸 알아차릴 수 있었고 , 그걸 식으로 나타내면

  P(n) = P(n-2) + P(n-3)    (n ≥ 6)

• 기저값:

  P(1)=P(2)=P(3)=1
  P(4)=P(5)=2

• 수가 커질 수 있어서 long 사용해줘야했다 !! 나는 int 형 사용했다가 출력 형태 오류로 틀렸다.

3) 구현 포인트

• dp[1..100]을 한 번 채워두고, 각 n에 대해 dp[n] 출력

---

전체 코드 (내 코드)

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int T = Integer.parseInt(br.readLine());
        long[] dp = new long[101];

        dp[1] = dp[2] = dp[3] = 1;
        dp[4] = dp[5] = 2;

        for (int i = 6; i <= 100; i++) {
            dp[i] = dp[i - 2] + dp[i - 3];
        }

        for (int t = 0; t < T; t++) {
            int n = Integer.parseInt(br.readLine());
            System.out.println(dp[n]);
        }
    }
} 

참고: https://st-lab.tistory.com/127

---

5) 2011 : 암호코드 (골드5)

• 문제 요약: 1→A, 2→B, …, 26→Z로 매핑할 때, 주어진 숫자 문자열을 해석할 수 있는 경우의 수를 구한다. 해석이 불가능하면 0을 출력하고, 결과는 1,000,000으로 나눈 나머지를 출력한다.
  

---

문제 풀이

1) 처음에 주목한 점

• 한 자리(1~9)는 그 자리만 해석할 수 있고, 두 자리(10~26)는 앞자리와 묶어서 해석할 수 있다.
• 그래서 어떤 위치 i를 해석할 때 두 가지 선택이 생긴다:
  • 현재 자리만 해석(한 자리) → … + dp[i-1]
  • 앞자리와 함께 해석(두 자리) → … + dp[i-2]
• 단, ‘0’은 단독으로 해석할 수 없고, 10/20만 유효하다.

2) 점화식 도출

• dp[i] = 앞에서부터 i자리까지 해석하는 경우의 수 (편하게 쓰려고 빈 문자열도 한 경우로 보고 dp[0] = 1로 둔다.)
  
• 한 자리 유효(현재 문자 1~9)면: dp[i] += dp[i-1]
• 두 자리 유효(앞 두 문자 10~26)면: dp[i] += dp[i-2]
• 각 단계에서 dp[i] %= 1_000_000

---

1. 입출력/초기화

BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String s = br.readLine();
int n = s.length();

int[] dp = new int[n + 1];
dp[0] = 1;

if (s.charAt(0) == '0') {
	System.out.println(0);
	return;
} else {
		dp[1] = 1;
}

• dp[0]=1: 빈 문자열은 1가지로 취급(점화식 편의를 위한 표준 트릭).
• 첫 글자가 ‘0’이면 시작부터 해석 불가 → 바로 0 출력.
• 그렇지 않으면 첫 글자는 1~9이므로 dp[1]=1.

2. 점화식과 반복

for (int i = 2; i <= n; i++) {
    int one = s.charAt(i - 1) - '0';         // 한 자리
    int two = Integer.parseInt(s.substring(i - 2, i)); // 두 자리

    if (one >= 1 && one <= 9) {
        dp[i] = (dp[i] + dp[i - 1]) % 1000000; // 현재 자리만 해석
    }
    if (two >= 10 && two <= 26) {
        dp[i] = (dp[i] + dp[i - 2]) % 1000000; // 앞자리와 묶어 해석
    }
}
System.out.println(dp[n]);

• one이 1~9면 한 자리 해석 가능 → dp[i-1] 더함.
• two가 10~26이면 두 자리 해석 가능 → dp[i-2] 더함.
• ‘0’은 단독 불가이므로 one==0이면 첫 조건이 자동으로 스킵된다. 대신 two==10 또는 two==20일 때만 두 자리로 처리되어 살아남는다.
  

전체 코드

import java.io.*;

public class Main {

~~~~    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String s = br.readLine();
        int n = s.length();

        int[] dp = new int[n + 1];
        dp[0] = 1;

        if (s.charAt(0) == '0') {
            System.out.println(0);
            return;
        } else {
            dp[1] = 1;
        }

        for (int i = 2; i <= n; i++) {
            int one = s.charAt(i - 1) - '0';
            int two = Integer.parseInt(s.substring(i - 2, i));

            if (one >= 1 && one <= 9) {
                dp[i] = (dp[i] + dp[i - 1]) % 1000000;
            }
            if (two >= 10 && two <= 26) {
                dp[i] = (dp[i] + dp[i - 2]) % 1000000;
            }
        }

        System.out.println(dp[n]);
    }
}

참고: https://tussle.tistory.com/1137

---

6) 2133번: 타일 채우기 (3×n) (골드4)

• 문제 요약: 3×n 보드를 2×1, 1×2 타일로 채우는 방법의 수를 구한다. n이 홀수면 애초에 채울 수 없으므로 0.
  

---

문제 풀이

1) 처음에 주목한 점

• 3×n을 채우려면 가로 폭이 짝수여야 한다. (홀수면 어떤 식으로도 채울 수 없음)
• 기본 블록(3×2)을 붙이는 경우 외에, 특수 무늬들이 더해져서 단순한 피보나치형이 아니라 누적 합이 들어가는 점화식이 된다.

2) 점화식 도출

• dp[i] = 3×i 보드를 채우는 방법의 수 로 가정했다.
• n이 홀수면 애초에 못 채운다 → 0.
• 작은 케이스를 기준으로 규칙을 만든다:
  • dp[0] = 1 : 아무것도 안 놓는 1가지
  • dp[2] = 3 : 3×2를 채우는 3가지 기본 패턴
• 점화식 (i는 짝수, i ≥ 4)
  • 기본 3가지 패턴로 시작: 3 * dp[i-2]
  • 그 외 특수 무늬들이 i-4, i-6, … 에서 새로 조합되어 각각 2가지씩 추가됨 → 2 * (dp[i-4] + dp[i-6] + ... + dp[0])
    
• 합치면:

  dp[i] = 3*dp[i-2] + 2*(dp[i-4] + dp[i-6] + ... + dp[0])   (i는 짝수, i≥4)

3) 예시! ( Velog 참고 )

• N=2 → 3가지 → DP[2]=3
• N=4 → 3*DP[2]=9에 특수 무늬 2개 추가 → DP[4]=11
• N=6 → 3*DP[4] + 2*DP[2] + 2*DP[0] = 3*11 + 2*3 + 2*1 = 41

---

1. 입출력/초기화

int n = Integer.parseInt(br.readLine());
int[] dp = new int[n + 1];

if (n % 2 == 1) {
    System.out.println(0); // 홀수는 불가능
    return;
}

dp[0] = 1;
dp[2] = 3;

• 홀수 예외를 초반에 조건식으로 정리하여 필터링 해주었다.
• dp[0]=1은 뒤에 나올 짝수들을 매핑하기 위해서 처음에 초기화 해주었다!

2. 점화식과 반복

for (int i = 4; i <= n; i += 2) {
    dp[i] = dp[i - 2] * 3;           // 기본 3가지 패턴
    for (int j = i - 4; j >= 0; j -= 2) {
        dp[i] += dp[j] * 2;          // 누적 특수 무늬(각 2가지)
    }
}
System.out.println(dp[n]);

• 바깥 루프는 우리가 짝수 파트만 다루면 되기 때문에 짝수 폭만 진행하게 만들었다.
• 안쪽 루프가 dp[i-4], dp[i-6], …, dp[0]를 모두 더해 특수 무늬를 반영한다.

---

전체 코드

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int[] dp = new int[n + 1];

        if (n % 2 == 1) {
            System.out.println(0); // 홀수 n은 채울 수 없음
            return;
        }

       // 타일이 없을 경우의 수는 아무것도 채우지 않는 경우이다
        dp[0] = 1;

        // 3x1 타일을 채울 수 있는 경우의 수는 0개이다.
        dp[1] = 0;

        // 3x2 타일을 채울 수 있는 경우의 수는 3개이다.
        dp[2] = 3;

				// N은 홀수가 될 수 없고 짝수만 될 수 있기 때문에 2씩 증가를 한다.
        for (int i = 4; i <= n; i += 2) {
            dp[i] = dp[i - 2] * dp[2] + 2;
            for (int j = i - 2; j >= 4; j -= 2) {
                dp[i] += dp[i-j] * 2;
            }
        }

        System.out.println(dp[n]);
    }
}

참고: https://velog.io/@newtownboy/JAVA2133%EB%B2%88-%ED%83%80%EC%9D%BC-%EC%B1%84%EC%9A%B0%EA%B8%B0

---

7) 2225번: 합분해 (골드 5)

• 문제 요약: 0부터 N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수를 구하는 프로그램을 작성하시오. 덧셈의 순서가 바뀐 경우는 다른 경우로 센다(1+2와 2+1은 서로 다른 경우). 또한 한 개의 수를 여러 번 쓸 수도 있다. 결과는 1,000,000,000으로 나눈 나머지.
  

---

문제 풀이

먼저 작은 값을 일일히 대입해보면서 감을 잡는 방법으로 진행했다.

• N=1 일 때
  • K=1: 1가지 (1)
  • K=2: 2가지 (1+0, 0+1)
  • K=3: 3가지 (0+1+0, 1+0+0, 0+0+1)
• N=2 일 때
  • K=1: 1가지 (2)
  • K=2: 3가지 (2+0, 0+2, 1+1)
  • K=3: 6가지 (2+0+0, 0+2+0, 0+0+2, 0+1+1, 1+0+1, 1+1+0)
• N=3 일 때
  • K=1: 1가지 (3)
  • K=2: 4가지 (3+0, 0+3, 2+1, 1+2)
  • K=3: 10가지 (3+0+0, 0+3+0, 0+0+3, 1+1+1, 2+0+1, 1+0+2, 0+1+2, 0+2+1, 1+2+0, 2+1+0)

이 패턴에서 바로 점화식이 나온다:

dp[n][k] = dp[n-1][k] + dp[n][k-1]

• 마지막에 더한 값을 1 증가시키는 경우(n-1, k)와
• 항의 개수를 늘려서 같은 합을 만드는 경우(n, k-1)의 합.

2) 점화식/기저값 정리 (내 코드 기준)

• dp[n][k] = 합이 n이 되도록 k개 수로 만드는 방법 수
• 기저값
  • dp[n][1] = 1 (하나로 n을 만드는 방법은 n 하나뿐)
  • dp[1][k] = k (1을 k개로 만드는 방법은 k가지)
  • dp[n][0] = 0 (항이 0개면 양의 합은 만들 수 없음)
• 점화식

  dp[n][k] = (dp[n-1][k] + dp[n][k-1]) % MOD

---

1. 입출력/초기화

int[][] dp = new int[N + 1][K + 1];
for (int i = 0; i <= N; i++) {
    dp[i][0] = 0;
    dp[i][1] = 1;
}
for (int i = 0; i <= K; i++) {
    dp[1][i] = i;
}

• dp[i][1]=1, dp[1][i]=i 두 줄로 N=1, K=1 축의 기저를 고정.
• dp[i][0]=0으로 항 0개는 불가능하게 처리.

2. 점화식과 반복

for (int i = 2; i <= N; i++) {
    for (int j = 2; j <= K; j++) {
        dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % MOD;
    }
}

---

전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

    static int N;
    static int K;

    static int MOD = 1_000_000_000;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        K = Integer.parseInt(st.nextToken());

        int result = countWaysToSum();
        System.out.println(result);
    }

    public static int countWaysToSum() {
        int[][] dp = new int[N + 1][K + 1];
        for (int i = 0; i <= N; i++) {
            dp[i][0] = 0;
            dp[i][1] = 1;
        }

        for (int i = 0; i <= K; i++) {
            dp[1][i] = i;
        }

        for (int i = 2; i <= N; i++) {
            for (int j = 2; j <= K; j++) {
                dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % MOD;
            }
        }

        return dp[N][K];
    }
}

참고: https://superohinsung.tistory.com/293

---

8) 9465번: 스티커 (실버 1)

• 문제 요약: 2×N 스티커에서 인접(상하좌우)한 스티커는 동시에 뗄 수 없다. 점수가 적힌 스티커들을 골라 최대 점수를 구한다. 테스트 케이스가 여러 개.
  

---

문제 풀이

1) 처음에 주목한 점

• 같은 열에서 윗줄과 아랫줄은 서로 인접(세로) → 한 열에서 둘 다 선택 불가.
• 같은 줄에서 옆 칸(왼/오)은 인접(가로) → 같은 줄에서는 연속해서 붙어 있는 열을 동시에 선택 불가.
• 결국 열(column) 단위로 보면서, i열에서 윗줄을 고르면 직전(i-1)은 아랫줄만 가능, i-2는 양쪽 줄 모두에서 가능.

2) 점화식 도출

• 정의 dp[0][i] = i열의 윗 스티커를 선택했을 때 얻을 수 있는 최대 점수 dp[1][i] = i열의 아랫 스티커를 선택했을 때 얻을 수 있는 최대 점수
  
• 초기값

  dp[0][0] = sticker[0][0]
  dp[1][0] = sticker[1][0]
  n > 1 일 때
  dp[0][1] = dp[1][0] + sticker[0][1]
  dp[1][1] = dp[0][0] + sticker[1][1]

• 전개(i ≥ 2)

  dp[0][i] = max(dp[1][i-1], dp[1][i-2]) + sticker[0][i]
  dp[1][i] = max(dp[0][i-1], dp[0][i-2]) + sticker[1][i]
  

  • i열 윗줄을 고르면, i-1에서는 아랫줄만 가능, i-2에서는 아랫줄 선택으로 끝난 상태와 이어 붙이는 게 안전하므로 dp[1][i-2]까지 비교.
    
  • 아랫줄도 대칭.
• 정답 마지막 열에서 둘 중 큰 값:

  answer = max(dp[0][n-1], dp[1][n-1])
  

---

1. 입출력/초기화 (내 코드 흐름)

int t = Integer.parseInt(br.readLine());
while (t-- > 0) {
    int n = Integer.parseInt(br.readLine());
    int[][] sticker = new int[2][n];
    int[][] dp = new int[2][n];

    // 입력
    ...
    // 초기값
    dp[0][0] = sticker[0][0];
    dp[1][0] = sticker[1][0];
    if (n > 1) {
        dp[0][1] = dp[1][0] + sticker[0][1];
        dp[1][1] = dp[0][0] + sticker[1][1];
    }

• n=1일 때는 초기값만으로 처리되고 바로 답을 낸다.

2. 점화식과 반복

for (int i = 2; i < n; i++) {
    dp[0][i] = Math.max(dp[1][i - 1], dp[1][i - 2]) + sticker[0][i];
    dp[1][i] = Math.max(dp[0][i - 1], dp[0][i - 2]) + sticker[1][i];
}
int maxScore = Math.max(dp[0][n - 1], dp[1][n - 1]);

• 열을 왼쪽→오른쪽으로 진행하면서 “교차 선택 + 두 칸 전”만 비교하면 된다.

전체 코드 (내 코드)

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int t = Integer.parseInt(br.readLine());

        StringBuilder sb = new StringBuilder();
        while (t-- > 0) {
            int n = Integer.parseInt(br.readLine());
            int[][] sticker = new int[2][n];
            int[][] dp = new int[2][n];

            // 입력
            for (int i = 0; i < 2; i++) {
                StringTokenizer st = new StringTokenizer(br.readLine());
                for (int j = 0; j < n; j++) {
                    sticker[i][j] = Integer.parseInt(st.nextToken());
                }
            }

            dp[0][0] = sticker[0][0];
            dp[1][0] = sticker[1][0];

            if (n > 1) {
                dp[0][1] = dp[1][0] + sticker[0][1];
                dp[1][1] = dp[0][0] + sticker[1][1];
            }

            // DP 진행
            for (int i = 2; i < n; i++) {
                dp[0][i] = Math.max(dp[1][i - 1], dp[1][i - 2]) + sticker[0][i];
                dp[1][i] = Math.max(dp[0][i - 1], dp[0][i - 2]) + sticker[1][i];
            }

            int maxScore = Math.max(dp[0][n - 1], dp[1][n - 1]);
            sb.append(maxScore).append("\n");
        }
        System.out.print(sb);
    }
}

참고: https://velog.io/@yanghl98/%EB%B0%B1%EC%A4%80-9465-%EC%8A%A4%ED%8B%B0%EC%BB%A4-JAVA

---

9) 10844 - 쉬운 계단 수 (실버 1)

• 문제 요약

인접한 모든 자리의 차이가 1인 수를 계단 수라고 한다.

N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.

첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.

첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.

---

문제 풀이

1) 처음 주목한 점

• 첫 자릿수는 0 불가 → 시작 자릿값은 1~9만 가능.
• 인접 자릿수 차이 = 1 → 자릿값 d의 이웃은 d-1 또는 d+1.
• 경계값 처리: d=0이면 이웃은 1만, d=9이면 8만 가능.
• 길이(len)를 1씩 늘리며 마지막 자릿수 기준 DP로 전이하는 구조가 자연스럽다.

2) 점화식 도출

• 상태 정의: dp[len][d] = 길이 len에서 *마지막 자릿수가 d인 계단 수의 개수.
• 전이 논리: 길이가 하나 늘어날 때 마지막 자릿수 d는 이전 길이의 d-1 또는 d+1에서만 올 수 있음(경계 0↔1, 9↔8).
• 모듈러 적용: 각 합산마다 MOD=1,000,000,000으로 나머지 처리.

---

1) 초기값

• dp[1][1..9] = 1, dp[1][0] = 0 (선행 0 금지)

2) 점화식

• d = 0 → dp[len][0] = dp[len-1][1]
• d = 9 → dp[len][9] = dp[len-1][8]
• 1 ≤ d ≤ 8 → dp[len][d] = dp[len-1][d-1] + dp[len-1][d+1]
• 각 항은 매번 % MOD 처리

전체 코드

import java.io.*;
import java.util.*;

public class Main {
    static final long MOD = 1_000_000_000L;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());

        long[] prev = new long[10];
        for (int d = 1; d <= 9; d++) prev[d] = 1;  // dp[1][1..9] = 1

        for (int len = 2; len <= N; len++) {
            long[] cur = new long[10];
            cur[0] = prev[1] % MOD;
            for (int d = 1; d <= 8; d++) {
                cur[d] = (prev[d - 1] + prev[d + 1]) % MOD;
            }
            cur[9] = prev[8] % MOD;
            prev = cur;
        }

        long ans = 0;
        for (int d = 0; d <= 9; d++) ans = (ans + prev[d]) % MOD;
        if (N == 1) ans = 9; // dp[1] 합은 1..9의 9개
        System.out.println(ans % MOD);
    }
}

참고: https://st-lab.tistory.com/134