Algorithm Study : 2weeks - 분할 정복 알고리즘

정지인·2025년 9월 15일

[분할 정복 알고리즘 - Divide and Conquer Algorithm] 이란 ?

주어진 문제의 입력을 분할하여 문제를 해결(정복)하는 방식의 알고리즘
- 분할한 입력에 대하여 동일한 알고리즘을 적용하여 해를 계산
- 이들의 해를 취합하여 원래 문제의 해를 얻음
부분 문제와 부분 해
- 분할된 입력에 대한 문제를 부분 문제 (subproblem)
- 부분 문제의 해를 부분 해
- 부분 문제는 더 이상 분할할 수 없을 때까지 분할

참고: https://olrlobt.tistory.com/45

[분할 정복 알고리즘과 DP의 차이점]

분할정복 알고리즘과 동적 계획법은 모두 대규모 문제를 해결하기 위한 알고리즘
한 문제를 작게 나눈다는 점에서 유사한 접근 방법을 가지고 있다. 하지만, 목적과 사용 방법에 분명한 차이가 있다.
분할정복:
- 문제를 작게 나누어 해결하고, 이 해결을 결합하여 원래의 문제를 해결.
- 재귀를 이용하여 구현 (부분 문제들이 서로 독립적일 때 사용하기 좋다.)
- 예) 정렬 알고리즘인 합병 정렬(Merge Sort)은 분할정복 알고리즘을 이용하여 구현.
동적 계획법(DP)
- 하위 문제들을 한 번씩만 계산, 이를 이용하여 상위 문제를 효율적으로 계산하는 것에 목적을 둔다.
- 반복문을 이용하여 구현하는 것이 일반적 (부분 문제들이 서로 종속적일 때 사용하기 좋다.)
- 예) 최단 경로 문제는 동적 계획법을 이용하여 해결.

💡

문제의 특성에 따라 분할정복 알고리즘과 동적 계획법 중 적합한 알고리즘을 선택하여 사용하는 것이 중요하다.

[분할정복 알고리즘의 종류 및 탐색과정]

이 프로세스는 작게 분할한 문제가 직접 해결 가능할 만큼 충분히 작아질 때까지 재귀적으로 계속된다.

일반적으로 분할정복 알고리즘은 다음 세 단계로 구성된다.

합병 정렬 (Merge Sort)
퀵 정렬 (Quick Sort)
이진 탐색 (Binary search)
선택 문제 (Selection) 알고리즘
- 문제가 2개로 분할되나, 그 중에 1개의 부분 문제는 고려할 필요가
  없으며, 부분 문제의 크기가 일정하지 않은 크기로 감소하는 알고리즘
삽입 정렬, 피보나치 수의 계산
- 부분 문제의 크기가 1, 2개씩 감소하는 알고리즘

[분할 정복 설계]

분할(Divide): 문제를 작은 하위 문제로 분할.
정복(Conquer): 각 하위 문제는 재귀적(반복되는 패턴을 이용하여)으로 해결.
결합(Combine): 하위 문제의 해결책을 결합하여 원래 문제를 해결.

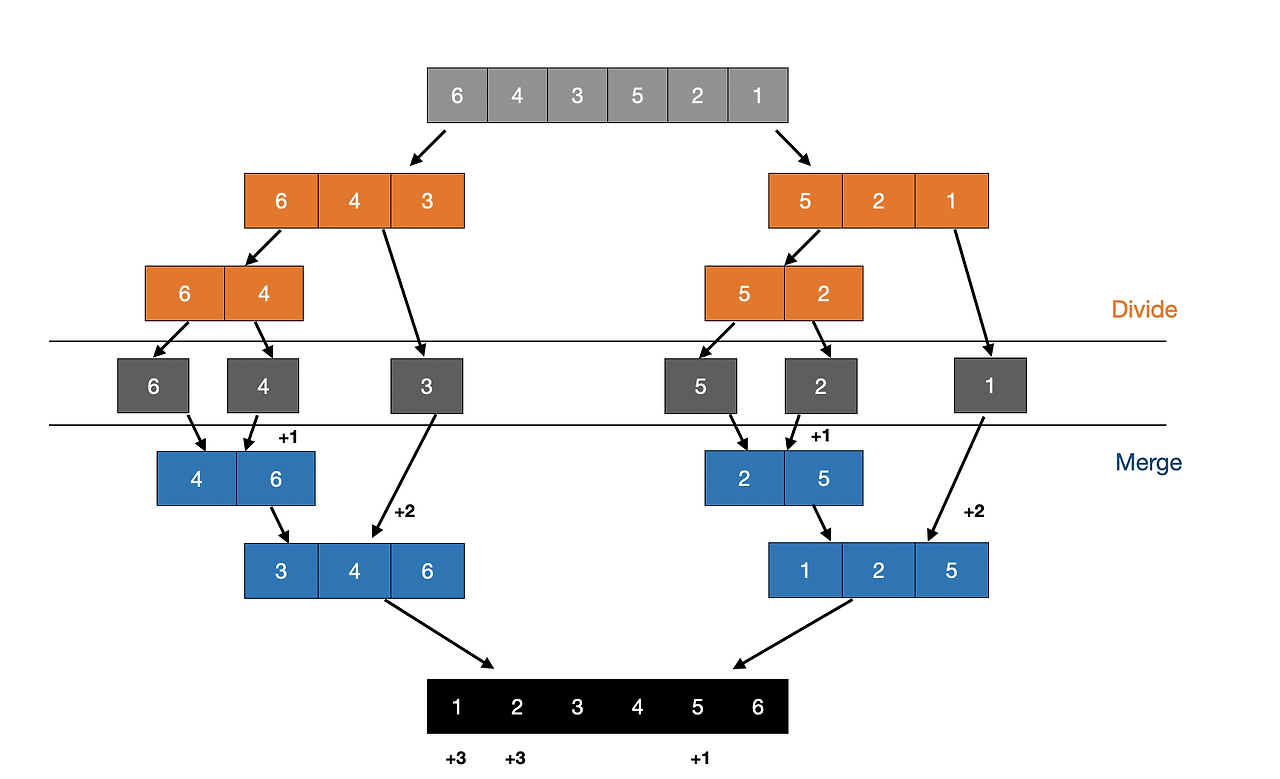
Divide를 제대로 나누면 Conquer과정은 자동으로 쉬워진다. 그래서 Divide를 잘 설계하는 것이 중요!
분할정복 알고리즘은 재귀 알고리즘이 많이 사용되는데, 이 부분에서 분할정복 알고리즘의 효율성을 깎아내릴 수 있다.

1. [합병 정렬 (Merge Sort) 알고리즘 동작 원리]

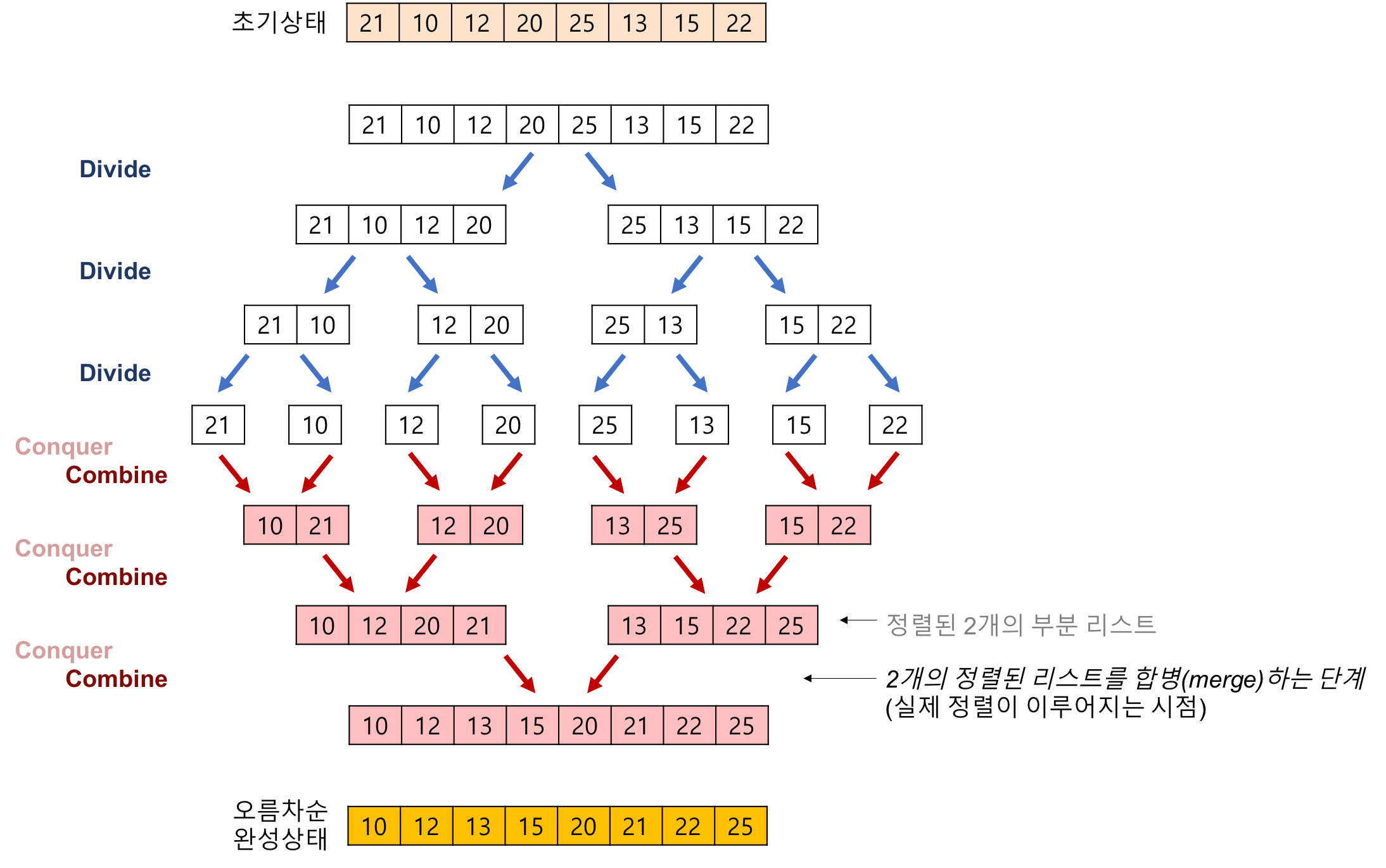
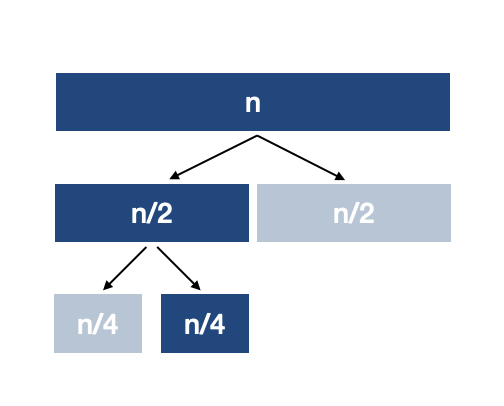
하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법.
- n개의 숫자들을 n/2개씩 2개의 부분 문제로 분할
- 각각의 부분 문제를 순환으로 합병 정렬
- 2개의 정렬된 부분을 합병하여 정렬(정복)
합병 과정이 문제를 정복하는 것

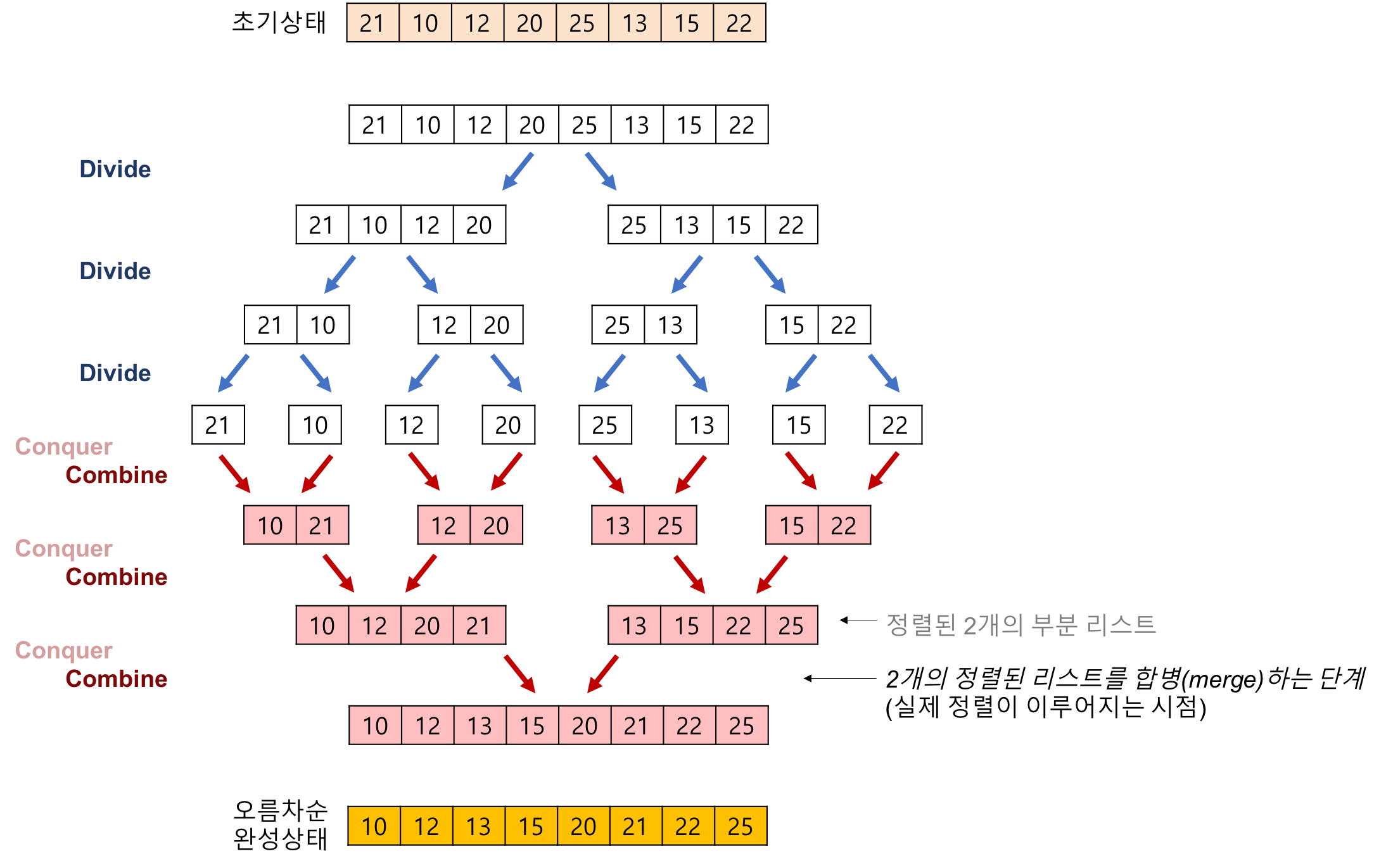
분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면(left<right) 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.

시간 복잡도

분할 단계: 중간 인덱스 계산 + 두 번 재귀 호출 준비 → O(1)
합병 단계: 정렬된 길이 m, n 배열 합치기 → 최대 비교 횟수: m + n − 1 → 시간: O(m + n)
층수(레벨): 크기 n을 1이 될 때까지 2로 나눔 → log₂ n
레벨당 작업량: 모든 원소가 합병에 참여 → O(n)
전체 시간 복잡도: 레벨 수 × 레벨당 작업량 = O(n log n) (점화식: T(n) = 2T(n/2) + O(n) ⇒ T(n) = O(n log n))

간단한 구현

import java.util.Arrays;

public class Main {
    private static int[] tmp;

    public static void mergeSort(int[] a) {
        if (a == null || a.length < 2) return;
        tmp = new int[a.length];
        mergeSort(a, 0, a.length - 1);
    }

    private static void mergeSort(int[] a, int l, int r) {
        if (l >= r) return;
        int m = (l + r) >>> 1;      // (l+r)/2 overflow 방지
        mergeSort(a, l, m);
        mergeSort(a, m + 1, r);
        merge(a, l, m, r);
    }

    private static void merge(int[] a, int l, int m, int r) {
        int i = l, j = m + 1, k = l;
        while (i <= m && j <= r) {
            if (a[i] <= a[j]) tmp[k++] = a[i++];
            else              tmp[k++] = a[j++];
        }
        while (i <= m) tmp[k++] = a[i++];
        while (j <= r) tmp[k++] = a[j++];
        System.arraycopy(tmp, l, a, l, r - l + 1);
    }

    public static void main(String[] args) {
        int[] src = {1, 9, 8, 5, 4, 2, 3, 7, 6};
        mergeSort(src);
        System.out.println(Arrays.toString(src));
    }
}

출처:

https://yunmap.tistory.com/entry/알고리즘-Java로-구현하는-쉬운-Merge-Sort-병합-정렬-합병-정렬

[현미와 백미는 섞어먹자.:티스토리]

합병 정렬의 단점

대부분의 정렬 알고리즘들은 입력을 위한 메모리 공간과 O(1) 크기의 메모리 공간만을 사용하면서 정렬 수행
- O(1) 크기의 메모리 공간이란 입력 크기 n과 상관없는 크기의 공간(예를 들어, 변수, 인덱스 등)을 의미
합병 정렬의 공간 복잡도: O(n)
- 입력을 위한 메모리 공간 (입력 배열)외에 추가로 입력과 같은 크기의 공간 (임시 배열)이 별도로 필요.
- 2개의 정렬된 부분을 하나로 합병하기 위해, 합병된 결과를 저장할 곳이 필요하기 때문

2. [퀵 정렬 (Quick Sort) 알고리즘 동작 원리]

퀵 정렬은 분할 정복 알고리즘으로 분류
- 사실 알고리즘이 수행되는 과정을 살펴보면 정복 후 분할하는 알고리즘
퀵 정렬 알고리즘은 문제를 2개의 부분 문제로 분할
- 각 부분 문제의 크기가 일정하지 않은 형태의 분할 정복 알고리즘
퀵 정렬은 피봇(pivot)이라 일컫는 배열의 원소(숫자)를 기준으로 피봇보다 작은 숫자들은 왼편으로, 피봇보다 큰 숫자들은 오른편에 위치하도록 분할하고, 피봇을 그 사이에 놓는다.
- 퀵 정렬은 분할된 부분문제들에 대해서도 위와 동일한 과정을 순환으로 수행하여 정렬

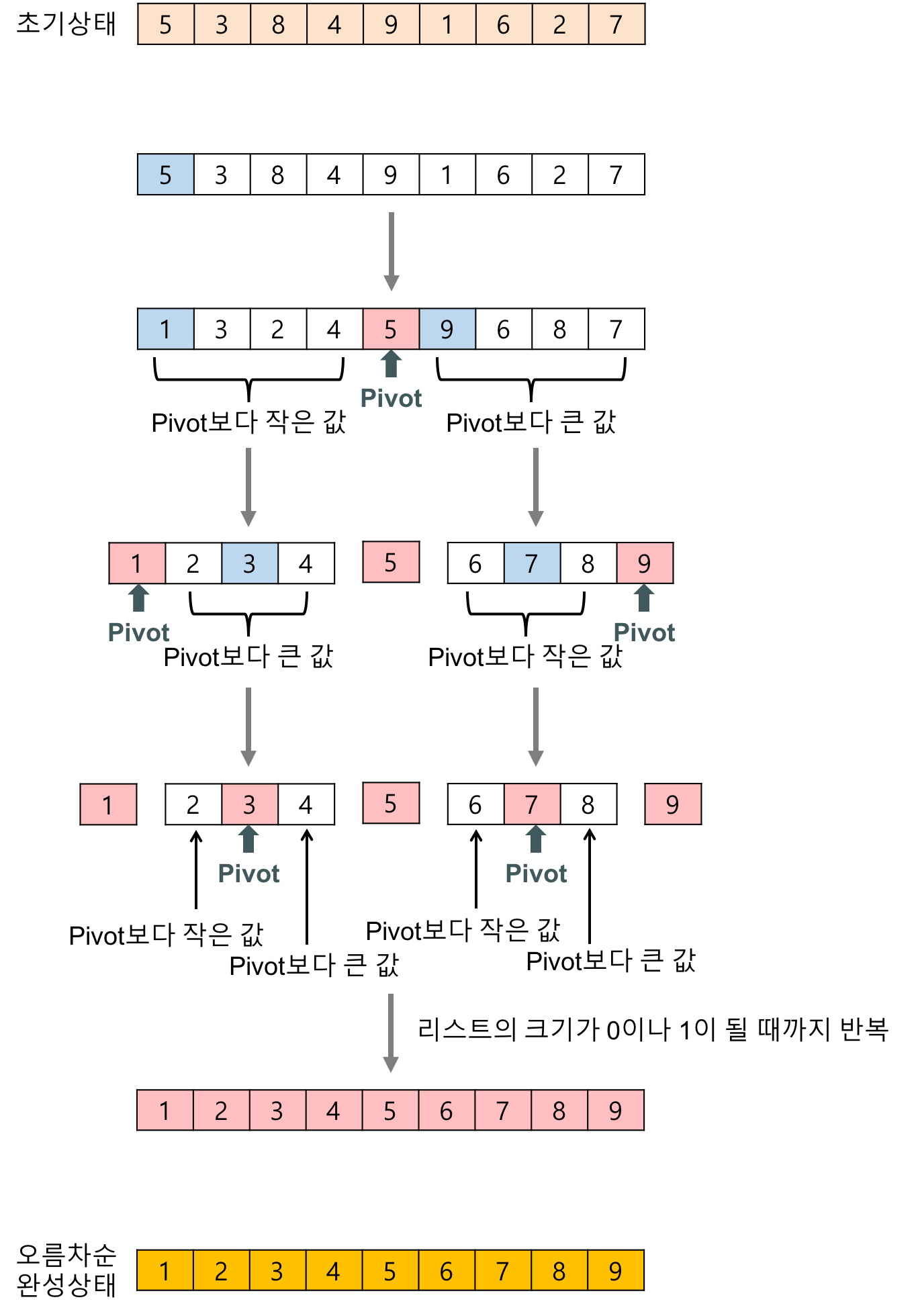
분할(Divide): 피봇 하나를 선택하여 피봇을 기준으로 2개의 부분 배열로 분할한다.
정복(Conquer): 피봇을 기준으로 피봇보다 큰 값, 혹은 작은 값을 찾는다. 왼쪽에서 부터 피봇보다 큰 값을 찾고 오른쪽에서 부터는 피봇보다 작은 값을 찾아서 두 원소를 교환한다. 분할된 부분 배열의 크기가 0이나 1일 될때까지 반복한다.
결합(Combine): conquer과정에서 값의 위치가 바뀌므로 따로 결합은 하지 않는다.

간단한 구현

import java.util.Arrays;

public class Main {
	public static void main(String[] args) {
		int[] arr = {3, 5, 2, 7, 1, 4, 6};
		int[] tmp = new int[arr.length];
		mergeSort(arr, tmp, 0, arr.length - 1);
		System.out.println("합병 정렬: " + Arrays.toString(arr));
}

	public static void mergeSort(int[] arr, int[] tmp, int left, int right) {
    if (left >= right) return;
    int mid = (left + right) >>> 1;
    mergeSort(arr, tmp, left, mid);
    mergeSort(arr, tmp, mid + 1, right);
    merge(arr, tmp, left, mid, right);
}

	private static void merge(int[] arr, int[] tmp, int left, int mid, int right) {
    int i = left, j = mid + 1, k = left;

    // 두 포인터로 병합 (안정성: 왼쪽 <= 오른쪽이면 왼쪽 먼저)
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) tmp[k++] = arr[i++];   // stable
        else                 tmp[k++] = arr[j++];
    }
    while (i <= mid)  tmp[k++] = arr[i++];
    while (j <= right) tmp[k++] = arr[j++];

    System.arraycopy(tmp, left, arr, left, right - left + 1);
}

}

퀵 정렬(Quick Sort) 성능 요약

핵심: 피봇 선택 품질이 성능을 좌우함. 극단(최소/최대) 피봇이면 한쪽으로 치우친 분할 발생.
최악(Worst) 경우: 피봇이 매번 최소(또는 최대) → 비교 횟수 합이 n-1 + n-2 + … + 1 = n(n-1)/2 → O(n²)
최선(Best) 경우: 매 단계에서 반씩 균등 분할 → 각 층 비교 O(n) × 층수 log₂n → O(n log n)
평균(Average) 경우: 피봇을 무작위로 고른다고 가정하면, 기대 성능은 최선과 동일하게 O(n log n)
근거 요약:
- 층별 비용은 항상 입력 크기에 비례(O(n)).
- 균등 분할이면 층수는 log₂n, 편향 분할이면 층수가 n에 가까워져 O(n²)로 악화.

추가: 퀵 정렬: 피봇 선정 & 성능 향상 요약

피봇 선정 방법

랜덤 피봇: 무작위로 하나 선택 → 평균적으로 균형 잡힌 분할 기대.
Median-of-Three: 왼쪽/중간/오른쪽 3개 중 중앙값을 피봇으로 선택 → 이미 정렬되었거나 역정렬된 입력에서 편향 완화.
- 예: [31, 1, 26] → 중앙값 26을 피봇.
Tukey’s Ninther(“세 개의 세 중 중앙값”): 배열을 3구간으로 잡고, 각 구간에서 (왼/중/오) 3개 중 중앙값을 구한 뒤, 그 3개 중앙값의 중앙값을 피봇으로 사용 → 극단적 편향 가능성을 더 낮춤.

성능 향상(하이브리드)

작은 구간은 삽입 정렬로 전환: 재귀 오버헤드가 커지는 작은 부분배열(예: 25~50 이하)에서는 더 이상 분할하지 않고 삽입 정렬 적용.
- 근거 부족/환경 의존: 임계값은 플랫폼·캐시·컴파일러 등에 따라 달라 실험적으로 정하는 것이 일반적입니다 (확실하지 않음: 고정 최적값은 없음).

복잡도 재정리

최악: 피봇이 매번 최소/최대 → O(n²)
평균/최선: 균등 분할 가정(또는 무작위 피봇 기대치) → O(n log n)

핵심 메시지: 좋은 피봇(중앙값 근처)을 선택하고, 작은 구간에서 삽입 정렬로 스위칭하면, 실제 실행 시간(상수항)이 유의하게 줄어든다.

3. [이진 탐색(Binary search) 알고리즘 동작 원리]

정렬된 데이터를 효과적으로 탐색할 수 있는 방법이다. (정렬된 데이터만 사용 가능; 참고로 정렬되지 않은 데이터 탐색은 파라메트릭 서치로 가능)

분할(Divide): 배열의 가운데 원소를 기준으로 왼쪽, 오른쪽 부분배열로 분할한다. 탐색키와 가운데 원소가 같으면 분할을 종료한다.
정복(Conquer): 탐색키가 가운데 원소보다 작으면 왼쪽 부분배열을 대상으로 이진 탐색을 순환 호출하고, 크면 오른쪽 부분배열을 대상으로 이진 탐색을 호출한다.
결합(Combine): 탐색 결과가 직접 반환되므로 결합이 불필요하다.

💡

[파라메트릭 서치 (이분탐색)] 란 ?

최적화 문제를 결정 문제로 바꾸어 해결하는 기법이다. 결정 문제란, '예' 혹은 '아니오'로 답하는 문제를 말한다. '주어진 범위에서 원하는 조건을 만족하는 가장 알맞은 값을 찾는 문제'에 주로 파라메트릭 서치를 사용한다.

간단한 구현

반복문을 이용한 방법

int binarySearch (int arr[], int low, int high, int key) {
  while (low <= high) {
    int mid = low + (high-low) / 2;

    if (arr[mid] == key) // 종료 조건1 검색 성공.
      return mid;
    else if (arr[mid] > key)
      high = mid - 1;
    else
      low = mid + 1;
  }
  return -1 ; // 종료 조건2 (low > high) 검색 실패.
}

재귀 함수를 이용한 방법

int binarySearch (int arr[], int low, int high, int key) {

  if (low > high) // 종료 조건2 검색 실패.
    return -1;

  int mid = low + (high-low)/2;

  if (arr[mid] == key) // 종료 조건1 검색 성공.
    return mid;
  else if (arr[mid] > key)
    return binarySearch(arr, low, mid-1, key);
  else
    return binarySearch(arr, mid+1, high, key);
}

추가: [삽입 정렬 - Insertion Sort]

자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘.
정렬되지 않은 목록(리스트, 배열)을 정렬된 부분과 정렬되지 않은 부분으로 나누며 정렬되지 않은 부분의 원소를 하나씩 선택하여 정렬된 부분의 적절한 위치에 삽입하는 방식으로 동작.

간단한 구현

package io.github.ones1kk.study.sorting;

public class InsertionSort {

    public static void insertionSort(int[] arr, int size) {
        for (int i = 1; i < size; i++) {
            int target = arr[i];

            int j = i - 1;
            while (j >= 0 && target < arr[j]) {
                arr[j + 1] = arr[j];
                j--;
            }

            arr[j + 1] = target;
        }
    }

}

[분할정복 특징 및 장단점]

분할된 작은 문제는 원래 문제와 성격이 동일하다 -> 입력 크기만 작아짐
분할된 문제는 서로 독립적이다(중복 제거 X) -> 순환적 분할 및 결과 결합 가능

분할정복은 Top-down방식으로 재귀 호출의 장단점과 똑같다고 보면 된다.

분할정복 알고리즘 장점:

빠른 속도: 큰 문제를 작은 하위 문제로 분할하고 해결하여 전체 문제를 해결하는 데 걸리는 시간을 줄일 수 있다.
쉬운 병렬화: 분할정복 알고리즘은 하위 문제를 병렬로 처리하기 쉬우므로 멀티코어 시스템에서 성능을 크게 향상할 수 있다.
유연성: 이 알고리즘은 여러 응용 분야에서 사용될 수 있으며, 문제의 복잡도와 데이터 크기에 상관없이 적용할 수 있다.

분할정복 알고리즘 단점:

추가적인 메모리 요구: 알고리즘은 재귀적으로 호출되므로 많은 추가적인 메모리를 필요로 할 수 있다.
최악의 경우 시간 복잡도: 일부 문제에 대해서는 분할정복 알고리즘이 최악의 경우에도 빠른 해결책을 제공하지 못할 수 있다.
구현의 복잡성: 이 알고리즘은 구현이 비교적 복잡할 수 있으며, 종종 추가적인 문제를 발생시킬 수 있다.

분할정복 알고리즘은 많은 문제에 대해 매우 효과적이며, 많은 응용 분야에서 사용된다. 하지만 구현이 복잡하고 추가적인 메모리 요구가 있을 수 있으므로, 적용 전에 장단점을 고려해야 한다.

장점	단점
Top-down 재귀방식으로 구현하기 때문에 코드가 직관적.	재귀 함수 호츨로 오버헤드가 발생할 수 있다.
문제를 나누어 해결한다는 특징상 병렬적으로 문제를 해결할 수 있다.	∙ 스택에 다량의 데이터가 보관되는 경우 오버플로우가 발생할 수 있다.

참고:
https://loosie.tistory.com/237

https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html

[직접 풀어보며 이해하기]

난이도 별로 한 문제씩 준비해봤다. 브론즈로 먼저 분할 정복 알고리즘이 어떤 느낌인 지 익히고, 실버 문제로 직접 알고리즘을 문제에 적용 시키는 연습을 한 후 골드 문제로 심화과정을 익혀보도록 하겠다.

1) Bronze : 백준 13277번

https://www.acmicpc.net/problem/13277

백준에서 분할 정복으로 분류된 유일한 브론즈 문제이다 !

브론즈 문제가 이 문제 뿐이라 가져오긴 했지만 굉장히 당황스럽다.

매우 간단한 문제이지만 …. 나는 틀리긴 했다 …

사실 이게 분할 정복 알고리즘이랑 무슨 연관인 지는 모르겠다 !!!

구현

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.math.BigInteger;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        BigInteger n = new BigInteger(st.nextToken());
        BigInteger m = new BigInteger(st.nextToken());

        System.out.println(n.multiply(m));

    }
}

2) Silver : 백준 2630번

https://www.acmicpc.net/problem/2630

이번에 풀어볼 문제는 2630의 색종이 문제이다 !!

이 문제를 풀 때는 흰색과 파란색 정사각형 색종이의 개수를 알아내야 하는데, 규칙은 이렇다.

부분 색종이는 모두 같은 색상이어야 한다.
만약 모두 같은 색상이 아닐 경우 색종이를 잘라야 한다.
색종이를 자를 때는 1/2 씩, 즉 절반씩 잘라서 정사각형을 얻어야 한다.

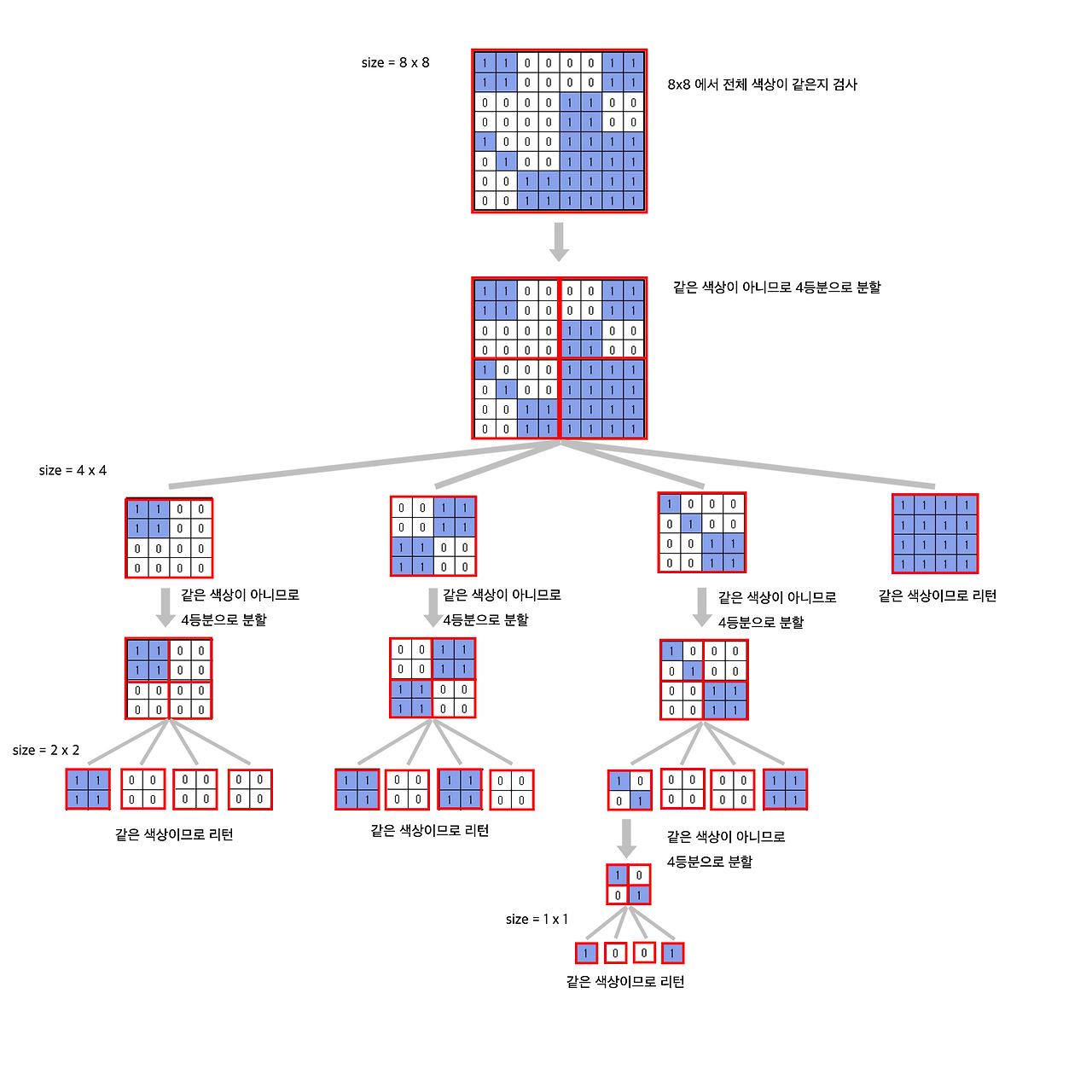
위의 조건대로 문제를 풀자면 이러한 그림의 형태를 얻을 수 있다!!

코드를 구성할 때 중요한 점은

각각의 행과 열의 시작점(초기는 (0, 0)이 기준)에서 현재 파티션에 대하여 모두 같은 색상인지 체크를 먼저 해야한다.
색상이 같다면 해당 색상의 개수를 1 증가시키고 함수를 종료한다.
색상이 같지 않다면, 4등분 하여 각 부분 문제로 쪼개어 문제를 푼다.

이러한 조건들로 코드를 구성하자면 다음과 같은 코드를 얻을 수 있다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
	
	static int white = 0;
	static int blue = 0;
	static int[][] paper;
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		paper = new int[N][N];
		StringTokenizer st;
		for(int i = 0; i < N; i++) {
			st = new StringTokenizer(br.readLine());
			for(int j = 0; j < N; j++) {
				paper[i][j] = Integer.parseInt(st.nextToken());
			}
		}
		divied(0, 0, N);
		System.out.println(white);
		System.out.println(blue);
	}
	
	public static void divied(int x, int y, int n) {
		boolean flag = true;
		// 색종이 통일 되어 있는지 탐색
		for(int i = 0; i < n; i++) {
			for(int j = 0; j < n; j++) {
				// 다른 색 하나 있을 경우
				if(paper[x][y] != paper[x + i][y + j]) {
					flag = false;
					break;
				}
				if(!flag) break;
			}
		}
		// 탐색한 영역이 한가지 색으로 통일된 경우
		if (flag) {
			if(paper[x][y] == 0) {
				white++;
			}else {
				blue++;
			}
		}else {
			divied(x, y, n / 2);
			divied(x + n / 2, y, n / 2);
			divied(x, y + n / 2, n / 2);
			divied(x + n / 2, y + n / 2, n / 2);
		}
	}
	
}

3) Gold : 백준 1074번

https://www.acmicpc.net/problem/1074

다음은 백준 골드5의 문제이다… 내 실력으론 혼자서 골드 문제를 풀 수 없다. 골드 5인만큼 난이도가 상당해서 같이 차근차근 풀어보는 것이 좋을 것 같아서 가져왔다!!

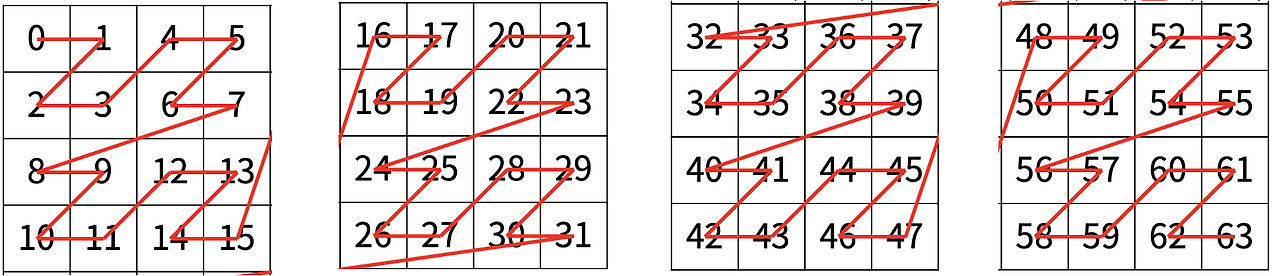
문제는 간단하게, Z 모양으로 반복되는 패턴에서,

0행 0열부터 시작한다면, 3행 3열은 몇 번째 숫자를 나타 내는지를 구하는 문제이다.

이 문제를 분할정복을 이용하여 해결하여 봅시다...

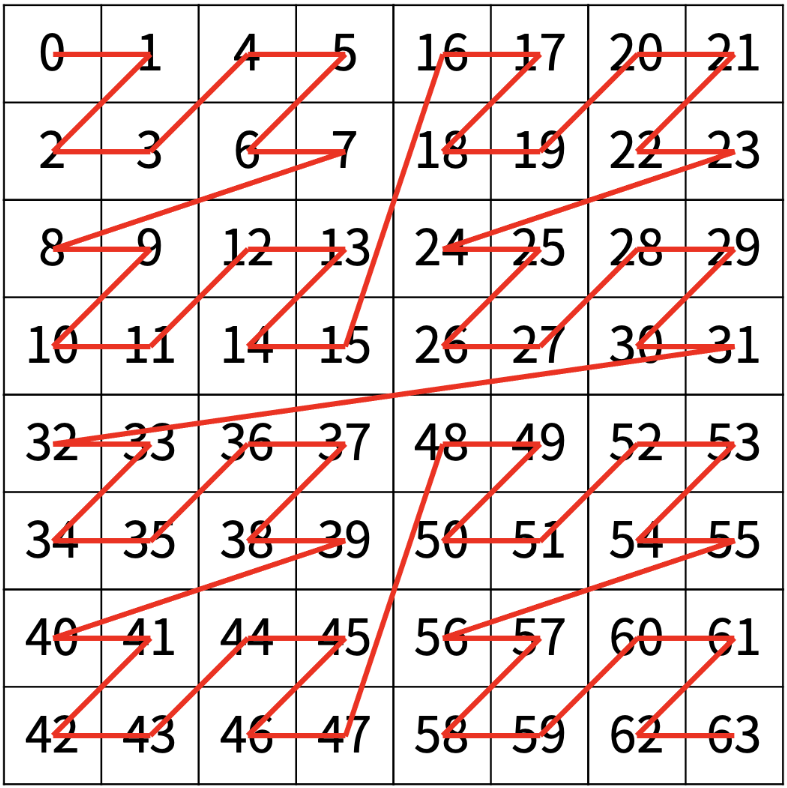
먼저, 처음에 해야할 것은 분할 단계이다 !!!

일단은 숫자는 신경 쓰지 말고 사각형의 크기에만 집중해 보자. 위의 그림은 반복되는 패턴이 있으므로 4 등분하여 문제를 작게 분할해보자.

이 중, 구하고자 하는 3행 3열은 첫 번째 사각형에 위치한다. 하지만 3행 3열에 집중하지 말고, 사각형에만 집중해 보자.

그리고 보면 이 사각형을 한 번 더 나눌 수 있을 것 같다 !! 아까와 같이 똑같이 반복되는 패턴 4개로 작게 분할 한다.

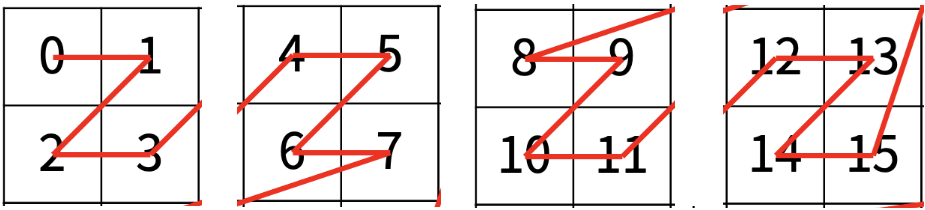
이 그림에서도 숫자가 아니라 사각형에 집중하자. 엥 !!!! 아니 이것도 뭔가 나눌 수 있을 것 같다 ?? 한 번만 더 나눠보자 !!!.

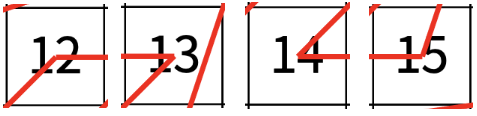
이제 더 이상 나눌 수 없을 것 같다 !! 이 것이 가장 작게 나눈 가장 작은 문제가 된다. 현재 그림에는 숫자가 쓰여 있어서 헷갈릴 수 있지만,

가장 작은 사각형 중에 네 번째 사각형이므로 실제 우리가 구한 값은 아래의 그림.

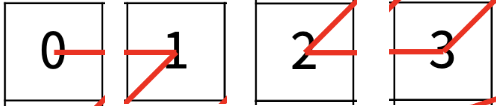
즉 해결 단계에서, 3의 값을 구한 것이다.

가장 작은 문제를 해결했으므로, 이제는 작은 문제들을 결합시킨다.

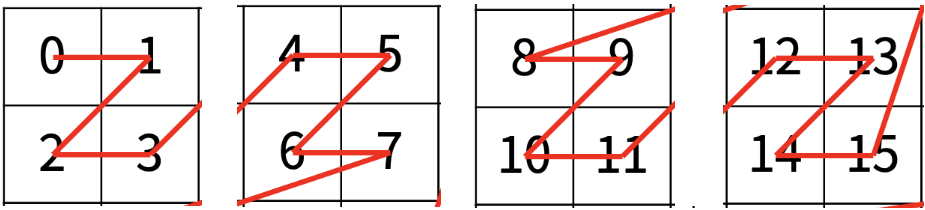
내가 구한 것은 가장 작은 문제에서 3의 값을 나타내지만, 이 작은 문제들의 결합인 위의 문제에서는 네 번째 그림을 나타낸다.

각 사각형의 첫 번째 값이 4 단위로 증가하기 때문에,

(가장 작은 사각형에서 구한 값 3) + (네 번째 사각형 4-1) x ( 단위 4) = 15의 값을 구할 수 있다.

마지막 위의 결합 부분에서는 구하고자 하는 결과가 첫 번째 사각형 이기 때문에, 그대로 15라는 답이 도출된다.

만약, 위 문제가 3행 3열이 아닌, 7행 3열을 구하는 문제였다면, 위 그림에서 세 번째 사각형에 위치한다.

각 사각형이 16 단위로 증가하기 때문에,

(이 전 사각형에서의 값 15) + ( 세 번째 사각형 3-1 ) x ( 단위 16) = 47의 값이 도출된다.

전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
	static int count = 0;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int r = Integer.parseInt(st.nextToken()); //행
		int c = Integer.parseInt(st.nextToken()); //열
		int size = (int) Math.pow(2, N); //한 변의 사이즈
		
		find(size, r, c);
		System.out.println(count);
	}

	private static void find(int size, int r, int c) {
		if(size == 1)
			return;
		
		if(r < size/2 && c < size/2) {
			find(size/2, r, c);
		}
		else if(r < size/2 && c >= size/2) {
			count += size * size / 4;
			find(size/2, r, c - size/2);
		}
		else if(r >= size/2 && c < size/2) {
			count += (size * size / 4) * 2;
			find(size/2, r - size/2, c);
		}
		else {
			count += (size * size / 4) * 3;
			find(size/2, r - size/2, c - size/2);
		}
	}
}

출처: https://wiselog.tistory.com/133

정지인

멋쟁이사자 13기 백엔드

이전 포스트

Algorithm Study : 1weeks - Dynamic Programing

다음 포스트

Algorithm Study : 2weeks - 분할 정복 알고리즘

[분할 정복 알고리즘 - Divide and Conquer Algorithm] 이란 ?

[분할 정복 알고리즘과 DP의 차이점]

[분할정복 알고리즘의 종류 및 탐색과정]

[분할 정복 설계]

1. [합병 정렬 (Merge Sort) 알고리즘 동작 원리]

시간 복잡도

간단한 구현

합병 정렬의 단점

2. [퀵 정렬 (Quick Sort) 알고리즘 동작 원리]

간단한 구현

퀵 정렬(Quick Sort) 성능 요약

추가: 퀵 정렬: 피봇 선정 & 성능 향상 요약

피봇 선정 방법

성능 향상(하이브리드)

복잡도 재정리

3. [이진 탐색(Binary search) 알고리즘 동작 원리]

간단한 구현

추가: [삽입 정렬 - Insertion Sort]

간단한 구현

[분할정복 특징 및 장단점]

[직접 풀어보며 이해하기]

1) Bronze : 백준 13277번

구현

2) Silver : 백준 2630번

3) Gold : 백준 1074번

먼저, 처음에 해야할 것은 분할 단계이다 !!!

전체 코드

Algorithm Study : 1weeks - Dynamic Programing

알고리즘 : Ch.01 First Step

0개의 댓글

Algorithm Study : 2weeks - 분할 정복 알고리즘

[분할 정복 알고리즘 - Divide and Conquer Algorithm] 이란 ?

[분할 정복 알고리즘과 DP의 차이점]

[분할정복 알고리즘의 종류 및 탐색과정]

[분할 정복 설계]

1. [합병 정렬 (Merge Sort) 알고리즘 동작 원리]

시간 복잡도

간단한 구현

합병 정렬의 단점

2. [퀵 정렬 (Quick Sort) **알고리즘 동작 원리]**

간단한 구현

퀵 정렬(Quick Sort) 성능 요약

추가: 퀵 정렬: 피봇 선정 & 성능 향상 요약

피봇 선정 방법

성능 향상(하이브리드)

복잡도 재정리

3. [이진 탐색(Binary search) 알고리즘 동작 원리]

간단한 구현

추가: [삽입 정렬 - **Insertion Sort]**

간단한 구현

[분할정복 특징 및 장단점]

[직접 풀어보며 이해하기]

1) Bronze : 백준 13277번

구현

2) Silver : 백준 2630번

3) Gold : 백준 1074번

먼저, 처음에 해야할 것은 분할 단계이다 !!!

전체 코드

Algorithm Study : 1weeks - Dynamic Programing

알고리즘 : Ch.01 First Step

0개의 댓글

2. [퀵 정렬 (Quick Sort) 알고리즘 동작 원리]

추가: [삽입 정렬 - Insertion Sort]