[정보통신산업진흥원] AI 웹개발 취업캠프 - 유데미 필수 강의 후기/기록 ([AICE 자격대비반] 인공지능(AI) 능력시험 AICE)-(2)
AI_Web_nipa

AI 모델링 하는 순서
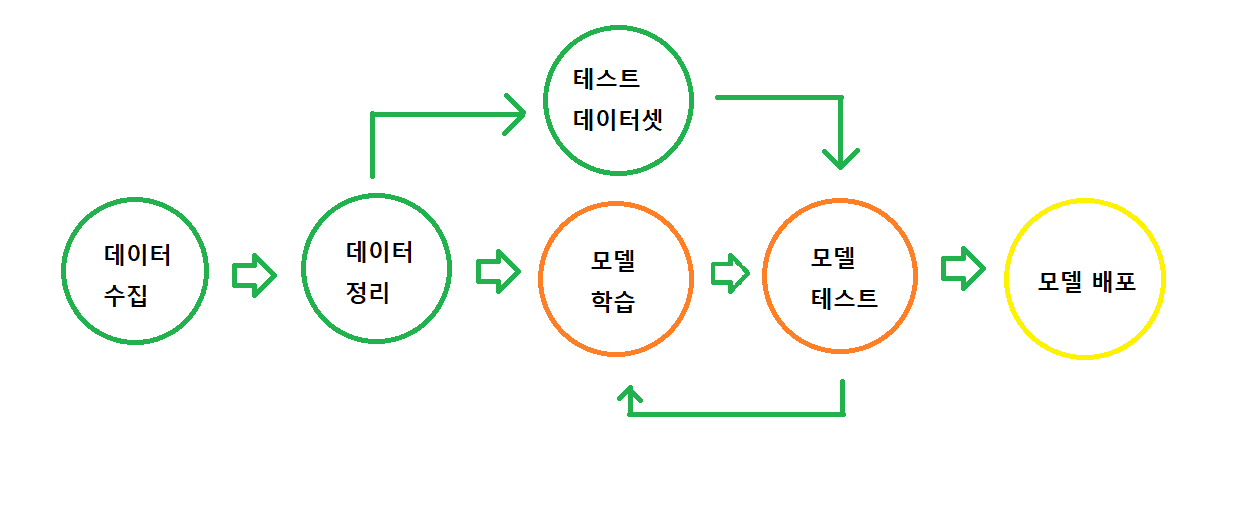
[데이터 분석 및 전처리하기]
1) 데이터시각화
데이터 자체 분석 vs 데이터 간 관계 분석
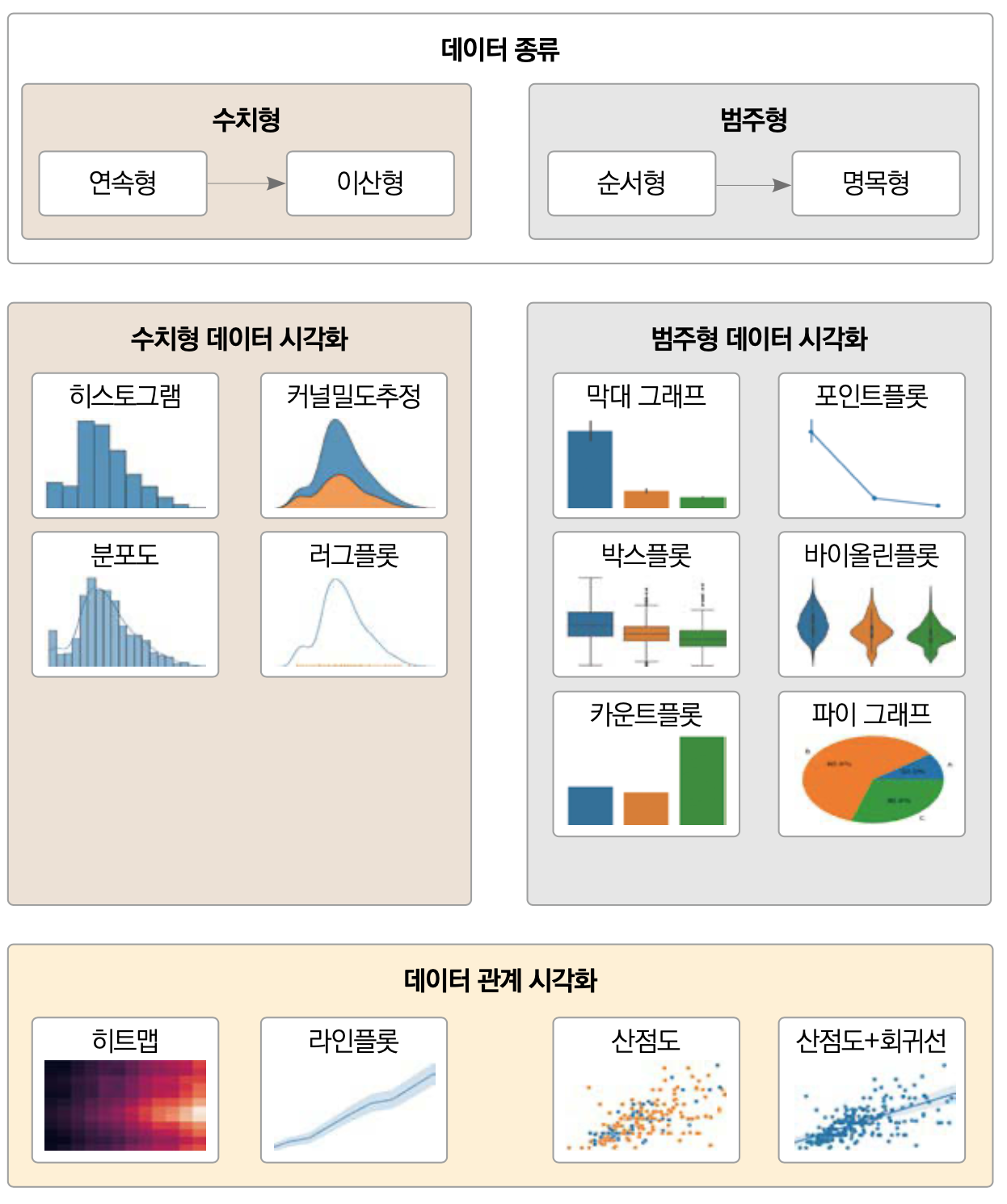
- EDA (Explorative Data Analysis) : 탐색적 데이터 분석 과정을 통해, Feature간의 연관관계 분석
Feature간 상관관계 분석 : scatter plot / Heat map
Feature 자체 분석 : Box plot / Dist plot
2) 결측치 처리
- 실무자 견해가 많이 반영되는 단계 : 분석 방향에 따라 결과에 차이
- 많은 시간이 투자되어야 함
- 데이터 현실을 반영한 처리 : 정확한 분석과 모델링 가능
제거(drop) : 가장 쉽게 처리할 수 있는 방법, 막대한 데이터 손실 동반
대체(fill) : 단순 대체할 경우, 전체적 통계 값에 영향
3) 이상치 처리
- 이상치 탐지(IQR) : 타겟 변수가 카테고리라면 카테고리 별 이상치 구분
- 이상치 처리 : 행 삭제, 다른 값으로 치환, 그대로 놔두기
4) 인코딩
카테고리 순서 여부에 따른 선택
Oridinal Encoding vs One-Hot Encoding
Ordinal Encoding (순서 인코딩): 범주형 변수의 값에 순서나 등급이 있을 때 사용됩니다. 즉, 범주 간에 상대적인 순서 또는 등급이 있는 경우에 적합합니다. 예를 들어, "낮음", "보통", "높음"과 같은 범주가 있을 때 이를 1, 2, 3과 같은 정수로 매핑하는 방법입니다.
장점:
간단하고 직관적인 방법입니다.
특히 범주의 순서가 중요한 경우, 해당 정보를 유지하면서 변환할 수 있습니다.
단점:
범주 간의 순서를 나타내기 위해 숫자를 사용하기 때문에, 모델은 이러한 값 사이에 일정한 간격이 있다고 오해할 수 있습니다. 이는 일반적으로 순서형 데이터에 적합하지만 명목형 데이터에는 부적절합니다.
One-Hot Encoding (원핫 인코딩): 범주형 변수를 이진 벡터로 변환합니다. 각 범주는 0 또는 1로 표현되며, 해당 범주에 속하는 인덱스는 1이고, 나머지 인덱스는 모두 0입니다. 이를 통해 범주 간의 상대적인 순서를 나타내지 않고 명목형 데이터를 처리할 수 있습니다.
장점:
범주 간의 순서를 고려하지 않고 명목형 데이터를 처리할 수 있습니다.
각 범주가 독립적으로 표현되므로 숫자 간의 오해를 방지합니다.
단점:
범주의 개수가 많을 경우, 인코딩된 벡터의 차원이 커져 메모리 사용량이 증가할 수 있습니다.
사용 사례: 성별("남성", "여성"), 도시("서울", "뉴욕", "도쿄")와 같이 범주 간의 순서가 중요하지 않은 데이터에 적합합니다.
4) 스케일링
컬럼 간 스케일 차이로 잘못된 판단을 할 여지가 있어 스케일링 적용
Min-Max Scaling vs Standard Scaling
Min-Max Scaling은 데이터를 일정 범위 내로 변환하는 방법 중 하나입니다. 주어진 데이터의 최솟값(Min)을 0으로, 최댓값(Max)을 1로 설정하여 모든 데이터를 이 새로운 범위에 매핑합니다.
장점:
데이터를 0과 1 사이로 압축하여 이상치에 민감하지 않습니다.
모든 특성을 동일한 스케일로 조정하기 때문에 일부 알고리즘에 도움이 됩니다.
단점:
이상치(outliers)가 있는 경우, 스케일링 후에도 여전히 이상치로 남을 수 있습니다.
데이터의 분포가 실제 분포와 다를 경우, 정보 손실이 발생할 수 있습니다.
사용 사례: 신경망 학습과 같이 입력 데이터의 스케일을 0과 1 사이로 조정해야 하는 경우.
Standard Scaling은 데이터를 평균이 0, 표준 편차가 1인 분포로 변환합니다. 각 데이터 포인트를 평균에서 뺀 다음, 표준 편차로 나누어 스케일링합니다.
장점:
이상치에 대한 영향을 줄이며, 데이터 분포의 형태를 유지합니다.
다양한 알고리즘 및 통계 분석에 적합합니다.
단점:
데이터 스케일링이 주요 분포를 크게 바꿀 수 있으므로, 종종 이상치를 다루는데 어려움을 겪을 수 있습니다.
사용 사례: 주성분 분석(PCA) 및 클러스터링과 같이 데이터 분포가 중요한 경우, 또는 이상치 처리가 필요한 경우.
어떤 것을 선택해야 할까?:
Min-Max Scaling은 데이터를 정해진 범위로 제한하고자 할 때 사용됩니다. 데이터가 이미 정규 분포를 따르고 있을 때 유용할 수 있습니다.
Standard Scaling은 데이터의 분포를 유지하면서 스케일링하고자 할 때 선택됩니다. 이상치가 있는 데이터에 대해 더 강력하며, 다양한 통계 및 머신 러닝 모델에 적용할 수 있습니다.
5) AI 모델링하기
모델 선택 및 학습 - 적절한 AI 알고리즘 선택을 위한 결정
"과제 목적이 예측인가?" vs "과제 목적이 설명인가"
- 모델 선택 및 학습 - 과대 적합 방지(조기종료 / 드롭아웃)
- 효율적 학습을 위한 학습 데이터 분리(학습 데이터 -> 미니배치) - 더 나은 모델 만들기 : 모델을 개선할 수 있는방법
[더 많은 수의 학습 데이터 사용, AI 알고리즘 변경, AI 알고리즘의 하이퍼파라미터 변경, 피처엔지니어링을 통한 파생 변수 생성]
Q. 필요한 데이터를 수집하고 전체적인 모습을 살펴 보았는데요. 어떻게 데이터를 분석하고 가공해야 성능 좋은 음원 흥행 가능성 예측 AI모델을 만들 수 있을까요?
A. 1. 시각화 분석 도구를 활용하여 데이터 분석을 해보자. 2. 통계 분석 도구를 활용하여 데이터 분석을 해보자. 3. 데이터 분석에서 얻은 인사이트로 데이터 가공을 해보자.
데이터 가공 - 결측치 처리->인코딩->스케일링
AI 모델링에서는 이런걸 고민해 봐요
- Linear Regression(머신러닝)
- Decision Tree(머신러닝)
- Random Forest(머신러닝)
- DNN(딥러닝)
더 많은 수의 학습 데이터 사용 / AI 알고리즘 변경 / 피처엔지니어링을 통한 파생 변수 생성 / AI 알고리즘의 하이퍼파라미터 변경
6) Model 학습 파라미터 설정
Optimizer : Loss 함수의 최적의 Gradient값을 찾는 알고리즘
ADAM (Adaptive Momentum) : 기존 방향이 이동하던 방향대로 관성에 따라 Step을 이동(Momentum) + 각 Feature별 기울기의 개선정도를 반영하여 이동하는 Step의 크기를 보정(Adaptive)
SGD (Stochastic GD) : Loss Gradient 계산 시, 전체 Data에 대해 Gradient를 계산하는 것이 아닌 Mini batch Data에 대해 Gradient를 계산하여 빠르게 Gradient를 계산, 최적의 Loss 획득
7) AI 과제 유형별 성능평가 지표
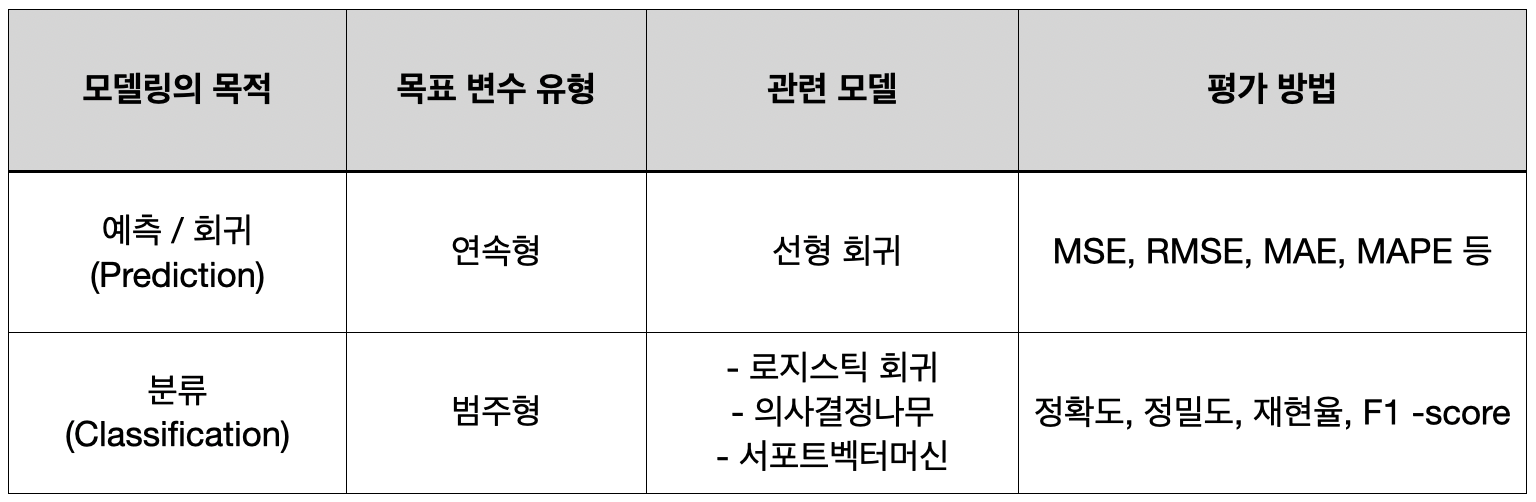
➰ MSE(Mean Squared Error : 평균 제곱 오차)
: 실제값과 예측값의 차이를 제곱해 평균한 것
➰ MAE(Mean Absolute Error : 평균 절대 오차)
: 실제 값과 예측값의 차이를 절댓값으로 변환해 평균한 것
정확도(Accuarcy)
정확도는 '전체 데이터중에, 정확하게 예측한 데이터의 수'라고 할 수 있다. 하지만 정확도를 분류 모델의 평가 지표로 사용할 때는 주의해야 하는데, 특히 불균형한 데이터(imbalanced data)의 경우에 정확도는 적합한 평가지표가 아니다.
정밀도(Precision)
정밀도는 '양성으로 판단한 것 중, 진짜 양성의 비율'이다.
정밀도 = TP / TP + FP
재현율(Recall) = 민감도(Sensitivity)
재현율은 '진짜 양성인 것들 중에서, 올바르게 양성으로 판단한 비율'이다. 양성 결과를 정확히 예측하는 능력으로, 모델의 완정 성을 평가하는 지표로 사용된다.
재현율 = TP / TP + FN
정밀도와 재현율은 Positive 데이터 세트의 예측 성능에 좀 더 초점을 맞춘 평가 지표이며, 이진 분류 모델의 업무 특성에 따라 특정 평가 지표가 더 중요한 지표로 간주될 수 있다. 예를 들어 재현율은 실제 Positive(양성)인 데이터 예측을 Negative로 잘못 판단하게 되면 업무 상 큰 영향이 발생하는 경우 더 중요한 지표로 간주되고, 정밀도는 실제 Negative(음성)인 데이터를 Positive로 잘못 판단하게 되었을 때 큰 문제가 발생되는 경우 더 중요한 지표로 간주된다.
재현율과 정밀도 모두 TP(True Positive)를 높이는데 초점을 맞추지만, 재현율은 FN(실제 Positive 한 것을 negative로 예측)한 것을 낮추는데, 정밀도는 FP를 낮추는데 초점을 맞춘다. 이와 같은 특성 때문에 재현율과 정밀도는 서로 보완적인 지표로 분류 성능을 평가하는 데 사용되는데, 이때 어느 한쪽을 강제로 높이면 다른 하나의 수치는 떨어지기 쉬워진다. 이를 정밀도/ 재현율은 트레이트 오프(Trade-off) 관계에 있다고 한다.
