[Algorithm] MST 1 - Kruskal

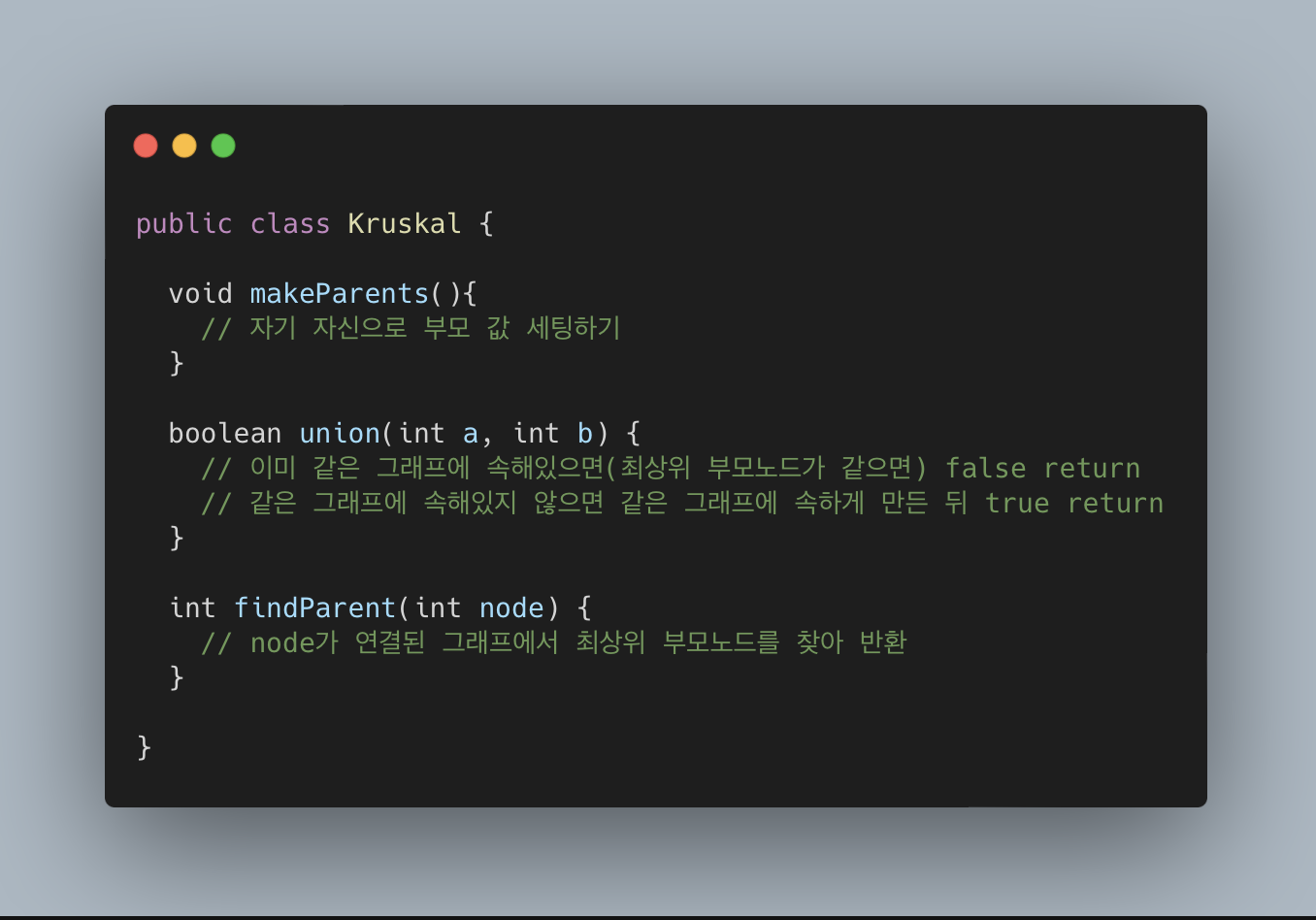
Kruskal 알고리즘

• 최소신장트리를 찾는 알고리즘 중 하나이다.

  최소신장트리(Minimum Spanning Tree): 전체 그래프를 연결하기 위한 최소 가중치의 합
  다익스트라: 한 정점에서 다른 정점까지 도착하기 위한 최소 거리

• 각 노드 사이의 거리가 양수일 때 사용한다.

• Union, Find를 사용한다 (각기 다른 두 노드를 하나의 그래프로 합치는 알고리즘)

• 노드의 수가 많지 않을 때 사용하는 것이 유리하다.

  Why?
  Kruskal은 간선의 가중치를 Sorting 하는 단계를 거친다. 이 때, Sorting의 최악의 시간복잡도는 O(NlogN)인데, 간선의 수가 너무 많으면 정렬하는데 시간이 오래걸려 Prim 알고리즘이 유리할 수 있다. Prim 알고리즘은 한 정점을 기준으로 최소 거리를 찾아나가는 알고리즘이기 때문에 따로 Sorting이 필요없어 간선의 수가 많을 때 사용한다.

1) 단계

1. 에지를 리스트에 담아 거리 순으로 오름차순 정렬한다.
2. 정렬된 에지리스트에서 연결된 노드들을 하나의 집합으로 합치며 거리를 더한다.
3. 모든 노드들이 하나의 그래프로 연결되면 집합으로 합치는 것을 멈추고 더한 거리를 반환한다.

   자세한 내용은 코드로 확인하세요!

2) 코드

코드를 입력하세요import java.util.*;
import java.io.*;

/**
 * Kruskal 알고리즘
 * - 최소 신장 트리
 * - 각 노드 사이의 거리가 양수일 때 사용
 * - Union, Find 사용
 * - 간선의 수가 적을 때 사용하는 것이 유리: Sorting이 들어가기 때문 - Sorting의 최대 시간복잡도 (O(NlogN))
 */

public class Kruskal {
    static int N, parents[];
    static Edge[] edgeList;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer stk = new StringTokenizer(br.readLine());
        N = Integer.parseInt(stk.nextToken());
        int E = Integer.parseInt(stk.nextToken());
        edgeList = new Edge[E];

        for (int i = 0; i < E; i++) {
            stk = new StringTokenizer(br.readLine(), " ");
            int from = Integer.parseInt(stk.nextToken());
            int to = Integer.parseInt(stk.nextToken());
            int weight = Integer.parseInt(stk.nextToken());
            edgeList[i] = new Edge(from, to, weight);
        }
        Arrays.sort(edgeList); // 간선 비용의 오름차순
        makeSet(); // 자기자신으로 부모 노드 세팅해놓기

        int result = 0, cnt = 0;
        for(Edge edge: edgeList) {
            if(union(edge.from, edge.to)) {
                result += edge.weight; // 최소 비용부터 더하게 될 것이기 때문
                if(++cnt == N-1) // 모든 노드들이 포함되어있을 경우 더이상 합칠 필요가 없다.
                    break;
            }
        }
        System.out.println(result);
    }

    // 하나의 집합으로 만들기
    private static boolean union(int a, int b) {
        int aRoot = findParent(a);
        int bRoot = findParent(b);

        if(aRoot == bRoot) return false; // 이미 합쳐진 상태라는 것 의미

        parents[bRoot] = aRoot; // aRoot에 bRoot와 그 자식들 붙이기
        return true; // 두 노드가 합쳐졌다는 것 의미
    }

    // 최종적으로 찾은 부모 반환
    // 주의: 집합의 최상위 루트노드를 반환하지는 않음
    private static int findParent(int node) {
        if(node == parents[node]) return node;
        else return parents[node] = findParent(parents[node]);
    }

    // 자기자신을 부모노드로 세팅
    private static void makeSet() {
        parents = new int[N]; // 1번 노드부터 존재

        for(int i = 0; i < N; i++) {
            parents[i] = i;
        }
    }

    // Edge Object: weight 에 따라 오름차순
    private static class Edge implements Comparable<Edge> {
        int from, to, weight;

        Edge(int from, int to, int weight) {
            this.from = from;
            this.to = to;
            this.weight = weight;
        }

        @Override
        public int compareTo(Edge o) {
            return weight - o.weight;
        }
    }
}

2) 관련 문제 - 백준 1774 - 우주신과의 교감 (골드 3)

우선순위 큐를 이용하여 크루스칼을 구현하였습니다. 위 문제에서는 List를 이용한 Kruskal, 본 문제에서는 PQ를 이용한 kruskal 입니다

백준 1774 - 우주신과의 교감 링크

import java.util.*;
import java.io.*;

public class Main_1774 {

    static int N, M, parents[], points[][];
    static Queue<Edge> edgeList;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer stk = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(stk.nextToken());
        int M = Integer.parseInt(stk.nextToken());
        points = new int[N+1][2]; // 1번 노드부터 시작하기 때문에 N+1, 각 좌표 값을 가지고 있음
        edgeList = new PriorityQueue<>();

        parents = new int[N+1];

        // 자기자신으로 부모 노드 세팅하기
        for(int i = 1; i <= N; i++) {
            parents[i] = i;
        }

        // N개 노드의 좌표 값 담기
        for(int i = 1; i <= N; i++) {
            stk = new StringTokenizer(br.readLine());
            int x = Integer.parseInt(stk.nextToken());
            int y = Integer.parseInt(stk.nextToken());

            points[i][0] = x;
            points[i][1] = y;
        }

        // 이미 연결된 노드의 에지를 0으로 세팅하여 넣기
        for(int i = 0; i < M; i++) {
            stk = new StringTokenizer(br.readLine());
            int node1 = Integer.parseInt(stk.nextToken());
            int node2 = Integer.parseInt(stk.nextToken());

            edgeList.add(new Edge(node1, node2, 0));
        }

        // 모든 노드들이 서로 연결되었을 때의 거리 구하여 에지리스트에 넣기
        for(int i = 1; i < N; i++) {
            for(int j = i + 1; j <= N; j++) {
                double distance = getDistance(i, j);
                edgeList.add(new Edge(i, j, distance));
            }
        }

        // Kruskal Algorithm - 최소 비용 탐색
        double result = 0;
        int cnt = 0;

        while(!edgeList.isEmpty()){
            Edge edge = edgeList.poll();
            if(union(edge.node1, edge.node2)) {
                result += edge.distance;
                if(++cnt == N-1)
                    break;
            }
        }

        System.out.printf("%.2f", result);
    }

    private static double getDistance(int a, int b) {
        double squareX = Math.pow(points[a][0] - points[b][0], 2);
        double squareY = Math.pow(points[a][1] - points[b][1], 2);

        return Math.sqrt(squareX + squareY);
    }

    private static boolean union(int a, int b) {
        int aParent = findParent(a);
        int bParent = findParent(b);

        // 이미 한 집합에 속해있으면 추가해줄 필요가 없음
        if(aParent == bParent) return false;

        // 한 집합에 속한 경우가 아니라면, 속하게 만들어줄 것
        if(aParent < bParent)
            parents[bParent] = aParent;
        else
            parents[aParent] = bParent;
        return true;
    }

    private static int findParent(int node) {
        if(node == parents[node]) return node;
        else return parents[node] = findParent(parents[node]);
    }

    private static class Edge implements Comparable<Edge> {
        int node1; // 시작하는 노드
        int node2; // 연결된 노드
        double distance;

        public Edge(int node1, int node2, double distance) {
            this.node1 = node1;
            this.node2 = node2;
            this.distance = distance;
        }

        @Override
        public int compareTo(Edge e) {
            return distance < e.distance ? -1 : +1;
        }
    }
}