
✔ 미리보기
1. 행렬과 행렬의 연산
- 행렬
- 행렬의 합과 스칼라 곱
- 행렬의 곱2. 특수한 행렬
- 대각 행렬
- 항등 행렬과 영행렬
- 전치행렬
- 대칭행렬과 교대행렬
- 삼각행렬3. 행렬의 기본 연산과 사다리꼴
- 행렬의 기본 연산
- 행 사다리꼴 (Echelon Form)
- 계수 (Rank)
- 행렬의 표현과 응용
1. 행렬과 행렬의 연산
✔ 행렬
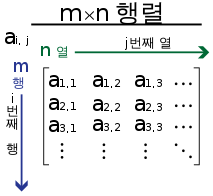
- 가로줄을 행(Row), 세로줄을 열(Column)이라고 부르며, m X n 행렬은 m개의 행과 n개의 열로 이루어진 행렬이다.
- 행벡터, 열벡터
- 행벡터 : [X1,...Xn] 1 X n 행렬
- 열벡터 : m X 1 행렬
✔ 행렬의 합과 스칼라 곱
- 행렬의 합과 차
- 두 행렬의 크기가 같아야만 연산 가능!
- 합 : A + B
- 차 : A - B (= A + (-B))
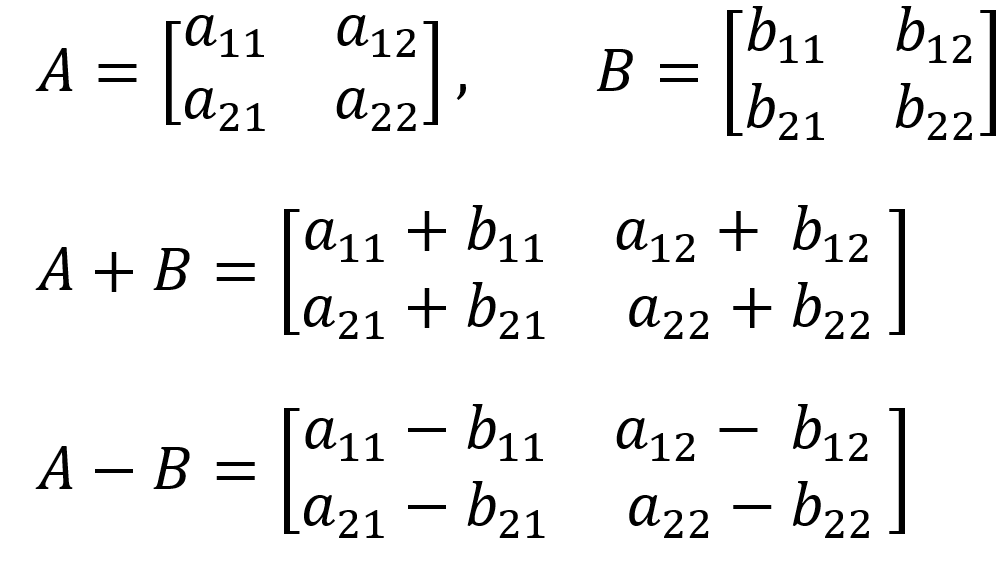
- 행렬의 스칼라 곱(Scalar Multiplication)
- 행렬 A에 실수 k를 곱하는 연산 => 행렬의 각 원소마다 k를 곱해준다.
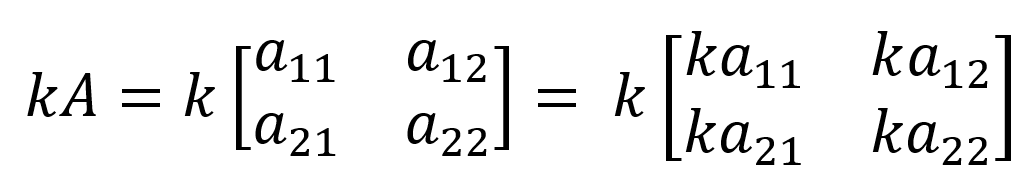
- 상등(equal)한 행렬
- 두개의 행렬에서 각각 대응하는 항들이 모두 동일하다면 상등하다고 한다.
✔ 행렬의 곱(Multiplication)
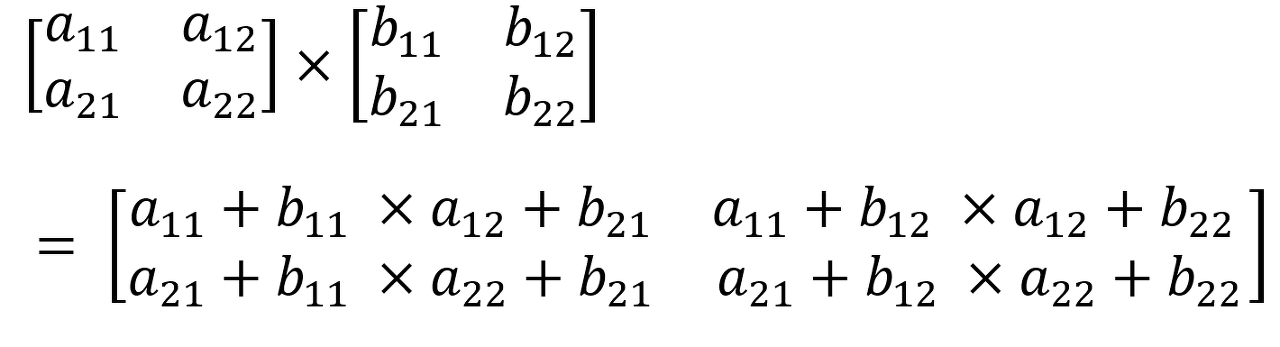
- (m X n) 행렬인 A와 (n X p) 행렬인 B 경우 AB = C 라 할때, C 는 (m X p) 행렬이 된다.
- A의 열의 숫자(n) B의 행의 숫자(n)가 같을 경우에만 정의 된다.
- AB 와 BA는 다른 값이다.(교환 법칙 성립 X)
- ex)
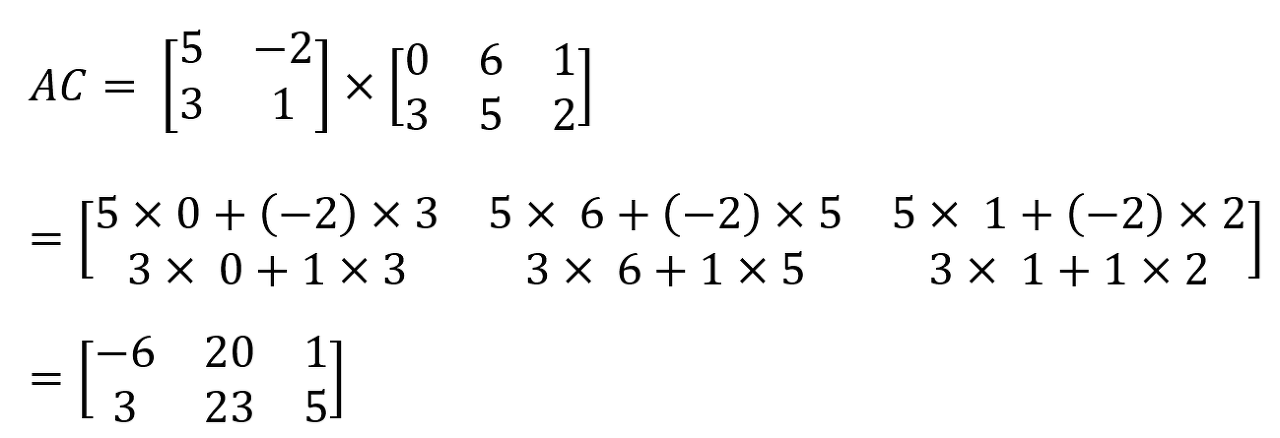
정리
- 곱셈의 결합 법칙 => A(BC) = (AB)C
- 배분 법칙 => A(B+C) = AB + AC
- 스칼라 곱 => k(AB) = (kA)B = A(kB)
- 행렬 곱셈의 항등식 => In = A = AI (I는 항등 행렬)
행렬의 거듭 제곱
- A가 nXn 행렬이고 k가 양의 정수라고 할때 A의 k승은 A를 k번 곱한느 것이다.
- A의 0승은 I(항등행렬)
부행렬 (submatrix)

2. 특수한 행렬
✔ (n차) 정방행렬 (Square matrix)
- n 개의 행과 n개의 열을 가지는 행렬
- 주대각선 :
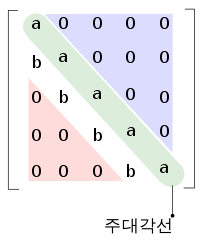
정방행렬에서의 다음과 같은 대각선을 주 대각선(Main diagonal) 이라 부른다. - 주 대각선 위의 모든 성분들을 대각항이라고 하고, 각 대각항의 합을 대각합(trace)라고 하며
tr(A) 또는 trace(A)로 표기한다.
대각합 특성
=> A와 B가 같은 크기의 정방행렬인 경우
✔ 대각 행렬 (Diagonal matrix)

- 주 대각선 성분이 아닌 모든 성분이 0인 정방 행렬이다.
✔ 항등 행렬 (Identity matrix)
- 대각행렬이면서 대각선의 항들이 모두 1인 정방행렬을 항등행렬 또는 단위행렬이라 한다.

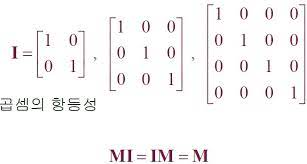
✔ 영행렬 (zero matrix)
- 성분이 모두 0인 행렬
- 기호로는 O로 적는다.
- A+O=O+A=A
✔ 전치행렬 (Tranpose matrix)


- 전치 행렬 성질

✔ 대칭행렬 (symmetric matrix)
- 정방행렬 n X n행렬이 자신의 전치 행렬과 똑같을때 대칭행렬이라 한다.
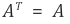
✔ 교대행렬 (symmetric matrix)
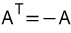
- 전치행렬에 음수를 곱한것과 같을 경우 교대행렬이라 한다.
✔ 삼각행렬 (Triangular matrix)
- 주대각선 위에 있는 모든 항들이 0인 행렬을 하부 삼각행렬
- 주대각선 아래에 있는 모든 항들이 0인 행렬을 상부 삼각행렬이라한다.
- 상부 삼각행렬의 전치는 하부 삼각행렬이고, 하부 삼각행렬의 전치는 상부 삼각행렬이다.
3. 행렬의 기본 연산과 사다리꼴
✔ 기본 행 연산(Elementary row operation)

- 행 동치 : 기본 행 연산을 필요에 다라 한번 또는 여러 번 거친 것
- 기본 행렬 : n X n 항등 행렬에서 한번의 기본 행 연산을 거쳐 만들어지는 행렬
- 피벗 : 행렬의 각 행에서 0이 아닌 가장 처음 나타나는 수를 행렬에서 피벗으로 삼을 수 있다.
✔ 행 사다리꼴(row echelon form)
m X n 행렬 A가 기본 행 연산들을 거친 후 다음 3가지 조건을 만족시키면 행 사다리꼴이라 한다.
- (1) 0으로만 이루어진 행들이 있는 경우, 행렬의 아래쪽에 나타낸다.
- (2) 모두가 0은 아닌 행의 가장 왼쪽에 가장 처음 나타나는 0이 아닌 수를 피벗으로 삼는다.
- (3) 모두가 0은 아닌 연이은 두 행이 있으면 아래쪽 행의 피벗은 위쪽행의 피벗보다 오른쪽에 있다
- 위 세개의 조건을 만족하면서 <각 행의 피벗을 포함하는 열에는 피벗 이외의 항들은 모두 0 이다 > 를 만족하면 "기약 행 사다리꼴"(reduced row echelon form) 라 한다.
✔ 기약 행 사다리꼴을 구하기 위한 기본 행 연산
- 전향단계(forward phase) : 피벗의 아랫부분이 0이 되도록 한다.
- 후향단계(backward phase) : 피벗의 윗부분까지 0이 되도록 한다.
- 전향 단계까지만 실행시 => 행 사다리꼴 (=가우스 소거법)
- 전향 단계 + 후향단계 실행시 (=가우스-조단 소거법)
- 계수(rank)
- 행 사다리꼴로 만들었을 때 <행 전체가 0이 아닌 행의 개수 = 피벗의 개수 = 계수>
