[알고리즘] DFS & BFS

BFS & DFS

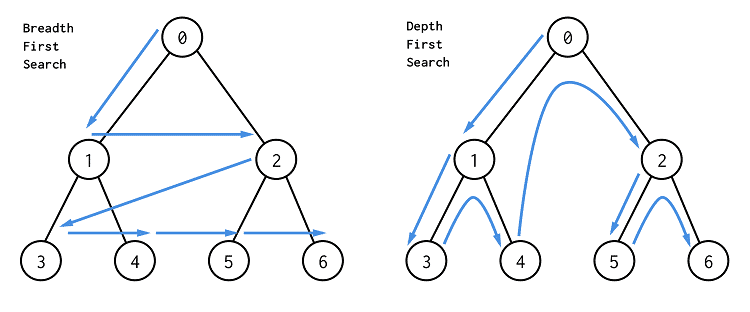
💞 깊이 우선 탐색(DFS)란?

< DFS : Dept First Search >

• 그래프 전체를 탐색하는 방법 중 하나로 시작점부터 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하고 넘어가는 방법
• 구현에는 스택을 통해 구현 / 재귀함수로 구현 2가지 존재
  => 재귀함수로 구현이 더 간편

DFS 코드

//인접 리스트를 이용한 dfs 구현

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

typedef struct incidenceType{
	int vertex;
	struct incidenceType *next;
}incidence;
typedef struct vertextType{
	incidence *head;
	int vertex;
	int isVisited;
}vertext;
typedef struct graphType{
	vertext *vertext;
}graph;

void makeEdge(graph g,int v1,int v2);
void DFS(graph g,int v);

int main(){
	int n,m,s,i,v1,v2;
	graph g;

	scanf("%d %d %d",&n,&m,&s); //정점개수, 간선 개수, 조사 시작할 정점 번호
	//그래프 초기화
	g.vertext = (vertext*)malloc((n+1)*sizeof(vertext));
	for(i=1;i<=n;i++){
		g.vertext[i].vertex=i;
		g.vertext[i].isVisited=0;
		g.vertext[i].head = (incidence*)malloc(sizeof(incidence));
		g.vertext[i].head->next = NULL;
		g.vertext[i].head->vertex =0;
	}

	for(i=0;i<m;i++){
		scanf("%d %d",&v1,&v2);
		makeEdge(g,v1,v2);
	}

	DFS(g,s);

	return;
}

void makeEdge(graph g,int v1,int v2){
	incidence *node1,*node2,*new1,*new2;
	node1 = g.vertext[v1].head;
	node2 = g.vertext[v2].head;

	new1 = (incidence*)malloc(sizeof(incidence));
	new2 = (incidence*)malloc(sizeof(incidence));

	new1->next = NULL;
	new1->vertex = v2;
	new2->next = NULL;
	new2->vertex = v1;
	// 정점 번호 순서대로 넣음
	while(node1->next!=NULL){
		if(node1->next->vertex>new1->vertex)
			break;
		node1 = node1->next;
	}
	new1->next = node1->next;
	node1->next = new1;

	while(node2->next!=NULL){
		if(node2->next->vertex>new2->vertex)
			break;
		node2 = node2->next;
	}
	new2->next = node2->next;
	node2->next = new2;
}

void DFS(graph g,int s){
	incidence *node = g.vertext[s].head;

	if(g.vertext[s].isVisited == 1)
		return;

	g.vertext[s].isVisited = 1;
	printf("%d\n",s);

	while(node->next!=NULL){
		DFS(g,node->next->vertex);
		node=node->next;
	}
}

DFS 시간복잡도

인접 리스트로 구현 : O(n + m)
인접 행렬로 구현 : O(n^2)

💞 너비 우선 탐색(BFS)란?

< BFS : Breadth First Search >

• 그래프 전체를 탐색하는 방법 중 하나로 시작점으로부터 인접한 노드를 먼저 탐색하는 방법
• 구현에는 큐를 통해 구현

BFS 코드

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

typedef struct incidenceType{
	int vertex;
	struct incidenceType *next;
}incidence;

typedef struct vertextType{
	incidence *head;
	int vertex;
	int isVisited;
}vertext;

typedef struct graphType{
	vertext *vertext;
}graph;

typedef struct nodeType{
	int data;
	struct nodeType *next;
}node;

typedef struct queueType{
	node* head;
}queue;

void makeEdge(graph g,int v1,int v2);
void BFS(queue *q,graph g,int v);
void enQueue(queue *q,int data);
int deQueue(queue *q);

int main(){
	int n,m,s,i,v1,v2;
	graph g;
    
	//큐 초기화
	queue *q = (queue*)malloc(sizeof(queue));
	q->head = (node*)malloc(sizeof(node));
	q->head->next = NULL;
	q->head->data = 0;

	scanf("%d %d %d",&n,&m,&s); //정점 개수, 간선 개수, 탐색시작할 정점 번호
    
	//그래프 초기화
	g.vertext = (vertext*)malloc((n+1)*sizeof(vertext));
	for(i=1;i<=n;i++){
		g.vertext[i].vertex=i;
		g.vertext[i].isVisited=0;
		g.vertext[i].head = (incidence*)malloc(sizeof(incidence));
		g.vertext[i].head->next = NULL;
		g.vertext[i].head->vertex =0;
	}

	for(i=0;i<m;i++){
		scanf("%d %d",&v1,&v2);
		makeEdge(g,v1,v2);
	}

	BFS(q,g,s);

	return;
}

void makeEdge(graph g,int v1,int v2){
	incidence *node1,*node2,*new1,*new2;
	node1 = g.vertext[v1].head;
	node2 = g.vertext[v2].head;

	new1 = (incidence*)malloc(sizeof(incidence));
	new2 = (incidence*)malloc(sizeof(incidence));

	new1->next = NULL;
	new1->vertex = v2;
	new2->next = NULL;
	new2->vertex = v1;
	
    // 정점 번호 순대로 삽입
	while(node1->next!=NULL){
		if(node1->next->vertex>new1->vertex)
			break;
		node1 = node1->next;
	}
	new1->next = node1->next;
	node1->next = new1;

	while(node2->next!=NULL){
		if(node2->next->vertex>new2->vertex)
			break;
		node2 = node2->next;
	}
	new2->next = node2->next;
	node2->next = new2;
}

void BFS(queue *q,graph g,int s){
	int v;
	incidence *node;
    //시작 정점 삽입
	enQueue(q,s);
	g.vertext[s].isVisited = 1;

	while(q->head->next!=NULL){
		v = deQueue(q);
		printf("%d\n",v);

		node = g.vertext[v].head;
        //인접 정점 큐에 삽입, 방문처리
		while(node->next!=NULL){
			if(g.vertext[node->next->vertex].isVisited==0){
				enQueue(q,node->next->vertex);
				g.vertext[node->next->vertex].isVisited = 1;
			}
			node = node->next;
		}
	}
}

void enQueue(queue *q,int data){
	node *newnode;
	node *tmp = q->head;

	newnode = (node*)malloc(sizeof(node));
	newnode->data = data;
	newnode->next = NULL;

	while(tmp->next!=NULL)
		tmp = tmp->next;
	tmp->next = newnode;
}
int deQueue(queue *q){
	int ret;
	node *del;
	node *tmp = q->head;

	del = tmp->next;
	tmp->next = del->next;
	ret = del->data;
	free(del);
	return ret;
}

BFS 시간복잡도

인접 리스트로 구현 : O(n + m)
인접 행렬로 구현 : O(n^2)

💞 DFS & BFS 응용

• 최단경로 : BFS
• 이중 연결 요소 : DFS
• 신장숲, 연결 요소, 경로, 싸이클 : DFS, BFS

신장 트리 , 신장 숲

• 신장 트리 (Spanning Tree) : 그래프의 정점들을 가지고 있는 트리(연결되고 , 싸이클이 없음)
  => n개의 정점을 n-1개의 간선으로 연결
  => 구현 : DFS or BFS 도중에 사용된 간선들만 남겨두면 된다.
  
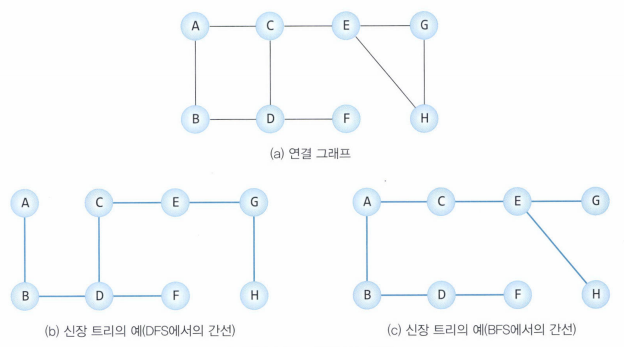
• 신장 숲 (Spanning forest) : 그래프가 연결되어 있지 않을 때 신장트리를 만들수 없다.
  => 각 연결된 요소들이 신장 트리들을 가짐