[알고리즘] 이론 시험 대비 끄적끄적

이정은·2021년 12월 8일

algorithm

필자의 학교 시험 대비로 정리하고자 한다.
개인적으로 아무렇게나 때려 쓰면서 정리할 예정이라
밑도 끝도 없이 요점만 있을 가능성이 높음,,,
의식의 흐름으로 정리,,,

* 알고리즘 시간 복잡도 순서

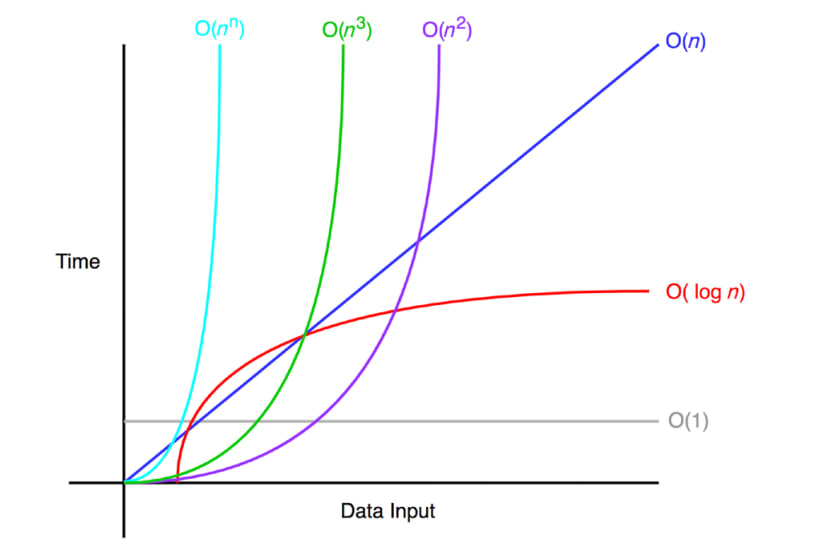
시간 복잡도 크기 순서
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!)

* 우선순위 큐와 큐

큐는 FIFO 구조로 먼저 들어간것이 먼저 나오는 구조
우선순위 큐는 들어간 순서와 관계없이 우선순위가 높은 데이터가 먼저 나온다
우선순위 큐로 무슨 자료구조가 가장 구현하기 적합한가? => 힙
( 배열이나 연결 리스트가 삭제에서는 시간 복잡도의 우위를 점할지라도, 삽입의 시간 복잡도가 힙 기반이 월등하기 때문에, 편차가 심한 배열과 연결리스트보다는 힙으로 구현)

* 정렬 알고리즘 정리

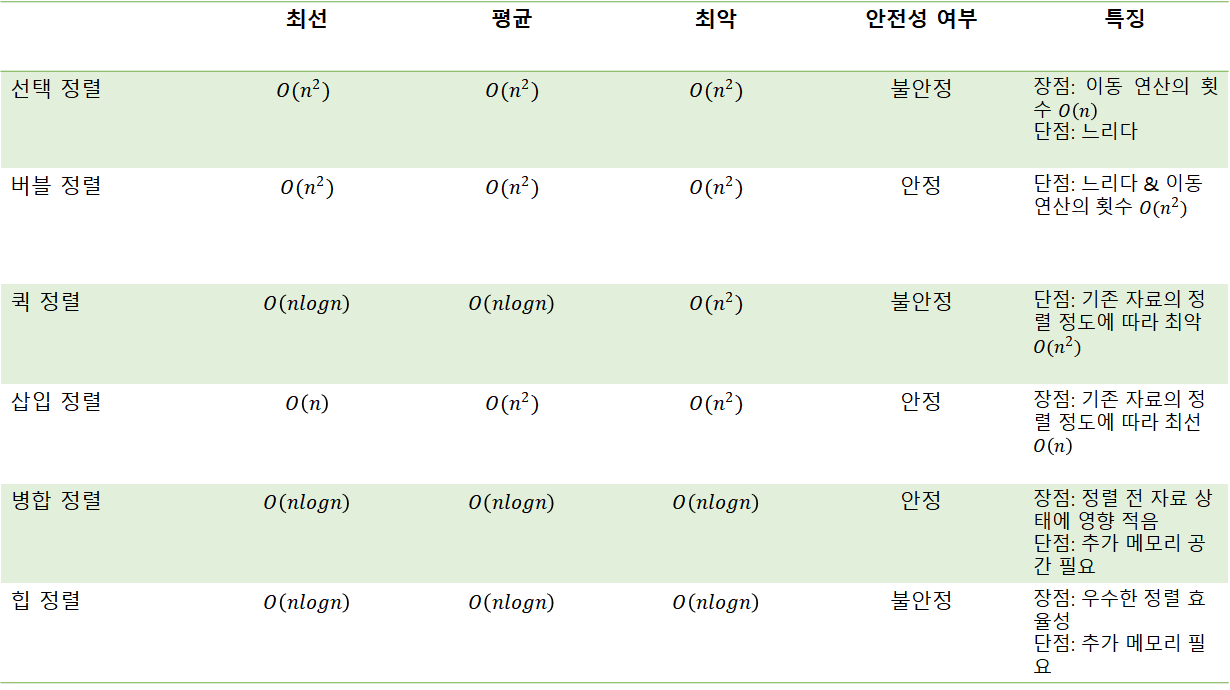
( 정렬의 자세한 코드는 제 velog 확인 )

합병 정렬, 삽입 정렬, 버블 정렬만 안정 정렬이다.
삽입 정렬 최선의 경우 O(n) -> 처음부터 자료가 정렬되어있는경우 => 자료가 정렬이 되어있을수록 빠르다
힙 정렬 -> 위의 표는 어디서 가져왔는데 힙정렬은 추가 메모리 없이 제자리 정렬도 가능하다.
(합병정렬만 추가 메모리 필요)
합병 정렬, 퀵 정렬 알고리즘 설계기법 => "분할 통치법" (분할->정복(재귀)->합병(통치))
합병 정렬 외부 메모리 필요, 순차적 데이터 접근
퀵 정렬 최악의 경우 O(n^2)
=> pivot(기준원소)가 항상 유일한 최소이거나 최대원소일 경우
=> LT 와 GT 중 하나는 크기가 n-1, 다른쪽은 크기가 0
우선순위 큐 (선택 : 무순리스트 , 삽입 : 순서리스트, 힙 : 힙)
분할 통치 (합병,퀵)

사전 ADT

분할 통치 vs 이진 탐색
분할 통치 : (정렬시) 이등분된 두개의 범위 모두 고려
이진 탐색 : (탐색시) 이등분된 두개의 범위 중 한쪽을 고려대상에서 배제

이진 탐색 트리
key(lchild) < key(parent) <= key(rchild)
완전 이진트리로 전제
탐색 성능 최악(O(n)) 최선 O(log n)

AVL Tree
높이 균형 속성 ( 트리의 모든 내부 노드에 대해 자식들의 좌우 높이 차이가 1을 넘지 않는다)
탐색,삽입,삭제 O(log n)

Splay Tree
트리의 노드가 탐색 또는 갱신을 위해 접근된 후, 스플레이되는 이진 탐색 트리를 말합니다.
(스플레이 된다 = 해당 노드가 루트로 이동된다)
탐색,삽입,삭제 O(log n) (상각실행시간)
AVL보다 구현이 더 간단

해시 테이블
버켓 배열 + 해시 함수
해시함수 => 무작위하게 분산 ,가능한 상수시간
임의의 키 => < 해시코드 맵 > => < 압축 맵 >
압축맵 ( 나누기 , 승합제( |ax + b| % M {a % M != 0}) )

충돌 해결
- 분리 연쇄 법 ( 테이블 외부에 추가적인 공간 요구)
- 개방 주소법 ( 공간절약, but 삭제가 어려움 , 군집화 발생 )

   - 선형 조사법 
    => 바로 다음 테이블 셀에 저장 (1차 군집화 발생)
    
   - 2차 조사법
    => 1 , 4, 9, 16 ...다음 테이블 셀에 저장(2차 군집화 발생)
    
   - 이중 해싱!!!
    => 군집화를 최소화
    더하는게 함수값임 함수값과 M은 서로소관계 
    cf) M은 소수이면 더 좋음 => 소수가 아니면 충돌 발생 가능성이 더 높음