.png)
여태까지 베이즈 정리를 그냥 조건부 확률이라고만 알고있었다. 단단히 잘못 알고있었다.
그래서 매번 시험에서 틀리는데 틀리는 이유조차 모르고 학기를 끝냈었다.
이번에 확실하게 알아보자!
✅ Bayes' Theorem
- 베이즈 정리의 의미와 의의
베이즈 정리는 단순히 조건부 확률을 풀어낸것이 아니다.
새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신 해 나가는 방법이다.
- 베이지안 주의?(Bayesianism)
또한 베이지안 주의 관점으로 확률을 보면 전통적인 확률관(빈도주의)와는 다르다.
베이지안 주의 관점으로 보면 확률은 "주장에 대한 신뢰도"라고 할수있다.
예를 들어 주사위를 던져 1이 나올 확률을 1/6하는 것을 빈도주의에서는 600번 던졌을때 100번은 1이 나올 것이다 해석하는 것이고, 베이지안 주의에서는 주사위가 1이 나왔다는 주장의 신뢰도가 1/6라고 보는 것이다.
- 용어
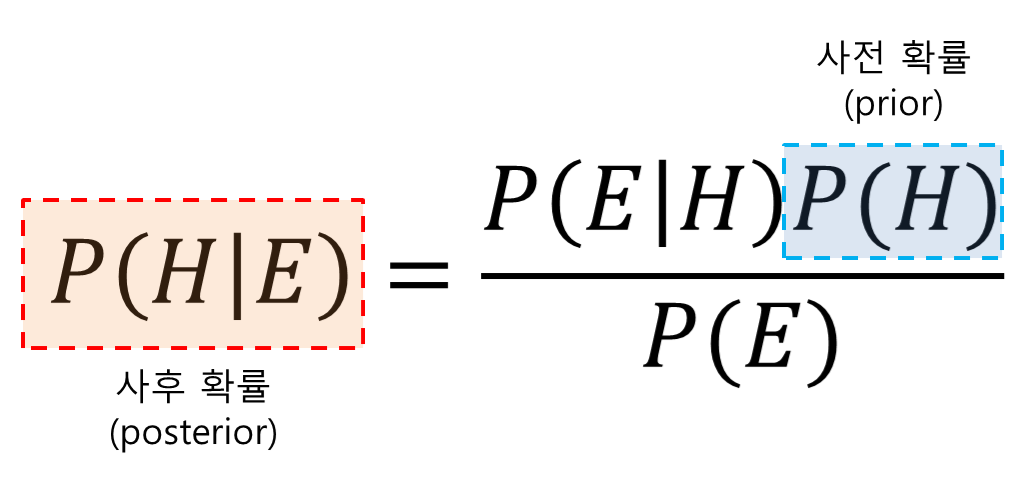
H : Hypothesis (가설) => 어떤 사건이 발생했다는 주장
E : Evidence (증거) => 새로운 정보
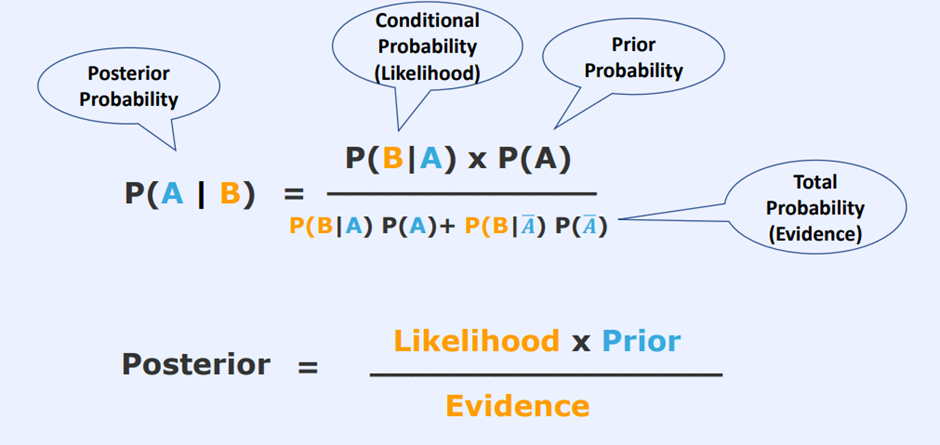
Posterior probability : 사후 확률
Likelihood : 우도 (가능성)
Prior probability : 사전 확률
Evidence : 증거
베이즈 정리는 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리다.
베이즈 확률론 해석에 따르면 베이즈 정리는 사전확률로부터 사후확률을 구할 수 있다.
먼저 단어부터 들이대 보았다. 근데 또 일단 문제부터 한번 풀어보자.
가장 흔한 예시 질병이다.
예제
질병 A의 발병률은 0.1%로 알려져있다. 이 질병이 실제로 있을 때 질병이 있다고 검진할 확률(민감도)은 99%, 질병이 없을 때 없다고 실제로 질병이 없다고 검진할 확률(특이도)는 98%라고 하자.
만약 어떤 사람이 질병에 걸렸다고 검진받았을 때, 이 사람이 정말로 질병에 걸렸을 확률은?
📜 solution
-> 먼저 hypothesis와 Evidence를 정의해보자
evidence : 새로운 정보 => 질병에 걸렸다고 검진을 받았을때 (positive)
hypothesis : 주장 => 정말로 질병에 걸렸다
=> 구하고자 하는 것 : P(H|E)
그러므로
질병 A의 발병률은 0.1%이므로
임의의 사람이 이 질병에 걸렸을 확률은 P(H)로 쓸 수 있으며, P(H)=0.001 이다.
민감도:
특이도 :
위의 식

와 같이 조건부 확률만 알아도 풀 수 가있다.
하지만 베이즈 정리의 진정한 의의는 알기 어렵다.
베이즈 정리의 진정한 의의는
사전확률을 모르는 상황에서 사전확률을 가정하고,
발생한 사건(새로운 정보)를 토대로 사전확률을 "갱신" 해나가는데 있다.
다음 예시를 보자.
예제
상대가 나를 좋아하는지 궁금한 상황이다. 그런데 상대방이 먼저 나에게 디엠이 왔다고 하자.
여기서 사전확률은 그가 나를 좋아할 확률이다. 그가 나를 좋아할 확률? 잘모르겠다.
좋아하지도 싫어하지도 않는것 같다. 그러면 좋아할 확률을 0.5라고 사전확률을 놓자.
이제 상대방의 행동을 기반으로 사전확률을 갱신해나갈 것이다.
상대방의 행동 => 나에게 디엠을 보낸 것이다
이제 알아야 할 것은
상대방이 나를 좋아하는데 먼저 디엠을 보낼 확률 : P(D|L)
상대방이 나를 좋아하지않는데 먼저 디엠을 보낼 확률 : P(D|L')
이 확률을 안다는 것이 비현실적이긴 하지만 여러명을 조사해본결과
P(D|L) = 0.6
P(D|L') = 0.4 이라고 하자
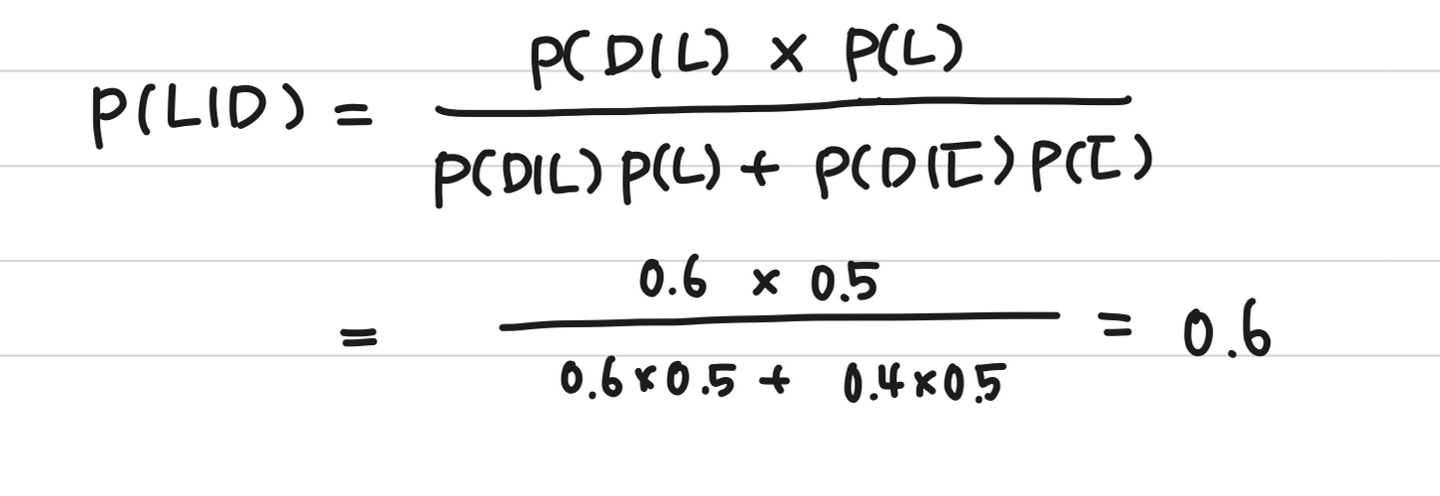
그렇다면 다음과 같이 구할수있다.
그러면 디엠을 받음으로써 상대방이 날 좋아 할 확률이 0.6로 갱신되었다.
이것을 베이즈 갱신이라 하며 갱신된 확률을 사후 확률이라고 한다.
이 상황에서 상대방이 영화를 보자고 한다면? 다시 새로운 정보가 들어온 것이다
그러면 앞에 구한 사후확률은 다음 갱신에서 사전확률이 된다.
이제 갱신된 상대방이 나를 좋아할 확률은 0.6이다.
이제 상대방의 행동을 기반으로 사전확률을 갱신해나갈 것이다.
상대방의 행동 => 나에게 영화를 보자고 하였다.
이제 알아야 할 것은
상대방이 나를 좋아하는데 먼저 디엠을 보낼 확률 : P(M|L)
상대방이 나를 좋아하지않는데 먼저 디엠을 보낼 확률 : P(M|L')
또 이 확률을 조사해본 결과
P(M|L) = 0.7
P(M|L') = 0.3 이라고 하자
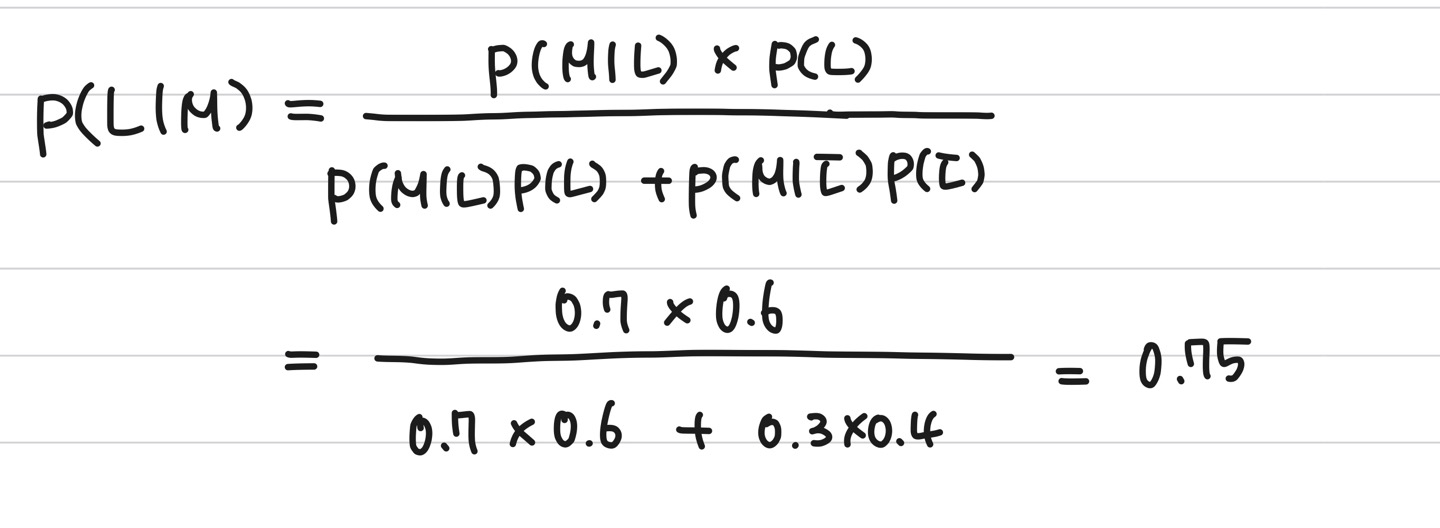
그러면 다음과 같이 또 0.75로 갱신된 것을 볼 수있다.
베이즈 정리는 이와 같이 갱신해 나가는 것에 의의가 있다.
