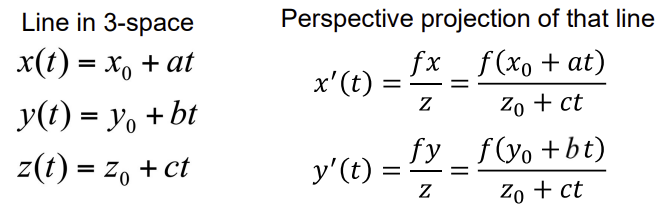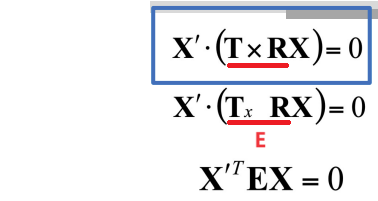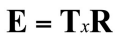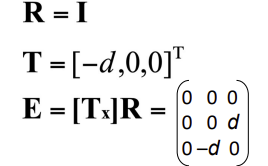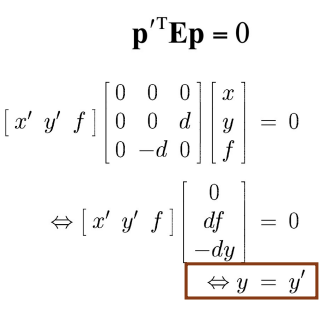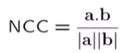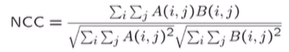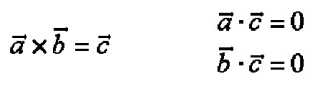[컴퓨터 비젼] CV-08 Stereo Vision

1.
Background
- 한 이미지 = 3D 공간을 projection한 결과
-> projection할 때 depth로 크기만 결정하고 없앰
-> 이미지에서 depth를 알아낼 수 있을까?
사람의 depth perception
- 두 눈, 두 귀 -> 공간감/입체감 -> 두 개의 다른 정보를 합성하여 이해하기
stereo vision
- 카메라 두 대를 사용해서 depth를 알아내기
- 시야각이 다른 두 이미지를 조합하여 depth 찾기

- 한 이미지로만 depth를 알지 못하는 이유
: 3D 공간에서 다른 두 점이, pp에 같은 점으로 projection되는 경우, depth를 알 수 없음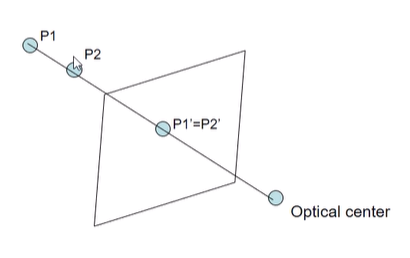
Monocular cues to depth
- 사람이 한 눈으로 봤을 때 파악하는 깊이는 두 종류
- Absolute depth cues
- Relative depth cues
사람의 Relative depth perception (Monocular)
- Occlusion
- 사람은 두 개 이상의 물체가 어떤 관계(ex Occlusion
무엇을 가리는가; 장면의 구조)를 보고 depth를 알아낼 수 있다
- Texture
- 동일한 texture가 반복되는 경우, texture의 변화(크기, 방향)로 depth를 알아낼 수 있다
- ex) 일정한 밀도를 가진 딸기씨 -> 딸기씨의 밀도로 reconstructure (딸기씨 밀도가 낮아지면 가깝다)
- Shading
- 조명의 방향에 따라 밝기 변화
- 빛에 따른 기울기(변화도)를 파악하고 적분하면 깊이
-> shapeformshading
- Shadows
- Inter-refections (서로 반사)
- Perspective effects
- Atmospheric
- 멀리 있는 것은 공기층에 의한 빛의 산란 현상으로 뿌옇게, 흐리게, 밝게 보임
- horizon line
- 수평선에 가까운 것은 머니까 작게보임
- moon illusion (수평선과 상관없이 달의 크기는 동일함; 수평선과 가까운 달은 멀 것이다 -> 커보임, 수평선과 먼 달은 가까울 것이다 -> 작아보임)
사람의 Absolute depth perception (Monocular)
Conflicting
- Perspective vs Familar size
- 벽선, 물체의 크기 등으로 평평한 perspective가 느껴지는 상태에서 familar size가 어색하게 느껴지는 상황이 존재하곤 함(상충됨)

- Scene vs Objects
- 배경 인식: 사과가 크게 느껴짐

- 물체 인식: 배경이 작게 느껴짐

- Texture surface layout -> wrong recognition of absolute scale

others
- (not mococular) 물체의 Motion을 찍은 여러장의 이미지로 depth를 알아낼 수 있다 (shape from motion)
- (not human, in camera) 고정된 카메라에서 focus를 바꿔가며 찍은 것들의 선명해진 곳을 파악해 depth 알아냄 -> depth from focus
Stereopsis: Multi-view in human
- not monocular
- Stereopsis: 두 눈으로 입체적인(depth) 지각을 하는 과정
- fovea: 디테일한 정보를 알 수 있는 시야
- 사람은 초점을 맞추기 위해 회전하고, 이 때의 수정체 텐션을 기억하여 얼마나 멀리 있는지 추측할 수 있다
- 물체에 따라 visual angle이 다르다-> Disparity
Stereo: Multi-view in camera
- 상관관계를 알고있는 두 개 이상의 static한 카메라 (또는 motion을 알고있는 한 카메라로의 dynamic 촬영)를 사용해 depth 측정
-> shape from motion between two views: Stereo
- "shape from X:
- X: shading, texture, focus, Motion...
- shading, texture, focus 등은 조건과 미리 알고있어야하는 정보가 많음
-> Motion으로 해보자!
Stereo
- 다른 시각을 가지는 이미지들로부터 3d shape 추정
- 두 pp에서 같은 물체로의 ray가 만나는 점이 실제 3차원에서의 위치
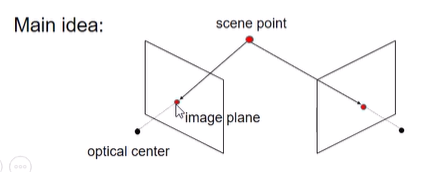
- consider:
- 카메라 위치, 상관 관계 (calibration)
- 각 이미지의 동일한 점 (matching)
camera calibration: The process of computing the camera parameters
Camera parameters in Stereo
- extrinsic: 두 카메라의 R, T 차이점
- interinsic은 같다고 가정

Geometry for a simple stereo system
- 카메라 2대가 x축으로 translation 차이만 존재하는 상황에서 Depth
z 구하기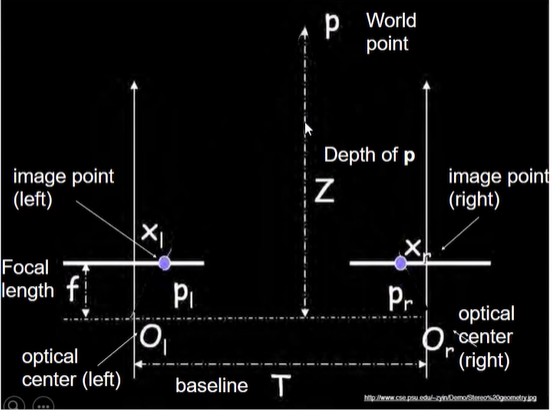
- 두 삼각형의 닮음비 사용
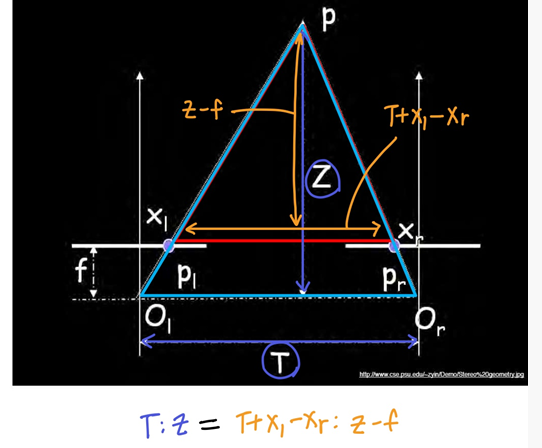
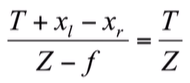
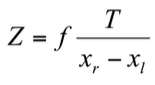
- 이때, xr−xl = Disparity (카메라를 이동했을 때, 한 피사체가 이미지에서 움직인 양)
- depth
Z는 T, f, disparity에 영향을 받는데, T와 f는 카메라 세팅에 따라 정해진 값이므로 disparity가 중요하다
- Disparity가 커지면, 분모 커짐, Z 작아짐
-> 카메라를 이동했을 때, 한 피사체가 이미지에서 많이 이동했다면 가까운 물체이다
Disparity
- 카메라가 움직일 때, 멀리있는 것과 가까운 것의 이미지 상에서의 움직임 속도 차이가 존재함을 알 수 있다
- ex) 차에서 건물들은 빨리 움직이고 산은 천천히 움직임
- 가까운 것은 disparity가 크고
1, 먼 것은 disparity가 작다0 -> 두 이미지에서 corresponding point를 찾았다면 Disparity로 상대적인 깊이를 알 수 있다⭐
-> 두 이미지에서 corresponding point를 찾았다면 Disparity로 상대적인 깊이를 알 수 있다⭐
Stiching에서 Disparity와 translation의 관계
- 거리가 다른 두 물체가 한 이미지에 같이 있는 경우
- 카메라가 이동하여 translation이 발생하면 disparity가 0보다 커지고, 두 물체의 이미지상의 속도가 달라 가려지는 부분이 발생할 수 있다 -> 대응점 찾기 어렵다
- translation하지 않고 rotation만 적용했다면 T=0, disparity=0이므로 대응점을 찾기 수월하다
(12/8 녹강 4분대.. 이해 잘 안댐)
Stereo matching algorithm: window-based matching
- 두 stereo 이미지는 x축으로만 translation됐다는 성질 이용

- 한 이미지의 점
x에서 window 설정
- 그 window를 다른 이미지의 scanline을 따라 이동시키며 best match
x'을 찾는다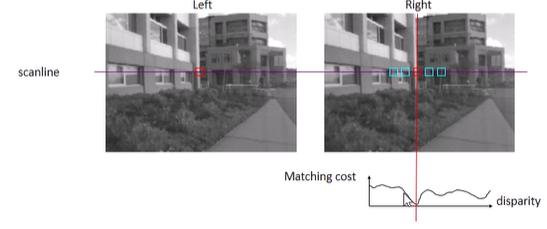
- SSD나 normalized correlation을 사용해 best match를 찾음
- 하지만 두 이미지의 밝기를 유지시키기 어려운 photometric 차이가 있으므로 correlation을 사용하기도 함
x-x'으로 disparity 계산- Depth 계산
- 위와 같은 계산은 이전 corresponding point를 찾던 2차원 방법을 1차원으로 풀 수 있게 해줌
window size and desparity map
- window 크기가 작으면
- 작은 window와 비슷하게 생긴 부분이 많아 noise가 생길 수 있음
- more detail, more noise
- window 크기 크면
- 특정 점의 depth만 찾고 싶은데 주변 픽셀의 영향이 커서 디테일이 부족해짐
- less detail, smoother disparity map, rough
- optical flow의 window 문제와 비슷하게, window 안에 다른 depth를 가진 픽셀이 존재하여 best match를 찾기 위해 계산할 때 그 중간의 depth를 찾게되며 smooth 효과
- 아래 사진에서 나무가 앞에 있는 건 알지만 나무 모양은 알기 어려움

Failures of correspondencs search
- Texture less surface
- 텍스쳐가 없는 배경

- Occlusions
- 한 씬에 가까이 있는 물체와 멀리 있는 물체가 겹쳐있는 경우
- 거리가 달라 이미지 상의 속도가 다른 두 물체의 겹쳐짐 때문에 보이는 모습이 달라지면 일치하는 점이 존재하지 않을 수도 있다
- 창들과 사람 겹치는 부분

- Repetition
- 같은 부분이 반복되는 경우

- Non-Lambertian surface
- 바라보는 방향에 따라 highlight(specular)가 이동하는 경우
-> bright constancy X
Problem of window-based matching
- 두 카메라를 평행하게 맞추는 것과, 밝기, focal length등을 동일하게 맞추기 어려움
- 정확한 depth
z를 찾으려면 disparity가 큰 것이 좋다 (오차 줄이기)
- disparity = fT/Z로 식을 변형하였을 때, f와 T에 비례
- f는 고정이므로, T가 커지는 것이 좋다
-> 하지만, 카메라 이동이 많이되면 같은 피사체가 이미지에 보이지 않는 경우가 생길 수 있음 (가까울수록 심함)
- sol: 카메라 회전까지 추가하여 가운데로 모이도록...
2.
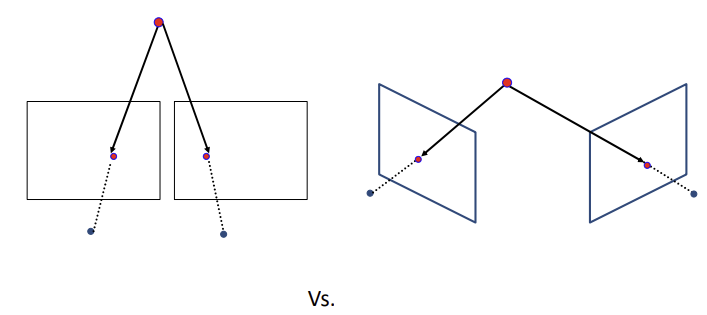
Pinhole camera geometry
- 삼차원 공간에서의 점
x0, y0, z0이 t만큼 이동했을 때 직선x(t), y(t), z(t)을 화면에 perspective projection해서 나타난 화면 상의 직선 x'(t), y'(t)
(f는 scale)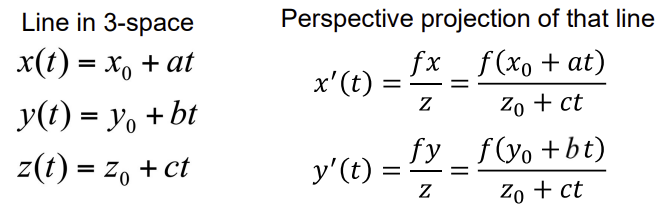
- 삼차원 공간에서 parallel하면 projection한 image plane에서도 parallel 하다.
- ex) 벽돌 정면 사진의 line ->
z0, y0이 변하지 않아 y'(t)도 변화 없음 -> 사진 상에서도 parallel
- homogrnrous coord에서 extrinsic과 intrinsic 합치기
- world coord에 extrinsic matrix 곱해서 camera coord로 변환
- camera coord에 intrinsic matrix 곱해서 pixel coord로 변환
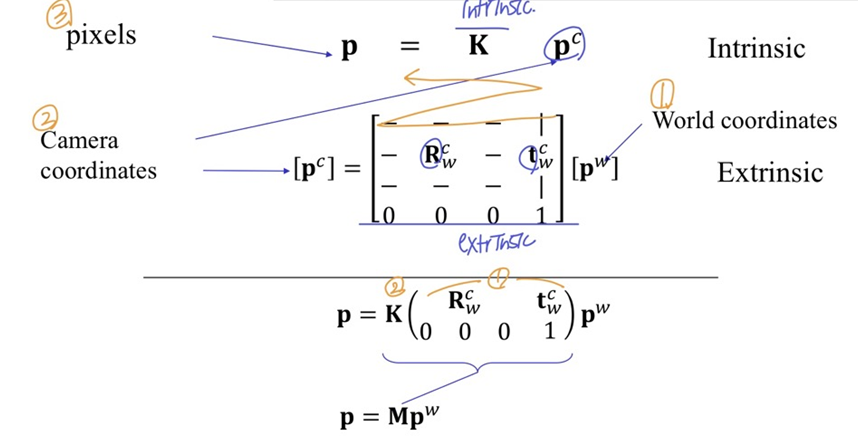
- p=Mpw는 아래와 같이도 표현할 수 있음
- M의 row vector
- 행렬의 곱을 dot product로 표현
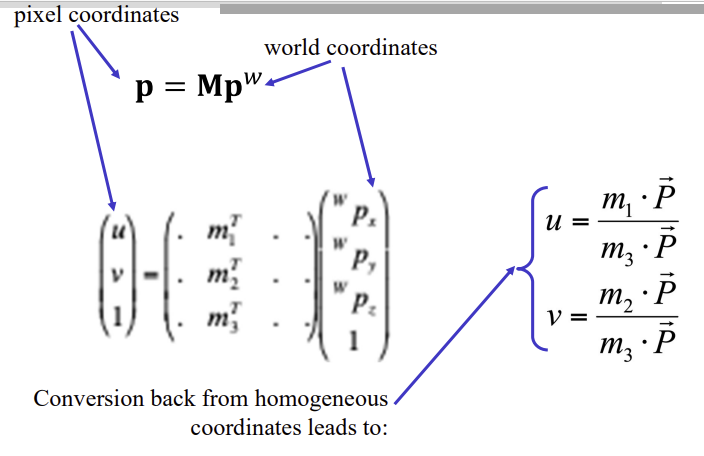
Calibrated camera: Stereo correspondence constraints
- 위에서 했던 것처럼 x축으로 translation만 한 경우에는 corresponding point를 찾기 쉬움
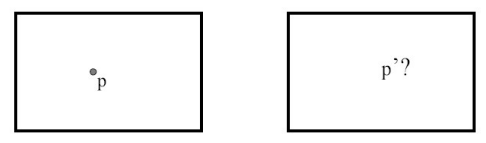
- 하지만 rotation까지 추가된 경우, 간단하지 않음(calibrated camera)
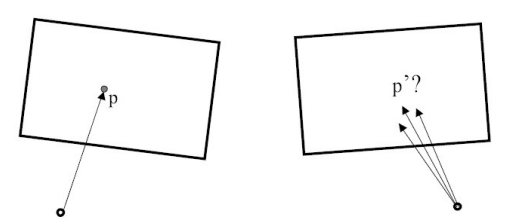
- 이동 전 점
p의 ray상에 존재할 실제 피사체
- 이동 후 점
p'은 그 피사체를 지나는 ray와 pp가 만나는 점
-> 실제 피사체 위치가 확실하지 않으므로, 그 피사체를 지나는 ray를 여러개 그릴 수 있고, 그 ray와 pp의 교선epipolar line으로 나타난다
-> 이동 후 점p'은 교선 위에 존재한다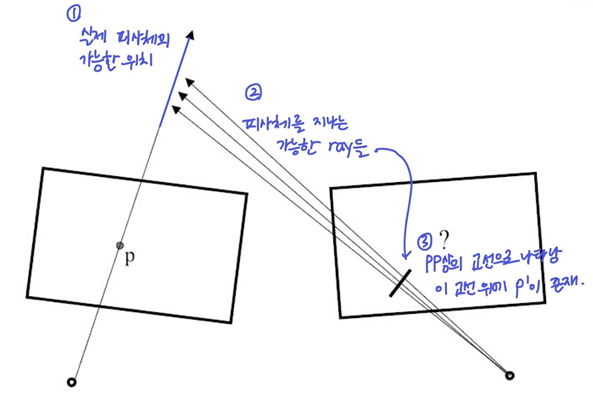
-> 이것이 epipolar geometry
Epipolar geometry
- 조건: corresponding pixel은 이동 전과 이동 후 이미지 둘 다에 항상 등장 (사라지지 않는다)
- 위의 과정을 반대로도 생각하면, 각 pp에 epipolar line이 그려지고, 그 때의 평면이 epipolar plane이다
- epipolar plane은 ray를 포함하고 세 픽셀을 지나는 평면
- epipolar plane과 pp와의 교선이 eplipolar line
- depth와 상관없이, 한 카메라의 epipolar line에 존재하는 점이면 그 점은 다른 카메라의 eplipolar line에 존재
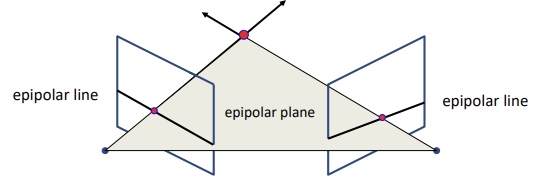
- 두 카메라의 CoP를 연결하여 Baseline 생성
- Baseline과 pp가 만나는 점 Epipoles 지정
- Baseline과 epipoles는 물체의 위치나 픽셀 상관 없이 정해지는 값 (카메라만 정해지면 구할 수 있음)
- world coord의 피사체 위치
P를 지정한다면 Epipolar plane 생성 가능 (Baseline과 P 연결)
- Epipolar plane과 pp의 교선 Epipolar Lines 지정
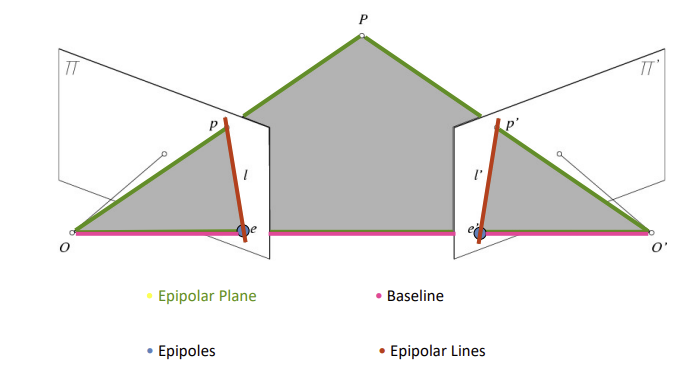
- 모든 epipolar line은 epipole을 지난다
- epipolar plane은 두 epipolar lines을 지난다
Epipolar constraint
- 한 이미지에서의 점
p의 실제 위치P를 지정한다면, epipolar plane을 사용하여 elipolar line 중 한 점p'을 지정할 수 있다
- 점
p의 corresponding point는 항상 l'에 존재
- 점
p'의 corresponding point는 항상 l에 존재
-> 대응관계
- 한 epiporlar line에 존재하는 점들의 대응점은 다른 epiporlar line에 존재
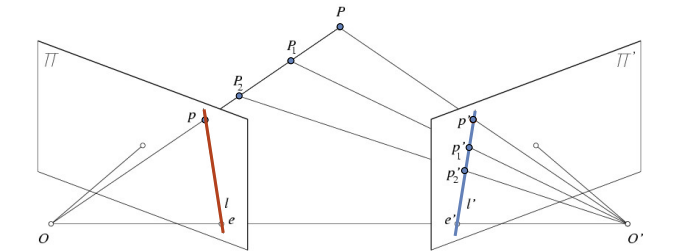
- 이전에는 corresponding point를 찾기 위해 이미지 전체를 확인하는 3차원 문제였는데, 이제는 disparity를 활용해 부분적으로 찾을 수 있는 1차원(line에서 한 점 찾기)문제가 됨
-> 한 점의 potential match(대응될만한 점)이 line에만 존재하니까 search space가 줄어듦
example
- Converging camera: 같은 물체를 다른 각도에서 본 경우(RT변화)
- 각 점의 epipolar line은 baseline을 중심으로 회전 (모든 epipolar line은 epipole을 지나니까)
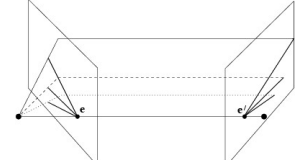

- motion parallel: x축 translation만 한 경우, 평행한 epipolar line이 나옴
- 다른 점을 기준으로 살펴봐도 계속 평행
Geometry -> Algebra
- 기하학적으로 epipolar를 이해했으니, 식으로 나타내보자 (epipolar line만)
- 카메라의 RT를 알고 있을 때, camera1 coord의 점에 RT를 적용하면 camera2 coord의 점이 나온다
X: world pointX의 camera1 coord (초록 벡터) (image plane 생각하지마)X': world pointX의 camera2 coord (노랑 벡터)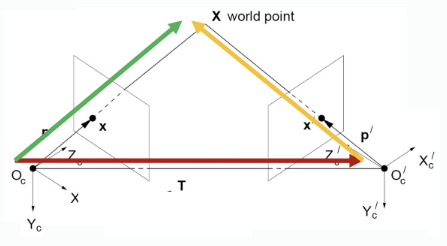
matrix로 나타낸 cross product
- a, b 외적의 결과는 a, b 평면에 수직인 벡터 c
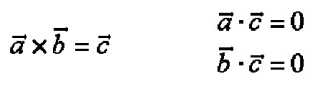
- b와 곱했을 때 c와 같은 결과를 나타내주는 a로 이루어진 행렬을 사용해 cross product를 나타냄
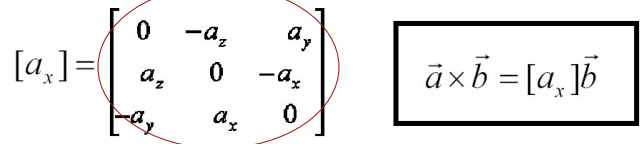
X는 camera1 coord의 점 x를 나타내는 벡터, X'은 camera2 coord의 점 x'을 나타내는 벡터- 벡터
X에 RT를 적용해 벡터X'으로 만듦
- 양변에 T를 외적하면
TxX'으로 epipolar plane과 수직인 벡터를 구할 수 있고, (TxT는 공통 수직이 없으므로 0)
- 그 벡터와
x'은 수직이므로 양변에 x'을 내적한 결과는 0이 나와야함 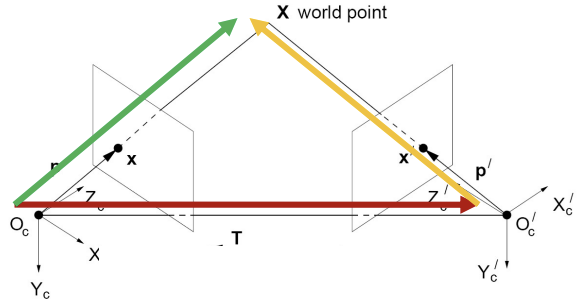
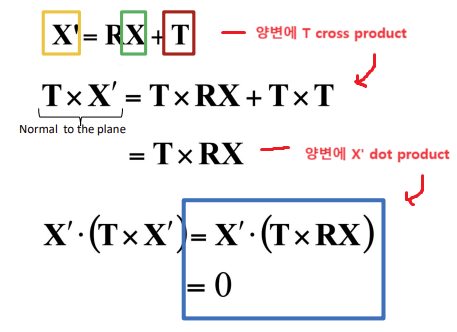
- 위 식의 우변 cross product를 matrix로 변형하고 (알고있는 T를 행렬로 바꿈) 그 부분을 E로 나타냄
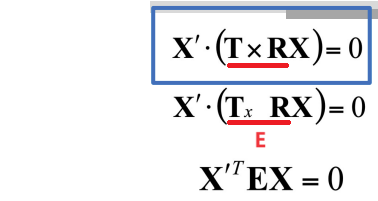
- image plane의 점 x와 x'를 나타내는 homogeneous coord(ray)를
p와 p'이라고 하면
- 위의 식을 적용시킬 수 있다
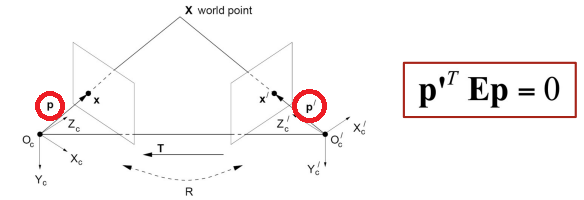
-> 카메라 뿐만 아니라 homogeneous coord(Ray)에도 적용되는 식
위 식을 역으로 하여 RT를 알아내는 과정이 stereo camera calibration
Essential matrix
- 위 식에서 E를 essential matrix
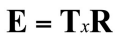
- 두 카메라의 RT의 관계를 나타내는 행렬 -> Extrinsic
(Intrinsic parameters는 알고있다고 가정하고 essential matrix를 사용)
- 이미지의 점과도 관련있는 행렬이다!
- essential matrix를 구하는 것이 camera calibration
- 알고있는 RT로 E를 구하거나
- 고정된 카메라에서 움직여가며 최적화된 E를 구할 수 있음
Essential matrix and epipolar line
- 한 이미지의 점의 homogeneous coord
p와 다른 이미지의 점의 homogeneous coord p'는 아래 식을 만족
- 위의 식으로 epipole line의 조건식을 만들 수 있다
- 점 p'가 정해졌을 때, p'의 대응점이 존재하는 line은 위의 식을 만족하는 p들의 집합 (ETp′와 수직인)
- 점 p가 정해졌을 때, p의 대응점이 존재하는 line은 위의 식을 만족하는 p'들의 집합 Ep와 수직인)
- 아래는 기하학적 설명...인데 어려웅
- cross product 형태로 보면 line이 나온다 (두 점을 외적하면 두 점을 지나는 직선)
- Ep : 점
p를 포함하는 epipolar line을 나타내는 coordinate vector
- ETp′ : 점
p'을 포함하는 epipolar line을 나타내는 coordinate vecotr
(강노에 적힌건데 먼말)
- Essential matrix로 epipolar line을 무한히 만들 수 있다
- 벡터
p와 ETp′를 내적하면 0이므로, ETp′는 p와 수직
-> 벡터 p는 여러개이고, 이 모든 벡터들과 공통적으로 수직인 ETp′는 epipole plane을 나타내는 normal
- ETp′: 오른쪽 camera coord에서 본 epipole plane의 normal
- p: ETp′와 수직인 벡터들의 집합 ->
p'에 대한 epipole line 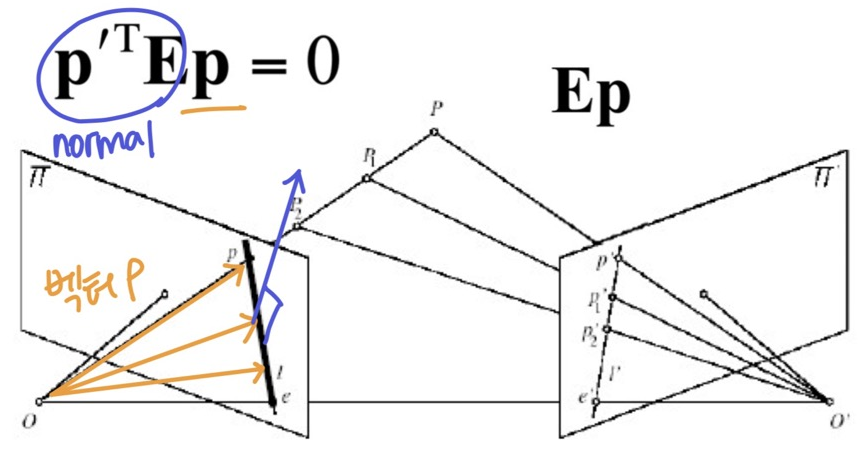
-> 점 p'가 정해졌을 때, p'의 대응점이 존재하는 line은 위의 식을 만족하는 p들의 집합
- (반대)벡터
p'을 기준으로 하면 Ep는 왼쪽 camera coord에서 본 epipole plane의 normal
example: parllel camera
- x축으로 translation만된 카메라
- rotation 없으므로
R=I
- x방향으로 -d만큼 움직였으므로
T=[-d, 0, 0]^T
- E는 아래와 같이 나타난다
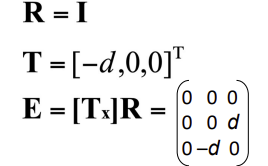
- E를 사용해서 epipolar line 계산
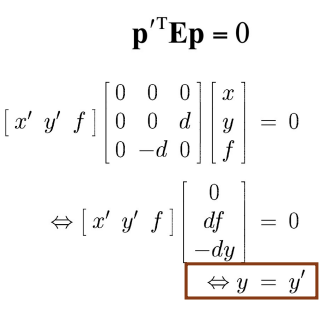
- epipolar line의 조건: y=y'(y값이 같은 line)
- y값이 같은 line이 epipolar line이므로, corresponding point는 같은 horizontoal line에 존재함을 알 수 있다
-> image scanline = epipolar line
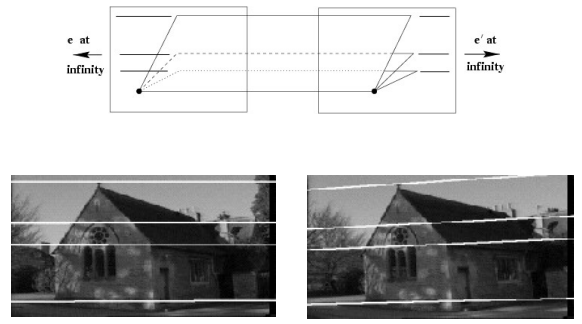
Stereo image rectification
- 위의 예시처럼, 두 이미지가 평행하면 계산이 간편
- parallel하지 않은 두 이미지가 평행할 수 있도록 가상 pp로 reprojection하여 x축으로 평행이동 한 것처럼 만든다
-> Epipolar line이 수평이 되며, 대응점 찾을 때 같은 높이의 scanline에서 찾으면 된다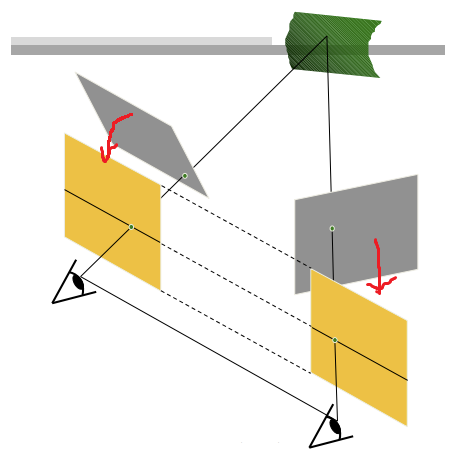
- perspective transform (homography)으로 rectification

Matching
- 두 epipolar line에서 대응점을 찾는 방법
- Window based method -> SSD, NCC
point to point
- Scan-line Stereo
scanline to scanline
- matches를 찾기 위한 조건:
- scene point가 두 이미지에서 보여야 함
- Similarity: matches 영역이 비슷하게 보여야 함
Intensity profiles
- 대응점을 찾기 위해 점을 찾는 것이 아닌, 라인을 찾는 문제!
- 두 epipolar line의 관계를 보면 밝기 양상이 똑같다.
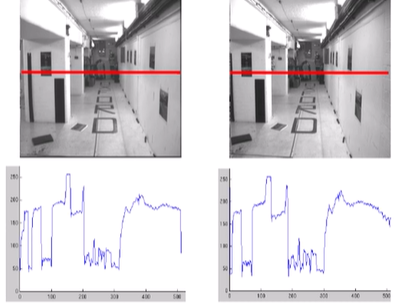
- textureless 부분도 찾을 수 있다
- 하지만, 밝기를 사용하므로 노이즈에 예민
- sol: window based(NCC), scan-line stereo
Dense vs Sparse Correspondence search
- Dense(전체): 한 대응점을 찾기 위해 라인 탐색
- scanline 전부 탐색하여 매칭

- Sparse(일부): 한 대응점을 찾기 위해 한 점 탐색
- feature로 동일점 찾기

1. Window based: NCC(Normalized cross correlation)
- window를 사용해서 대응점을 찾는 방법은 SSD와 NCC
- stereo에서는 보통 두 카메라를 사용하고, 동일한 노출값을 주기 어려우므로 photometric한 차이가 있어 NCC를 주로 사용
- a와 b의 내적을 normalize
- 범위가 [-1, 1]이 된다
- 이미지의 전체 밝기 상관 없이, 밝아지는 방향/정도를 파악하여 대응점을 찾기 위해 정규화한 것
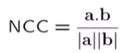
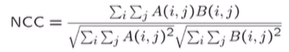
- 각 region의 픽셀값을 벡터 형태로 만듦 (아래 그림은 12차원의 벡터)
- 벡터 길이: 밝기 정도
- 벡터 방향: 밝기 방향, 모양 (밝은 쪽을 향함)
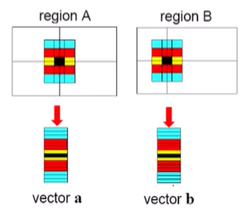
- 정규화를 하면 벡터 길이는 같아지므로 전체 밝기는 신경쓰지 않을 수 있고, 정규화된 벡터의 방향만 비슷하면 대응점
- 벡터 방향의 비슷한지 확인하기 위해 내적
-> 비슷하면 1, 다르면 작은 값
Problem of window based correspondence
- Textureless한 부분에서 대응점 찾기 어려움
- window 크기의 영향을 많이 받음 (위에 적힌 것)
- sol: 조건을 추가해서 scanline stereo 사용
2. Scan-line Stereo
Correspondence constraints
- scanline stereo를 사용해 대응점을 찾기 위한 epipolar geometry의 constraints
- Uniqueness
- 한 점에 대한 대응점은 1개(one pixel to one pixel)
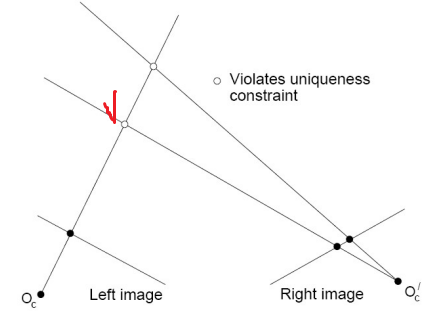
- Ordering
- 연속적으로 생긴(같은) 물체의 대응점의 순서는 바뀌지 않는다
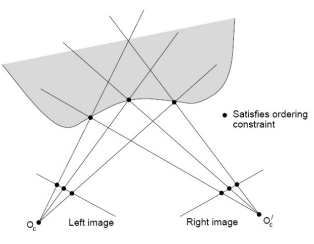
- 바뀌는 경우도 있긴하지만~ 고려하지 않음
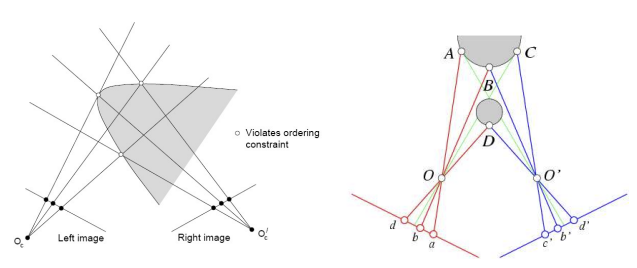
- Disparity gradient
- disparity가 급격하게 변하지 않을 것이다
- 한 점의 대응점을 선택할 때, disparity가 작은 점 선택
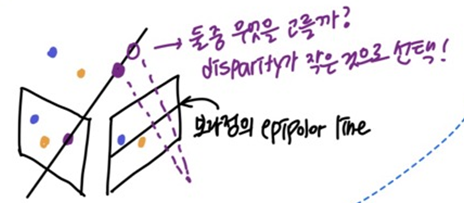
- 각 픽셀에 대해 independent(loca)하게 수행하던 window 방법과 다르게, 위의 조건(non-local constraint)이 들어가 픽셀들의 dependent한 성질(coherence)를 고려하여 매칭
- dynamic programming으로 scan-line stereo의 shortest-paths를 구한다
Shortest path with Dynamic programming
- Occlusion으로 가려진 것을 고려하며 매칭
- 세로는 왼쪽 이미지의 픽셀 나열, 가로는 우측 이미지의 픽셀 나열
- 각 셀은 매칭되는 픽셀이 얼마나 유사한지를 나타냄 (밝기 차이 + 올 수 있는 세가지 방향의 픽셀과의 차이 중 최소값)
- Correspondence:
- 알맞게 찾아진 매칭 -> 그래프에서 대각선으로 이동
- Right Occlusion:
- 오른쪽 이미지에는 있는데, 왼쪽 이미지에는 가려져서 안보이는 픽셀
- 오른쪽 이미지의 다음 픽셀과 연결을 시도 -> 그래프에서 오른쪽으로 이동
(left 변화x, right 변화o)
- Left Occlusion:
- 왼쪽 이미지에는 있는데, 오른쪽 이미지에서는 가려져서 안보이는 픽셀
- 왼쪽 이미지의 다음 픽셀과 연결을 시도 -> 그래프에서 왼쪽으로 이동
(right 변화x, left 변화o) (음의 disparity)
- 오른쪽, 왼쪽으로 이동한 거리는 disparity
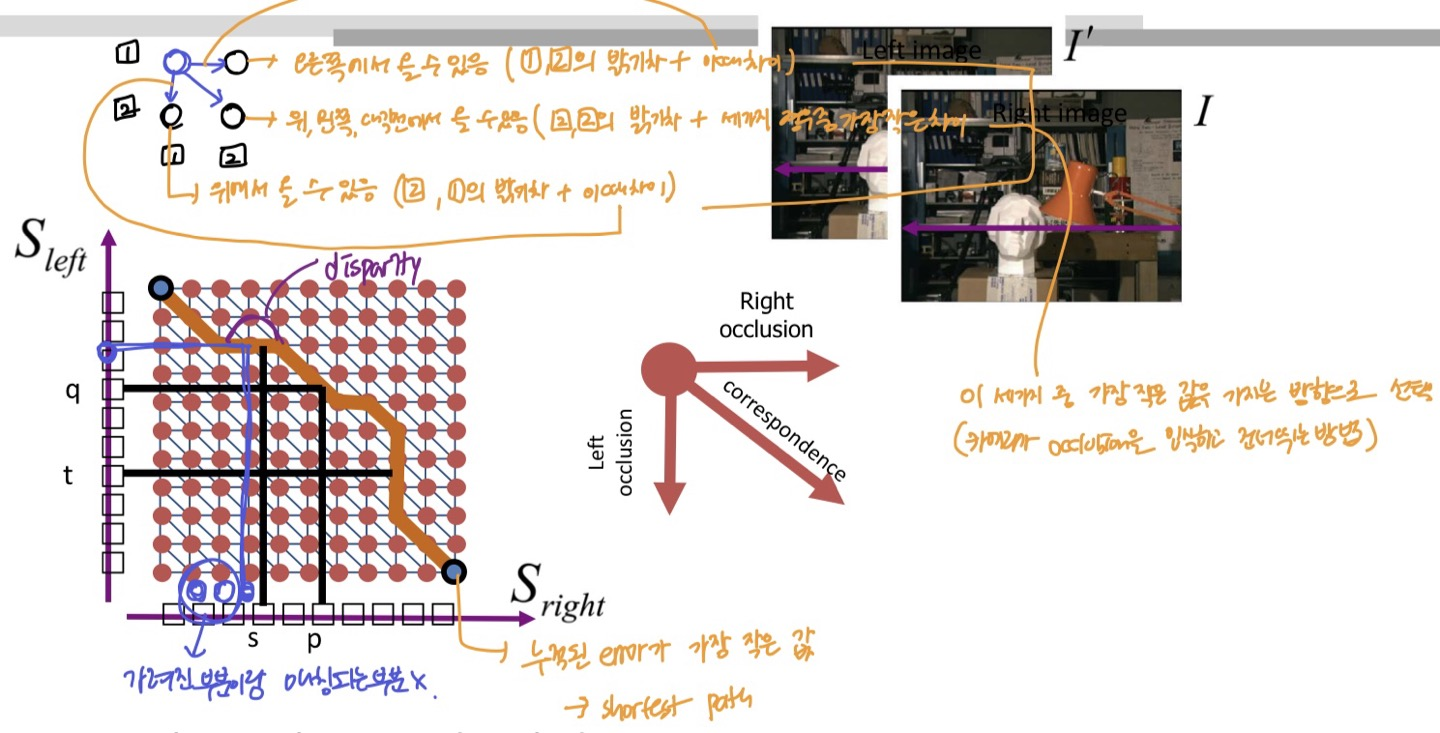
- 3가지 방향 중 밝기 차이가 가장 작은 값으로 이동하여 컴퓨터가 occlusion을 고려해 매칭하는 것
- 그렇게 찾은 path는 누적된 error가 가장 작은 path, error가 최소가 되는 매칭 -> shortest path
- 그리고, disparity를 알면 depth를 구할 수 있는 것이다~
- 위에서 추가한 조건때문에 3가지 방향으로만 갈 수 있음 (위, 왼쪽으로는 못감!)
Streaking artifacts problem
- scanline stereo는 scanline(가로선)만 보고 구하므로
- 결과에 가로선 형태
streaking과 scanline 주변으로 퍼져보이는 결과가 나타남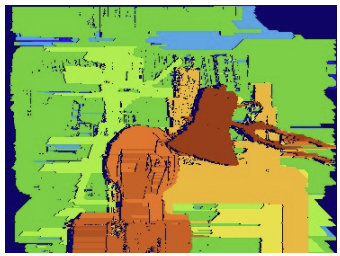
as enery minimize
- 대응점을 찾기 위한 E를 설정하고 (작을수록 좋은 energy) E를 최소화하는 문제로 해결
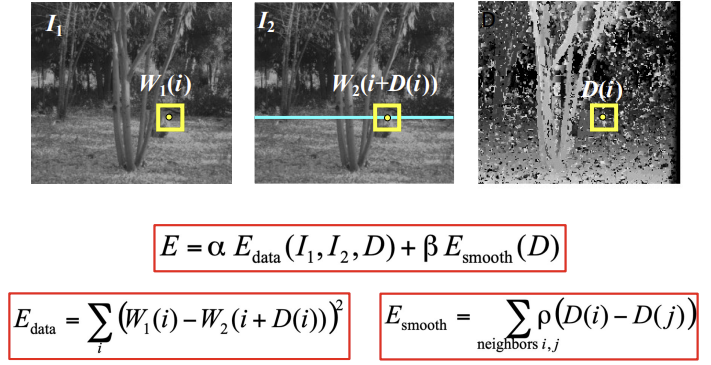
- 첫째 항은 disparity만큼 움직였을 때의 차이로 대응점을 잘 찾았는지를 나타냄
- 차이가 안나야지 같은 점이므로 최소가 되도록 해야함
- 두번째 항은 결과가 부드럽게 나왔는지 확인하는 것
- 자신 주변 disparity와 차이가 크면 noise가 있다는 것이므로 최소가 되도록 해야함
- noise 없이 잘 움직였다면 주변 움직임 양상도 비슷하여 disparity도 비슷할 것이다
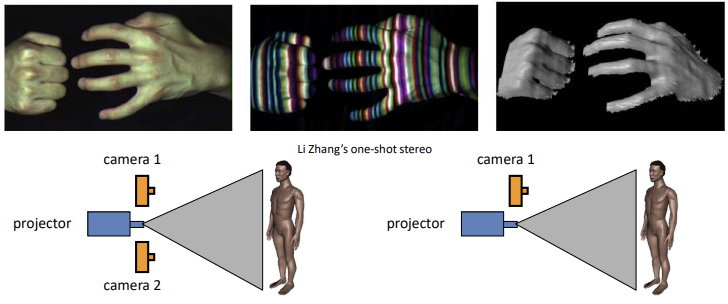
Active stero with structed light
- textureless한 부분의 대응관계를 찾기 위해 프로젝터로 structed light를 쏴서 texture가 나타나도록 함
- dynamic programming에서는 textureless한 부분은 그냥 linear하게 만들었고, 이 오류로 인해 망가질 수 있음









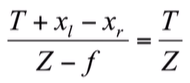
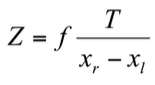
 -> 두 이미지에서 corresponding point를 찾았다면 Disparity로 상대적인 깊이를 알 수 있다⭐
-> 두 이미지에서 corresponding point를 찾았다면 Disparity로 상대적인 깊이를 알 수 있다⭐