- 0차원 점(corner)
- 1치원 선(edge)
- 2차원 면(regions)
Segmentation
- 비슷한 픽셀 그룹 만들기
Perceptual organization
- 사람은 작은 시각 정보들을 모아서 큰 단위로 합치는 과정(Grouping)으로 물체를 인식하고 상호관계를 파악
- grouping하는 방법은 여러가지 (gestalt priciple)
1. clustering
- grouping pixels
- 특정 점을 어느 그룹에 붙일까
- token: 픽셀들에 대한 성질들 (색, 밝기, gradient, texture measures 등..)
- Agglomerative clustering
- token이 비슷한 것끼리 묶어서 가까운 클러스터에 붙이는 것을 반복
- Divisive clustering
- 전체 이미지에서 다른 영역인 것 같으면 쪼개는 과정을 반복
- 배경이라고 생각되는 픽셀과 아닌 픽셀을 구분하여 영역을 찾아감
- Dendrograms
- Agglomerative(아래->위)와 Divisive(위->아래)는 반대 관계
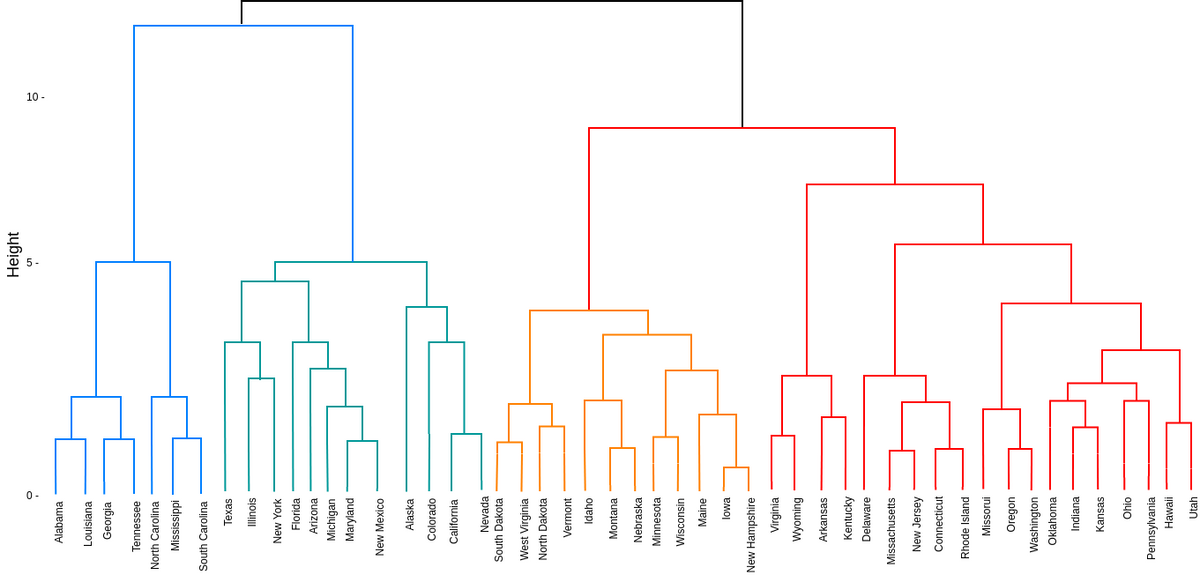
- ex
- Agglomerative: 1, 2의 거리가 가장 짧음 -> 1, 2의 중점과 가장 가까운 것은 3 -> ...
- divisive: 456, 123의 거리 가장 멂 -> 12와 3 거리 멂 -> ...
- Agglomerative(아래->위)와 Divisive(위->아래)는 반대 관계
이미지에서 같은 영역인지 아닌지 판별하는 방법은?
segmentation algorithm
- 각 픽셀마다 token벡터
z계산
- 두 픽셀/그룹끼리 얼마나 가까운지 measure하기 위해 clustering algorithm 사용 (k-means, mean shift)

1-1. K-means Clustering
- k개의 영역으로 쪼개기
- 랜덤하게 k개의 cluster center 선정
c1, ..., ck(k를 미리 정해야 됨) - 각 픽셀
p을 자신과 가장 가까운 centerci에 붙여 픽셀 그룹 만듦- 근데 랜덤하게 고른 센터라, 만약 영역의 가장자리가 센터로 지정되었다면, 같은 영역이 아닌 픽셀들이 더 가깝게 계산될 수 있음
- 그래서, 그룹의 평균을 내서 평균을 center 재지정
- 바뀐 center로 2, 3번 반복 (center와 그룹이 바뀌지 않을 때까지)
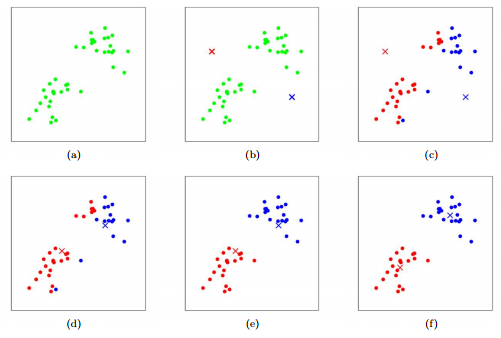
- 어쨋든 평균을 내서 구한 것이기 때문에 local minimum하긴 하지만, 영역의 정확한 center를 구하진 못하므로 glabal minimum은 아님
- 1번 과정의 랜덤하게 찍은 센터로 결과가 달라지므로.. 반복해서 그나마 좋은 결과를 찾는다 (np complete)
-> [각 클러스터의 center와 클러스터 내 픽셀들의 차이]를 모든 클러스터에서 계산했을 때 최소가 되도록하는 점 찾기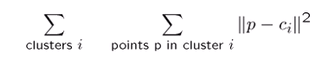
- 밝기의 평균으로 계산한 k-means
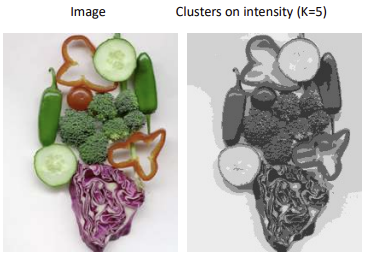
- 컬러의 평균으로 계산한 k-means
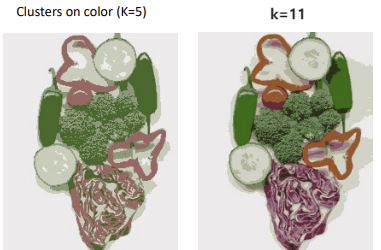
- 토마토와 양상추가 같은 덩어리로 뭉침 -> 같은 색이어도 거리가 멀면 다른 덩어리로 보자 (또한, 다른 색이어도 가까우면 묶을 수도 있음)
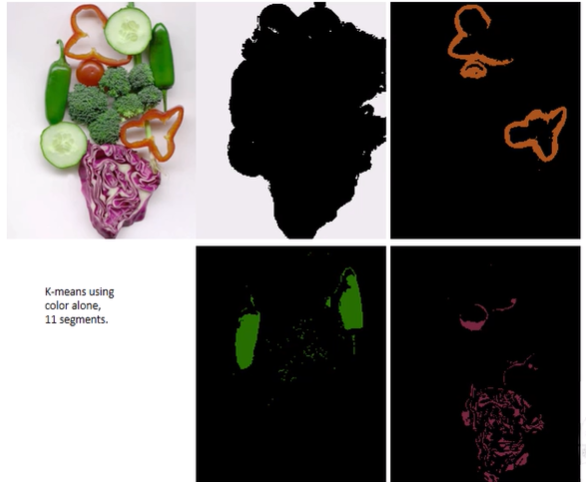
-> token에 x, y 추가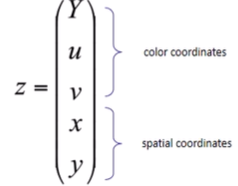
- 밝기의 평균으로 계산한 k-means
- problem: Image에 무엇이 있는지 알 수 없는 상태에서
k를 정하기 어려움
1-2. Mean Shift Segmentation
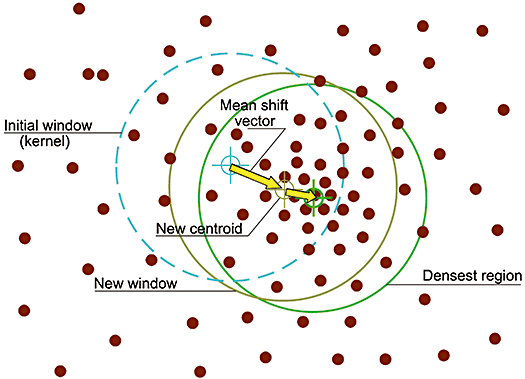
Mean shift
- search window 사이즈 설정 및 랜덤하게 초기 위치 설정
- search window안에서 평균 계산
- 그 평균으로 center를 가지는 window가 converge할 때까지 2번 반복
-> 밀도가 높은 곳을 찾아냄
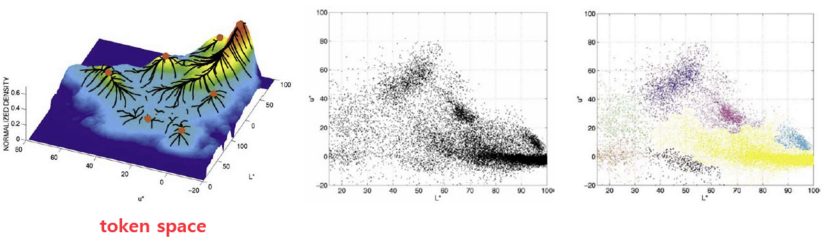
- 무조건 픽셀 위치에 따라 존재하는 spatial이 아닌, token space에서 진행 (color space .. 등등)
- image를 token으로 변경 (token space)
- 초기 search window 위치를 랜덤하게 설정 (k가 아닌 여러개 많이해서 골고루 퍼지도록)
- window안에서의 token 평균으로 center를 옮김 (mean shift window location 계산)
- window가 특정 위치로 converge할 때까지 3번 반복
- 여러 window가 같은 곳으로 converge되기도 함 -> 전부 같은 그룹
- window가 지나온 곳들은 같은 그룹
window size
- window 크기가 클수록 더 많이 묶음
2. Cutting
- connecting similar pixels
- 같은 그룹이 아닐 것 같은 픽셀 자르기
2-1. Graph-Theoretic Image Segmentation
- 각 픽셀들이 옆 픽셀과 관계를 가질 것이다.
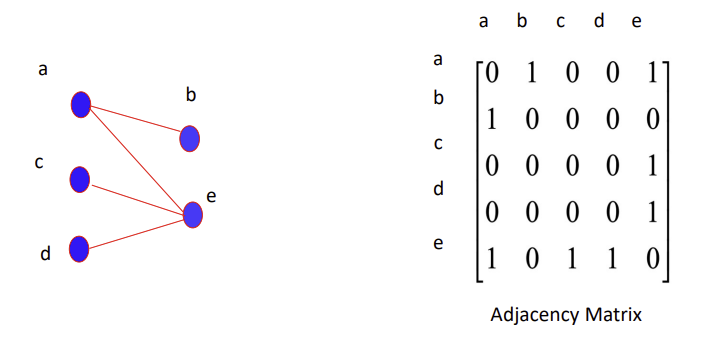
- 이때, 픽셀은 node(vertex)
V, 근처 픽셀과의 관계는 weighted edgeE로 설정하여 graphG=(V, E)생성
- weight를 가지는 edge는 두 픽셀이 같은 영역에 들어갈 확률
W을 나타냄 - Segmentation = graph partition (두 개의 독립된 형태로 쪼갬)
Graph Representations
- Adjacency Matrix로 픽셀 graph 나타냄
- 두 픽셀이 같은 영역에 들어갈 확률을 나타낸 Affinity Matrix로 weighted graph 나타냄
(undirected graph는 symmetric하다)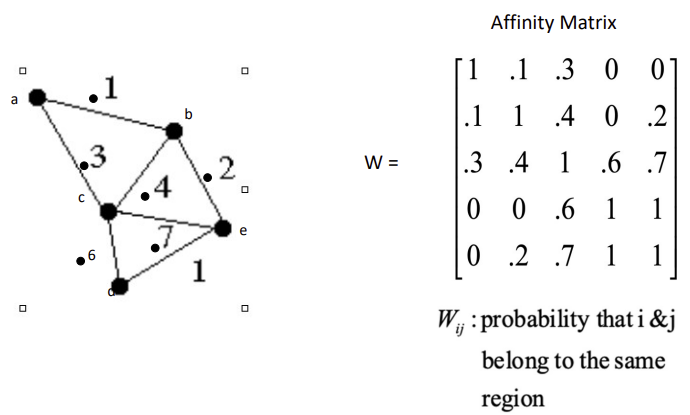
Weight (Affinity between pixel)
- Affinity: 두 픽셀이 얼마나 비슷한가, 근접한가
- 비슷한 픽셀끼리의 edge는 strong, 그렇지 않으면 weak
- 가우시안 형태로 pixel descriptor의 similarities를 확인
- token
z의 차(distance)가 작을수록 같은 영역일 확률이 큼 - 같은 영역: 거리가 0이므로 W는 1에 가까움
- 다른 영역: 거리차가 커질수록 W는 0에 가까워짐
- 가우시안을 사용하면 range[0, 1]가 정해진다는 장점
- 어디까지를 같은 영역이라 판단할지에 대한 변수는 σ
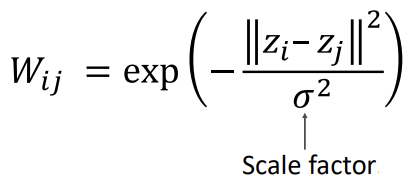
- token
- 하지만, 두 픽셀 사이에 Interleaving edge(두 픽셀 관계를 끊어주는 엣지)가 존재한다면 graph의 edge는 약해질 것 -> 아래 식으로 weight를 구한다
- Pb: 두 픽셀 사이에 edge가 존재할 확률
-> 두 픽셀 사이 gradient 크기를 사용해 구한다 (gradient가 크면 수직으로 edge가 존재할 확률이 크다)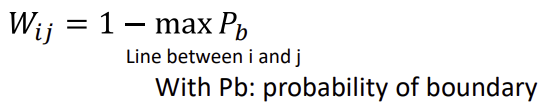
- Pb: 두 픽셀 사이에 edge가 존재할 확률
✔️ edge의 strength를 구하는 방법은 1개가 아니다...
Eigen vector
- eigen vector로 같은 영역인지 확인하기
- token(feature) space의 점들간의 관계 weight(affinity)를 계산
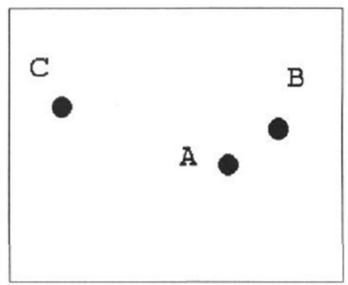

- 점들간의 관계W의 eigenvector를 계산하면 관계성이 보이고, A와 B가 같은 그룹임을 알 수 있음
- eigen values에 대한 eigen vector를 나타낸 것으로, 마이너스는 신경쓰지 않음
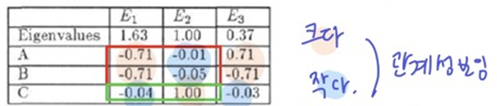
- eigen values에 대한 eigen vector를 나타낸 것으로, 마이너스는 신경쓰지 않음
- ex) 아래 points그림의 점들간의 관계를 adjacency matrix로 나타내고, 그 matrix로 eigen vector 계산
- 큰 값을 가지는 eigen vector들의 점을 찾아보니 같은 그룹이다
- 아래 좌측 하단 이미지는 위의 weight matrix (가로 A, B, C... 세로 A, B, C...로 구성되며 각 점들간의 관게를 나타낸 그림)
- scale factor
σ이 작을 수록 다 멀다고 판단하고(다 작은 값), 클수록 다 같은 그룹이라고 판단(다 큰값)
-> 큰지 작은지 판별할 수 있는 적당한 값을 찾아야 함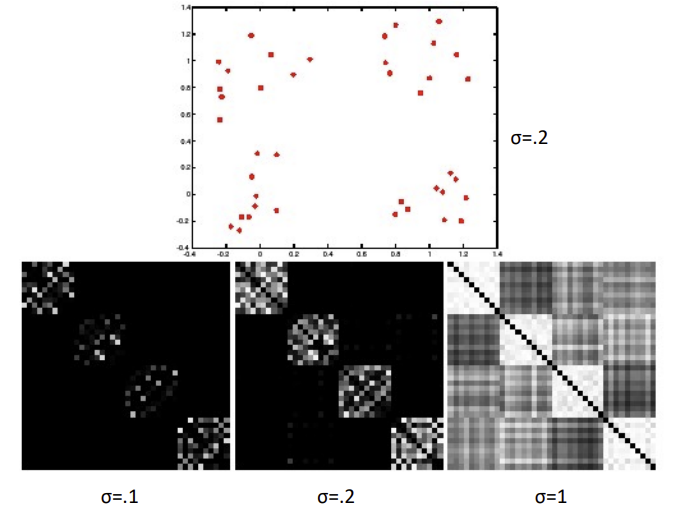
Boundaries of region
- 이미지 영역의 구분 기준은?
- 밝기/색: 힌계 존재
- 텍스쳐: 밝기가 달라도 같은 패턴이 나타나면 같은 영역
- Motion: 비디오의 경우 같은 방향으로 움직이면 같은 영역 (optical flow)
- Stereoscopic depth: 카메라 기준으로 depth가 비슷하면 같은 영역
- Familiar configuration: 사람에게 익숙한 것 (ex 얼굴)
용어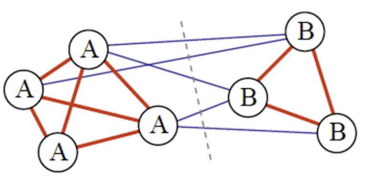
- Cut: 잘린 edge들의 weight 합
-> cut이 작다는 것은 픽셀들의 연관성이 약하다는 것으로 같은 그룹이 아닐 확률이 높은 것
-> 잘랐을 때 cut이 가장 작은 edge 집합을 찾아야함(Minimum cut)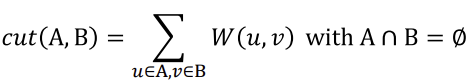
- Association: 그룹 edge의 합
-> cut이 작은 것 뿐만 아니라, 그룹 내부의 관계로 클수록 같은 그룹일 확률이 높다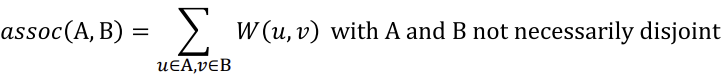
V: 모든 노드 집합

- A와 A 내부관계: Association
- A와 B 관계: Cut
- B와 B 내부관계: Association
2-2. Minimum cut
- 아래 식weight가 minimum이 되는 것의 cut
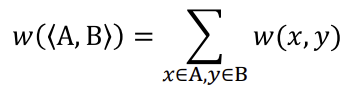
- 가장 달라보이는 선을 잘라 같은 그룹이 아닐 것 같은 집합 분리
- 그래프
G의 가장 작은 cut을 가지는 edge 집합S을 잘라 그래프의 연결 해제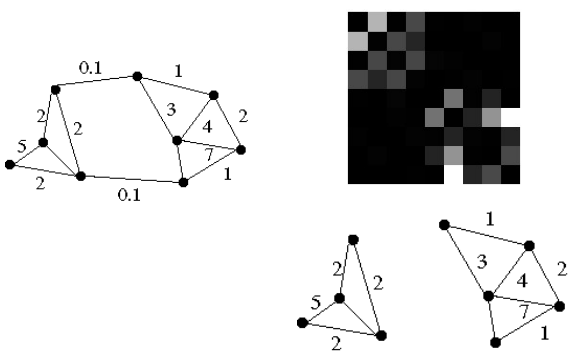
ex) 세 개의 자르는 과정 중 cut이 가장 작은 것으로 결정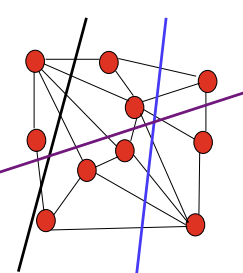
problem
- cut의 weight는 cut의 edges 수에 비례
- edge weight의 합이므로
작은 weight를 가지는 많은 edge들의 cut(Ideal cut)보다그렇게 작지 않은 하나의 edge의 cut이 더 작아서 잘못 자르는 현상 - 빨파를 분리하는 이상적인 분리가 아닌, 파란 무리의 약간 떨어진 애들만을 분리하여 빨파가 같은 그룹이 돼버림
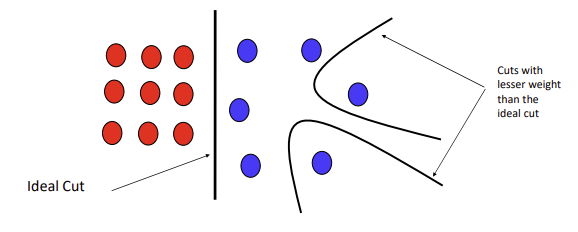
- edge weight의 합이므로
- affinity matrix의 eigen vetor로 비슷한 것을 찾을 수 있지만, 다른 무리임을 알아내기 어렵기 때문에 min cut을 진행했음
- 하지만, 하나만 잘린 파란색은 Association이 작다라는 것을 알 수 있음
- sol: normlaized cut
2-3. Normalized cut
- 다른 그룹과의 차이에 비교하여 그룹의 similarity를 최대화하기 위해 아래 식을 최소화
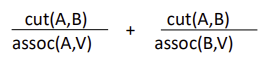
- 두 그룹의 Cut은 작아야지 다른 그룹일 확률이 크므로 최소화(분자)
- 각 그룹과 Assoc는 커야지 같은 그룹일 확률이 크므로 최대화(분모)
- 각 그룹과 graph의 나머지와의 Association에 비해 similarity가 크다. (그룹에 node를 더 추가하거나 삭제해선 안되는 최적 상태의 그룹, 위의 mincut의 문제를 해결해줌)
Problem (min cut, normalized cut 둘 다)
- 모든 엣지 조합을 다 해서 최소화하므로 np-complete문제.. 결국 approximation

- 시간이 오래 걸리므로 동영상같은 프레임단위 계산은 어렵고, 한 이미지에서 영역을 지정한 뒤 cut하는 경우가 많다