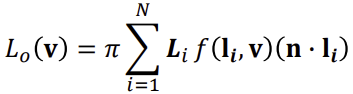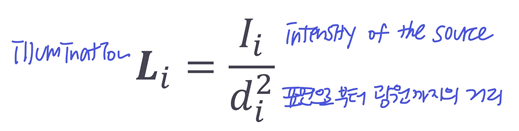[GPU프로그래밍] 6. Lighting and Shading

◾ Shading with multiple positional lights
- point lights
- 조명이 여러개 일때 vertex shader에서의 계산
- 각 조명들을 계산하고 합하여 총 intensity를 알아내기

- 여러개의 조명 정보(위치, 밝기)를 쉐이더 코드에 저장하기 위해 Uniform Arrays 사용
- 라이트 정보는 구조체로 이뤄짐 -> 구조체로 이뤄진 배열
- 5개의 조명으로 5번의 Phong model 계산한 결과를 전부 합쳐서 최종 컬러 내보냄

Unifrom Structure
- Uniform형태의 구조체에 값을 넘겨주기 위해서는 구조체의 멤버변수 따로따로 해주면 됨
(위의 예시에서는 구조체배열[5]이므로, 아래 과정을 5번 더 해주면 된다..)
◾ Shading with a directional light source
- Directional light: 아주 멀리 있는 빛이라 모든 버텍스에서 동일한 light vector를 가진다 (차이 거의X)
- 위치가 지정되는 point light와의 비교

- 표면의 모든 위치에서 light vector를 계산해줄 필요X
-> 계산 간단, 속도 증가
- 한 쉐이더 코드 안에서 Directional light와 Position Light를 조건문으로 나누어 계산
- LightPosition의
w가 0이면 위치가 아닌 벡터를 의미(homogeneous) -> directional light (머.. light 종류 매개변수를 Uniform으로 받아오든지 여러가지 방법이 있긴하죠)
(머.. light 종류 매개변수를 Uniform으로 받아오든지 여러가지 방법이 있긴하죠)
◾ Phong Shading (per-fragment shading)
- 라이팅을 vertex shader가 아닌 fragment shader에서 계산
- (per-vertex) Gouraud shading: vertex shader에서 라이팅 계산하여 얻은 버텍스 컬러들을 fragment shader에서 interpolation
- (per-fragment) Phong shading: vertex shader에서 normal과 position을 interpolation하고 fragment shader에서 그 값들로 셰이딩 계산
- per-vertex의 문제점
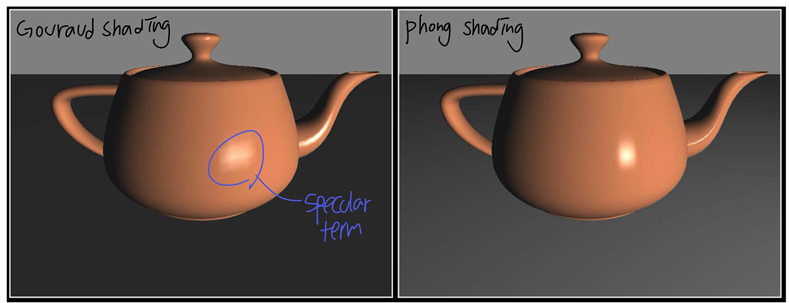
- 버텍스 컬러의 interpolation으로 칠해지기 때문에, Polygon안쪽에 specular term이 생겨 vertex가 영향을 못받는 경우에 specular가 잘 표현되지 못하고 어두워질 수 있음
-> 버텍스만으로 계산하기 때문에 Polygon이 넓으면 polygon 내부 라이트 표현이 잘 안될 수 있다
- Polygon 경계가 드러나기도 함
-> 셰이딩 퀄리티가 낮다
- 그래서 요즘은 거의 전부 per-fragment 셰이딩
◾ Phong Shading
- vertex shader에서는 light 계산에 필요한 Position, normal을 변환한 뒤 fragment shader로 넘겨줘야함
- Position과 normal은 camera coord로 변환
- gl-Position은 projection까지 하여 screen coord로 변환

- fragment shader에서 라이팅(phong model) 계산
- vertex shader에서 normal의 normalize를 해주긴 했지만, fragment shader로 넘어오는 interpolation과정에서 변화기 생겼을 수 있으므로 한번 더 normalize!

◾ Blinn-Phong reflection model
- phong model의 reflected vector
r보다 계산량이 적은 Halfway vector h를 사용하여 계산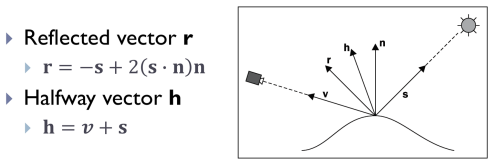
- phong model의 specular term식의
r만 h로 대체하면 됨
f: specualr의 퍼짐 정도 (클수록 좁고 밝음)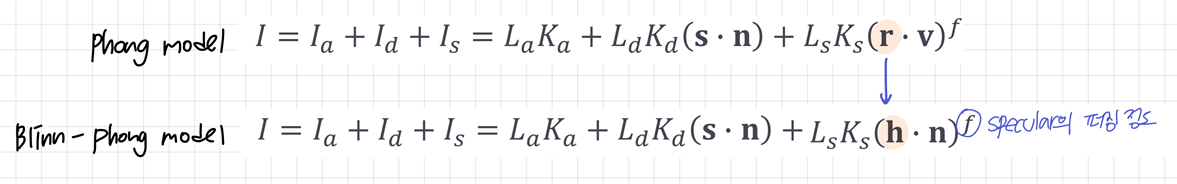
- 성능상의 이점을 가질 뿐만 아니라, 더욱 현실적으로 묘사


◾ Simulating a spotlight
- spotLight: 조명의 방향을 중심으로 일정 각도 안에만 조명 적용 (cone)
- 추가되는 조명 정보: 방향벡터
d, 각도c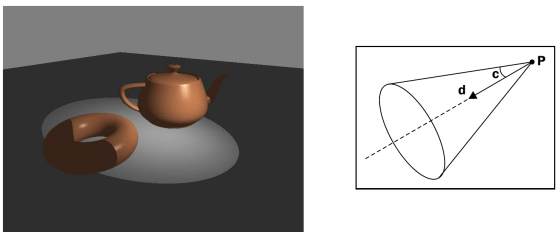
- Fragment shader에서 spotScale을 계산해주기
- 해당 position에서 spotLight까지의 벡터(뒤집어야 함)와 light방향벡터
d를 활용해서 각도를 구한다
- 각도가 light범위를 벗어나는지 확인하고, 벗어나지 않는 경우에 cos정도에 따라 spotScale을 지정해준다
- angle이 0에 가까울수록(= light방향벡터가 향하는 곳과 해당 버텍스가 가까울 때) cosAng이 1이고, 1인 cosAng에 exponetial해봤자 1이라서 spotScale은 1
- 반대로, angle이 90도에 가까워질수록 cosAng은 0에 가까워져 급격하게 어두워짐!
- 나머지는 Blinn-Phong 계산으로 동일

◾ Toon Shading (Cel Shading)
- 같은 구간에 있는 애들을 전부 같은 색으로 칠해주기 (quantization)
- 조건문 사용해서 밝기값으로 범위를 나누거나
- 조건문 없이 각도를 계산하여 범위를 나누거나 (아래 코드)

- 몇 구간으로 나눌건지에 대한 level을 설정
- sDotN에 level을 곱하고 내림 계산해서 구간을 만든다
0~0.9 -> 0 / 1~1.9 -> 1 / 2~2.9 -> 2 / 3 -> 3
- 그리고 다시 level으로 나누어서 [0, 1]이 되도록 한다
0 / 0.333... / 0.666... / 1- 이대로 Color값으로 사용

◾ Simulating Fog
- fragment 색 + (constant) fog 색
- fog색은 멀수록 많이
- 카메라 기준으로 멀수록 안보이니까 (이걸 계산)
- 원하는 렌더링 효과에 따라 Linear하게하거나 non-Linear하게 하거나..~
◾ Linear relationship Fog
- dmax: 안개 효과가 최대로 적용되는 거리
- dmin: 안개 효과가 최소로 적용되는 거리 (안개 효과X)
- z: 카메라로부터의 거리
- f: fag factor
- f=0 -> z=dmax (100% 안개)
- f=1 -> z=dmin (안개X)
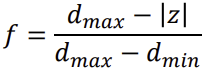
- fog factor를 사용해 fog color와 shade color를 mix

◾ Non-linear relationship Fog
- 좀만 떨어져도 잘 안보이게 (거리 비례X)
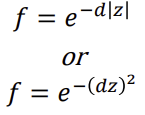
distance from camera
- fog뿐만 아니라 카메라로부터의 거리를 고려한 효과를 적용하는 경우
- 정확한 거리(in camera coordinate)
z가 아닌, length()함수를 사용하여 vertex position과 camera position(원점)의 거리를 계산
- 위처럼 하면 정확하지만,
length()함수는 sqaure root 연산을 포함하므로 계산이 큰 편
- 그래서 대략적인 거리인 depth
z를 사용하기도 한다 (결과가 별 차이 없으면 z쓰는게 좋음)
◾ Physically-Based Rendering
- Phong과 Blinn-Phong refelction model는 경험적 모델로 계산이 간단해서 자주 사용되지만, 물체가 많아지고 다양한 material을 고려하려면 조절할 매개변수가 너무 많아진다
-> physically-based refelection model을 사용
- 얘도 경험적 모델이지만, 물리법칙에 기반하기 때문에 더욱 정확하고, 일관성있게 파라미터 조절 가능
◾ reflection equation
- 빛이 표면에서 어떻게 분산되는가
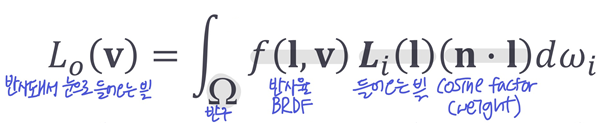
- 반구 범위의 적분은, 반구로 들어오는 모든 방향의 빛을 고려하기 위해 하는 것
- Lo(v): 반구로 들어오는 모든 방향의 입사광의 반사광 중 v방향으로 들어오는 빛의 양
- Li(l): 직접광만 고려할 수도 있고, 간접광도 같이 고려할 수 있는데 계산이 복잡해질 수 있다~
- 이때, cosine factor
(n•l)로 weight를 주며 적분 (노멀과 같은 방향으로 빛이 들어올 때 빛을 가장 많이 받으므로, cosine factor가 1일 때 가장 큰 weight를 준다) -> geometry of situation
- f(l,v): BRDF는 아래에서 자세히 살펴보자~
◾ BRDF (Bidirectional Reflectance Distribution Function)
f(l, v): l방향에서 들어온 빛이 v방향으로 얼만큼 반사되는가 (반사율)
- 입사하는 빛에 따른 반사하는 빛의 비율에 대한 함수
- 0~1범위의 (R, G, B)로 표현
- 수평, 수직 각도로 표현할 수 있기 때문에 방향만 고려했을 때 4d function으로 정의 (?)
- 몇가지 특이한 reflection model...~
- 1번과 6번 그림: 모든 방향으로 균일하게 반사 -> surface가 diffuse
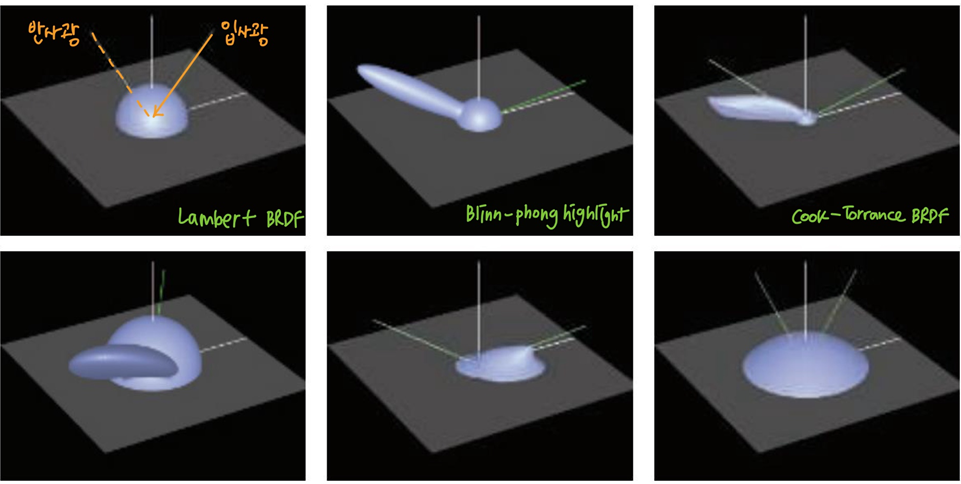
- 물질에 따라 BRDF가 다르므로, diffuse와 specular로 나뉜다
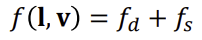
Diffuse BRDF
- diffuse한 surface는 난반사의 표현으로, 일부 빛은 표면으로 흡수되고 다시 표면을 나와 diffuse reflectance를 형성
- 모든 방향으로 균일하게 반사(방향성x) -> fd는 상수값을 가진다

- 물질마다 다른 값을 가짐
- 물체의 색을 결정 -> diffuse color cdiff
Microfacet theory
- 미세 표면 분포도에 따라 반사도 조절
- 표면은 아주 작은 거울 조각(small facets)들로 구성되어있고 다양한 방향을 바라보고 있다
- 표면이 매끄러우면 노멀 방향의 변화가 크지 않아서 반사광 방향이 거의 일정 -> 뚜렷
- 표면이 거칠면 노멀 방향의 변화가 커서 반사광 방향이 각각 다른 방향으로 분산 -> 흐릿

- 흐릿한 이유를 자세히 설명하자면, 특정 지점을 향한 입사광의 반사광이 분산돼서 일부가 눈에 들어오는데, 다른 지점을 향한 입사광의 반사광도 분산돼서 일부가 눈에 들어감 -> 여러 빛이 섞여 보여서 흐릿
- 실제로 버텍스를 조정하여 울퉁불퉁함을 구현하지 않고(평평하게 렌더링), 얼마나 울퉁불퉁한지 확률적으로 나타내서 계산하는 것 -> G, D
Specular BRDF
- 표면에 흡수되지 않고 바로 반사되는 빛 (glossy reflectance)
- Microfacet theory에 기반한 모델
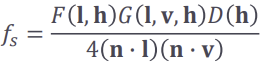
- Fresnel reflection
F(l, h)
- 평평한 표면(mirror)임을 가정한 물질마다의 반사 정도 -> 물질에 따라
- 노멀과 입사광 사이 각도에 따라 결정 (보는 각도에 따라 반사광이 다르게 보이기 때문)
- spcular는 눈으로 들어오는 방향 v만 고려해야하니까, 반사광의 방향이 v와 동일한 빛만 고려한다
-> 즉, v와 l의 halfway vector h와 노멀이 동일한 미세표면에 입사하는 빛의 비율을 따지면 반사 정도를 나타낼 수 있다! (반사광이 v와 같아서 눈으로 들어올테니까~)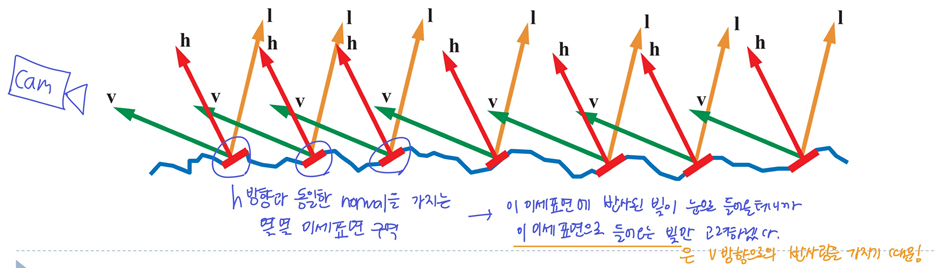
- Schlink approximation
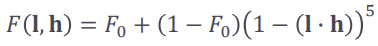
- F0: specular refletance의 특징 (상수값)
- F0인 이유는 노멀과 입사광 사이 각도가 0도일 때를 나타내고, 이때의 F0은 specular color로 사용
(금속은 diffuse fd가 없어 specular fs로만 컬러가 결정됨)
- 물질마다 F0의 경향성을 가진다 ( 금속은 F0이 크고, 비금속은 F0이 작음(0.05이하))
- RGB로 표현
- Metalness workflow (color)
- 금속: diffuse color가 없으므로 Cdiff=(0,0,0)으로 설정하고, spcular color F0을 컬러로 사용한다
- 비금속: specular color F0을 작은 값으로 설정하고 (ex.(0.04, 0.04, 0.04)), diffuse color Cdiff를 컬러로 사용한다
- Geometry function
G(l, v, h)
- micro surface에서 얼마나 가려지는지 -> 거칠기(microfacet)에 따라
- 가려지면 어두워짐 (occlusion)
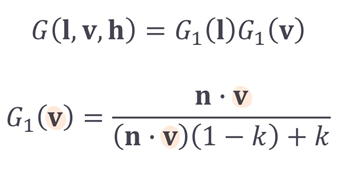
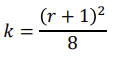
- 거칠기 파라미터 r로 상수 K를 계산하여 함수에 활용
- Microgeometry normal distribution function
D(h)
(microfacet distribution function)
- micro surface에서 normal vector가 얼마나 분산되어있는지 -> 거칠기(microfacet)에 따라
- 표면이 얼마나 울퉁불퉁할지를 확률적으로 나타낸 분포함수
- 넓을수록 거칠고, 좁을수록 매끈함
- 반사광의 방향이 v인 노멀의 방향이 h이라고 했고, 이 h 주변으로 normal이 많이 몰려있으면(분포함수가 좁고뾰족) 매끈
- specular highlight의 크기와 모양에 큰 영향
- GGX distribution
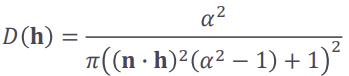
- α=r2
- 사용자가 조절하는 거칠기 파라미터 r를 바로 사용하지 않고, 제곱하여 α로 사용하는 이유는:
- 사용자가 조절하기 쉽도록 (조금 바꿨을 때 확 바뀌면 조절이 힘드니까)
- r을 그대로 사용하면 rough 범위가 좁아 활용 범위가 적음 (α는 real world와 비슷한 정도의 rough범위를 가짐)
 (위-α, 아래-r)
(위-α, 아래-r)
◾ Reflectance Equation (re)
- reflectance equation 식을 간단화하기 위해 들어오는 빛을 point light들로만 생각
- 적분할 필요 없이 point light source들의 합으로 나타내면 된다 -> multiple lights
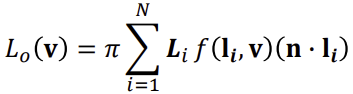
- 조명의 세기는 거리 제곱에 반비례하므로.. 아래 식까지 적용해주면 더 정확하다
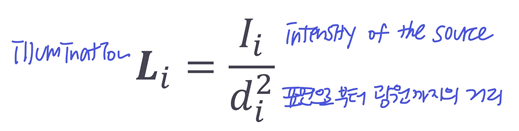
◾ material parameters
- non-physical-based shading보다 상대적으로 적고 직관적인 매개변수!!!!
- 금속/비금속 결정 (Boolean)
- roughness
r [0, 1]
- color (금속이면 F0, 비금속이면 Cdiff)
📃 Code



👀 위 결과 이미지의 Specular color를 살펴보면, 금속은 고유의 색을 가지고, 비금속은 하얀색으로만 나타남!





 (머.. light 종류 매개변수를 Uniform으로 받아오든지 여러가지 방법이 있긴하죠)
(머.. light 종류 매개변수를 Uniform으로 받아오든지 여러가지 방법이 있긴하죠)


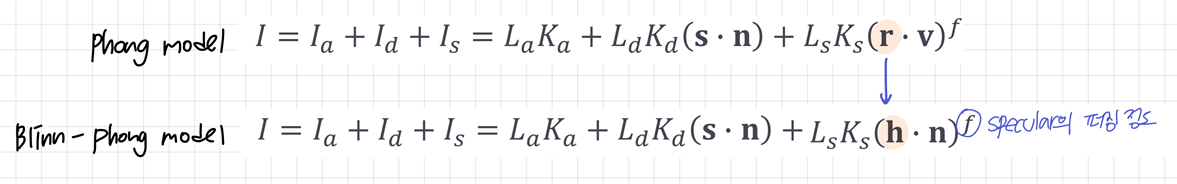






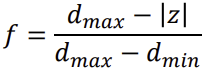

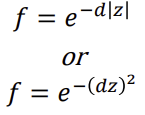

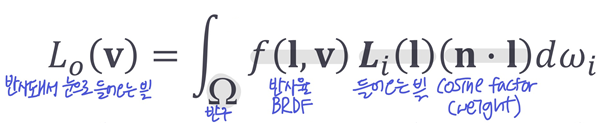

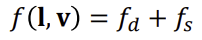

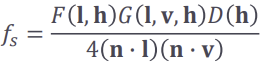

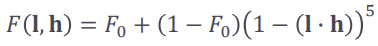
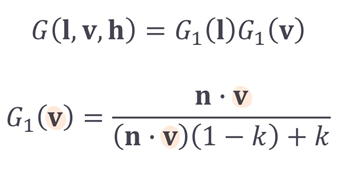
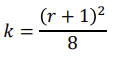
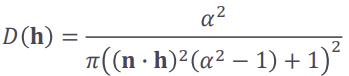
 (위-α, 아래-r)
(위-α, 아래-r)