📝 4주차

• 언리얼 머터리얼 강의 [Unreal Engine 5: One Course Solution For Material] Section2🔗
• 백준 단계별로 풀어보기🔗
• 백준 공통 문제🔗
  

📅 7월 30일 21:00-24:00

---

📖 언리얼

5. Lerp

• Linear Interpolate (L누르고 좌클릭)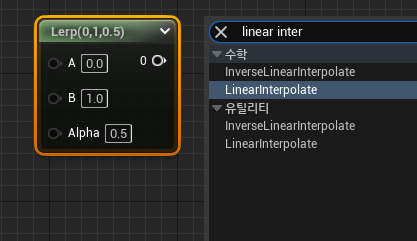
• Alpha가 0에 가까우면 A, 1에 가까우면 B값이 나타남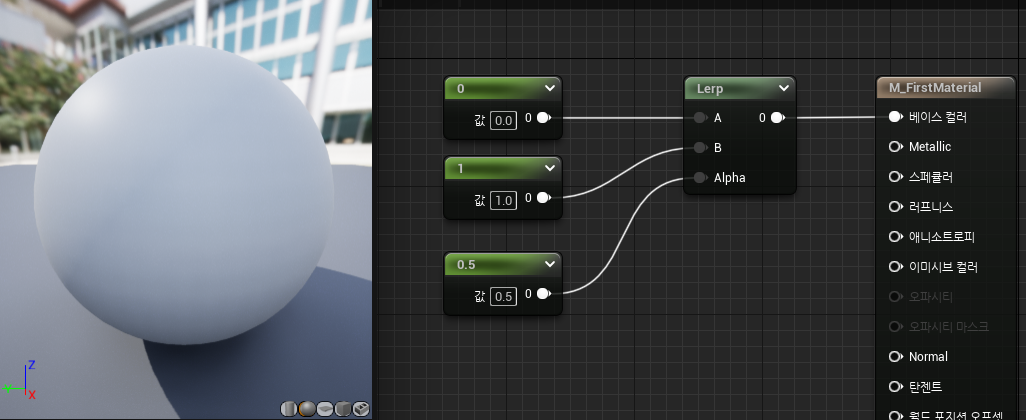
  

6. 텍스처 적용

• TextureSample 생성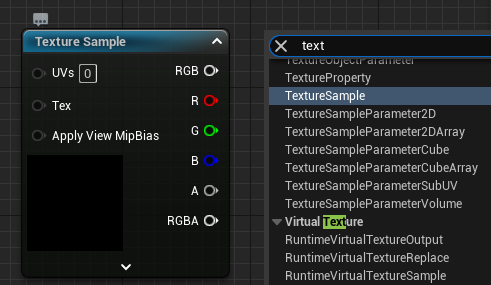
• 디테일 창에서 텍스처를 적용
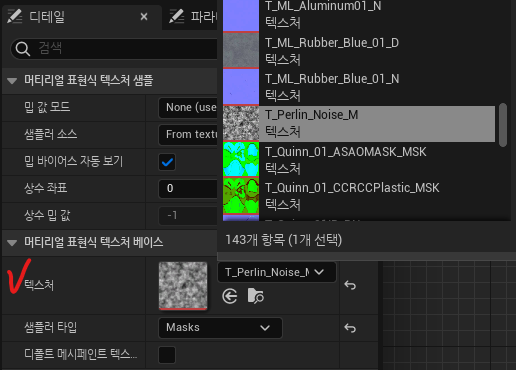
• 텍스처 우측 폴더모양 버튼을 누르면 콘텐츠브라우저에서 해당 텍스처의 위치를 찾을 수 있다.
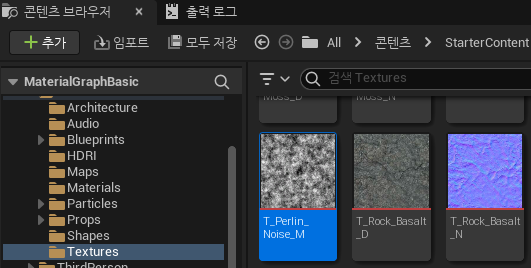
• 텍스처를 더블클릭하여 세부 정보를 확인할 수 있다.
• 각 채널에 따른 값도 확인할 수 있다. (해당 텍스처는 노이즈 텍스처로, 각 채널마다 같은 결과를 가진다.)
  

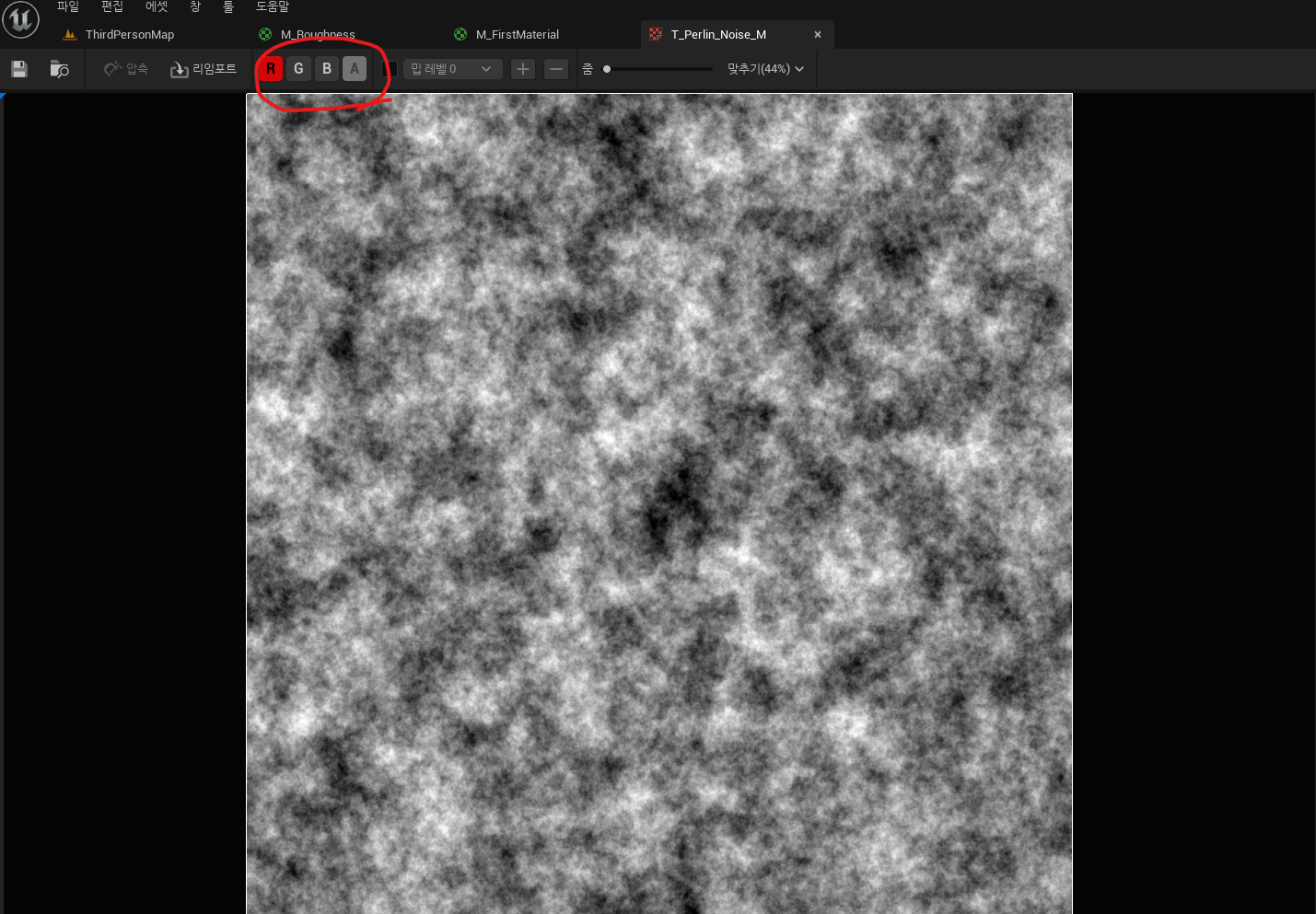
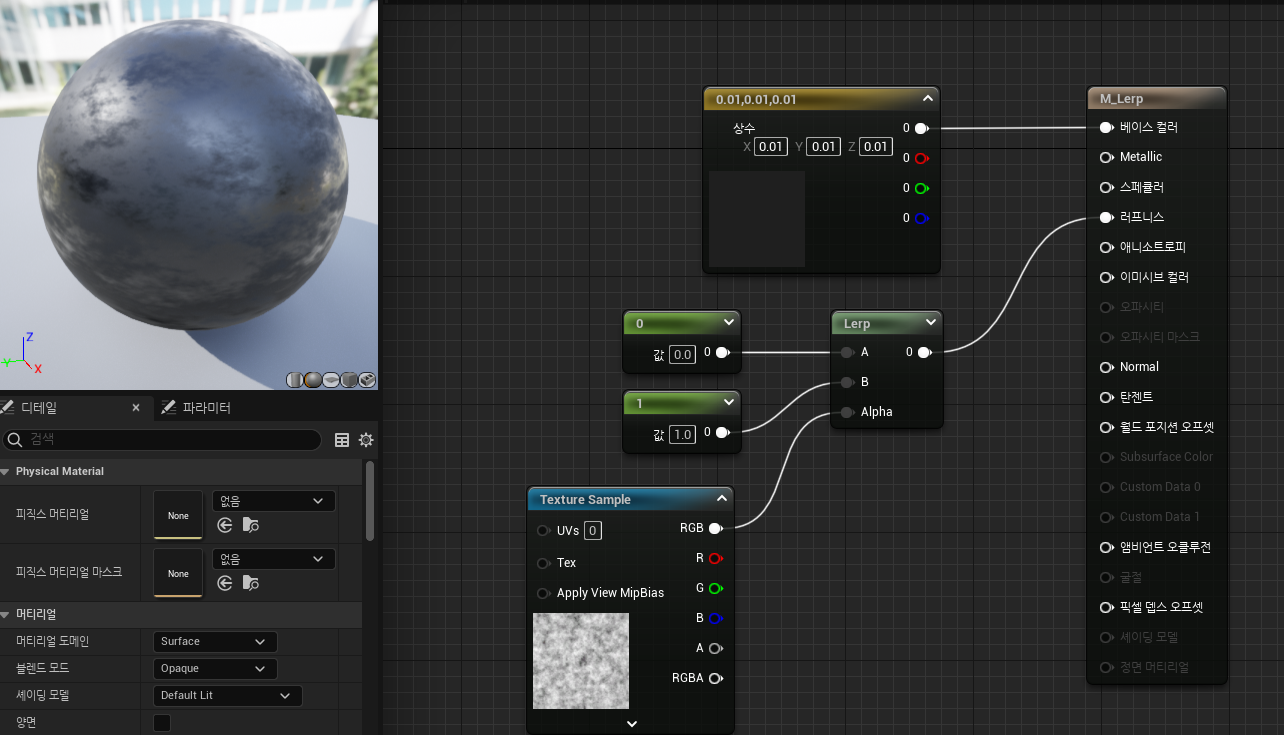
7. 노이즈 텍스처를 활용한 Lerp

• 노이즈 텍스처를 Lerp의 알파채널에 넣어 불규칙함을 표현
• 알파채널은 원벡터이고 노이즈 텍스처는 각 채널마다 같은 결과를 가지므로 R, G, B 중 아무 채널이나 사용해도 되지만 RGB자체를 넣어도 평균값으로 알아서 계산된다.
• 아래와 같이 적용하면 불규칙한 Roughness를 적용할 수 있다.
  

8. UV

• UV Mapping: 2D이미지를 3D모델의 표면으로 투영
• X, Y대신 U, V를 사용하여 나타낸 텍스처의 좌표
• Texture Coordinate를 생성하여 텍스처의 UV채널에 연결하여 텍스처의 패턴을 수정할 수 있다.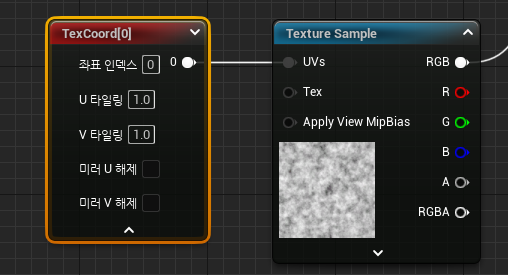
  

9. UV로 텍스처 크기 조절

• UV타일링이 커지면 패턴이 반복되어 작아지고, UV타일링이 작아지면 패턴이 확대되어 커진다.
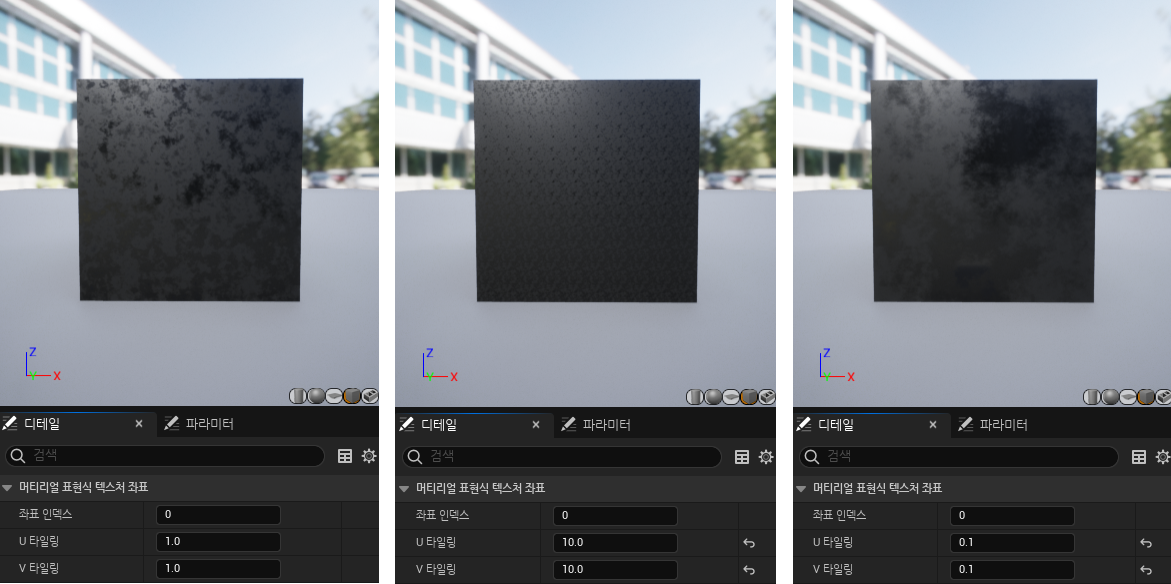
• Multiply를 활용하여 원벡터를 곱하면 UV타일링을 편하게 조절할 수 있다.
  (U, V에 같은 값이 곱해지므로 같은 비율로 크기가 조절된다.)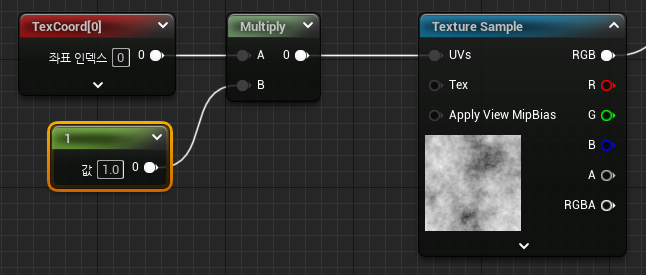
  

10. Component Mask

• 위의 Texture Coordinate는 원벡터 값을 반환
• 따라서 Component Mask를 활용해서 R, G마스크를 입혀서 U, V의 투벡터 값을 반환하게 한다.
• 또는, R, G 마스크를 따로 두어 U, V 각각의 원벡터를 반환하게하여 각 채널을 활용하기 쉽도록 할 수도 있다.
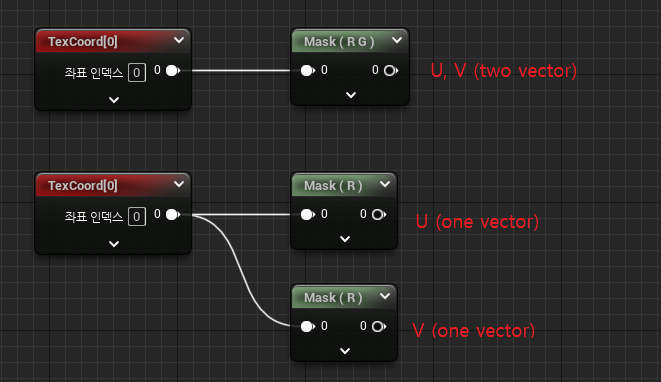
• 분리된 UV는 아래와 같이 가로/세로줄의 결과를 보인다.
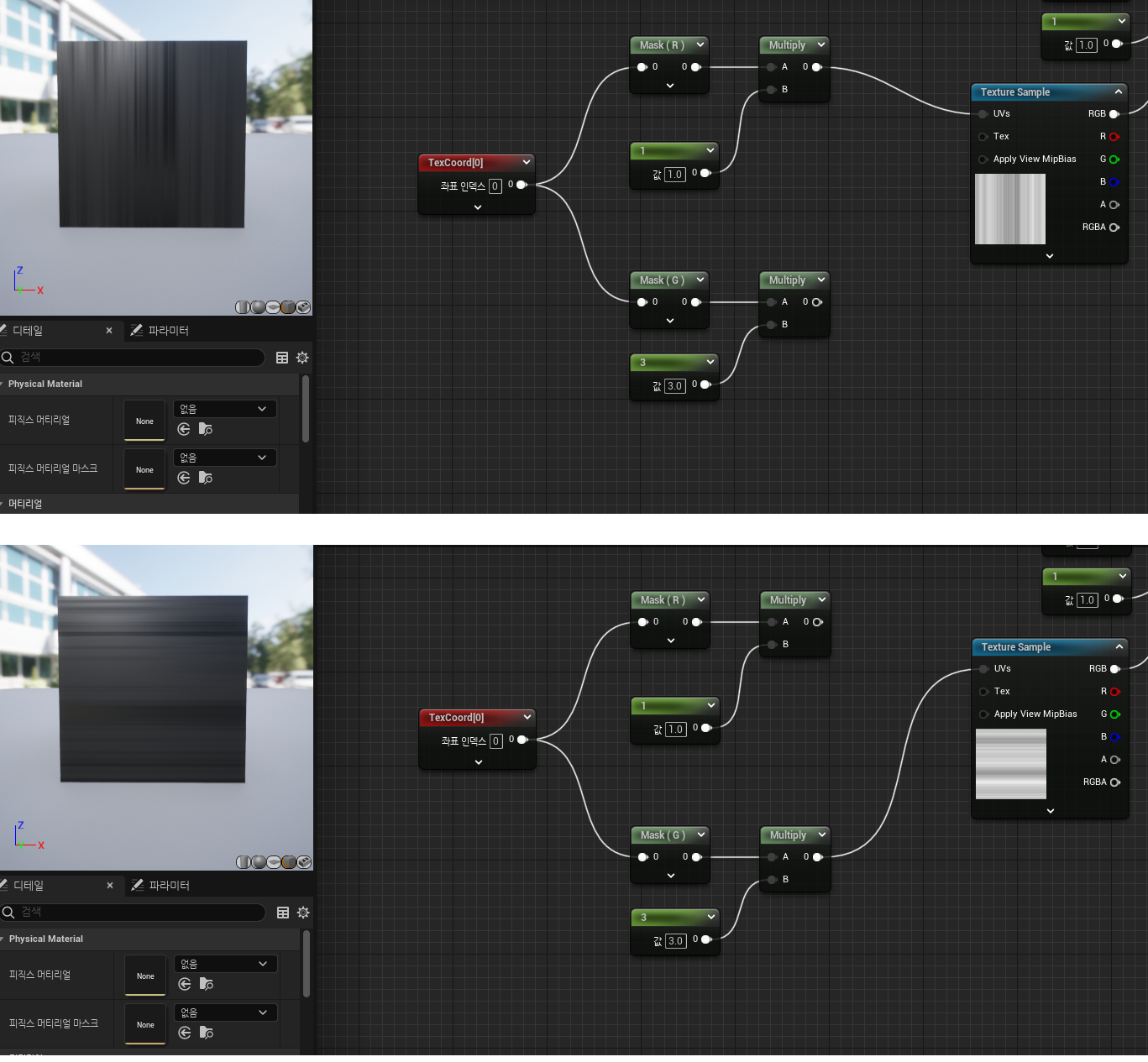
• 어쨋든 UV채널은 투벡터를 원하므로, 분리했던 UV를 AppendVector로 다시 합치면 된다.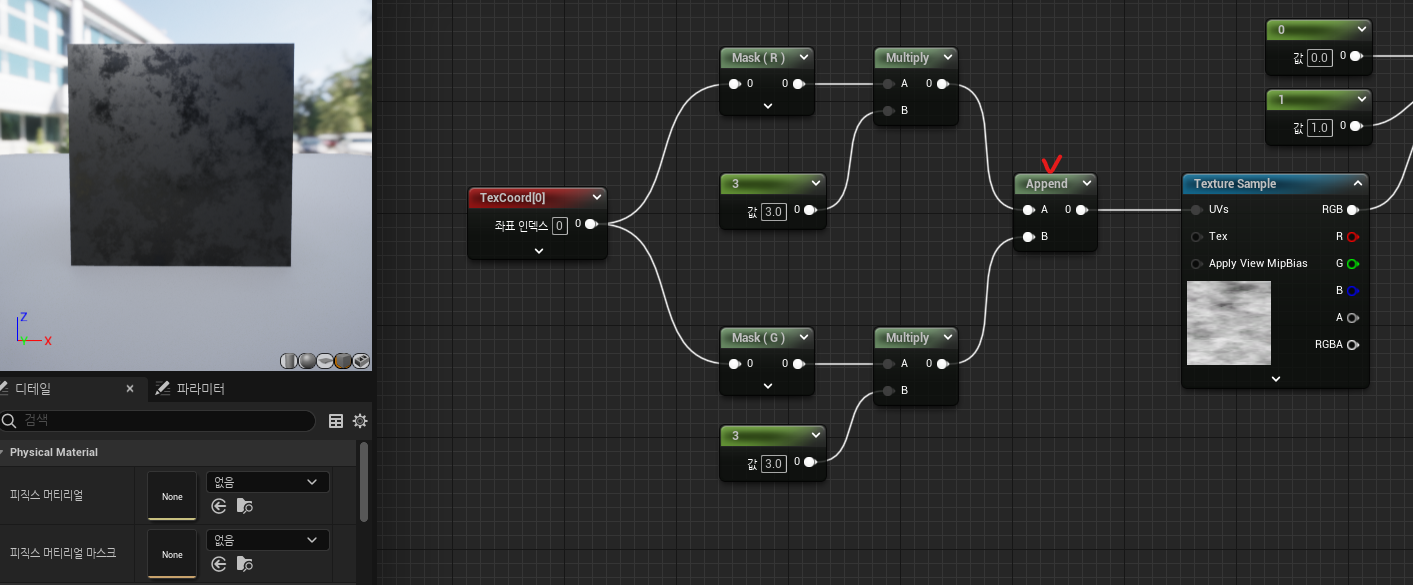
  

11. 텍스처 Import

• 콘텐츠 브라우저에서 우클릭하여 Import할 수 있다.

12.

---

📖 백준

◾ 동적 계획법 (Dynamic Programming) 🔗

(모든 예시는 피보나치 수열로 설명)

1. 동적 계획법 (DP)

• 분할 정복 패러다임 개념의 확장
• 최적화 문제를 해결하는 알고리즘
  -> 입력 크기가 작은 부분 문제를 해결한 후, 그 해들을 이용하여 큰 크기의 부분문제들을 해결 -> 최종적으로 원래 주어진 입력의 문제를 해결
• 큰 문제를 작은 문제로 쪼개서 그 답을 캐시에 저장해두고 재활용 (기억하며 풀기)

2. 사용 이유

• DP는 재귀 방식과 유사하다.
• 일반적인 재귀를 단순히 사용 시 동일한 작은 문제들이 여러 번 반복되어 비효율적인 계산이 될 수 있다. O(n^2)
• 그래서 한 번 구한 작은 문제의 결과 값을 저장해두고 재사용하는 것이다.O(f(n))

3. 조건

• 중복되는 부분 문제 (Overlapping Subproblems): 동일한 작은 문제들이 반복하여 나타나는 경우
• 최적 부분 구조 (Optimal substructure): 부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우

4. 종류

• 메모이제이션(Memoization): 하향식 접근 방법 -> 재귀
• 타뷸레이션(Tabulation): 상향식 접근 방법 -> 반복문

5. 단계

1. DP 필요 조건 분석
2. 문제의 변수 파악 n번째 숫자의 n
3. 점화식 f(n) = f(n-1) + f(n-2)
4. 메모: 변수 값에 따른 결과를 저장할 배열 필요
5. 기저 상태 파악: 가장 작은 문제의 상태 f(0)=0, f(1)=1
6. 구현: 메모이제이션과 타뷸레이션 중 하나의 방식으로 구현

🪧 24416 알고리즘 수업 - 피보나치 수1

• 주어진 피보나치 수 의사코드로 재귀호출과 동적계획법을 비교

#include <iostream>
#include <string>
using namespace std;

int memo[41] = { 0 };
int cnt1 = 0, cnt2 = 0;

int fib1(int n) {
	if (n == 1 || n == 2) {
		cnt1++;
		return 1;
	}
	else return (fib1(n - 1) + fib1(n - 2));
}

int fib2(int n) {
	memo[1] = memo[2] = 1;
	for (int i = 3; i <= n; i++) {
		cnt2++;
		memo[i] = memo[i - 1] + memo[i - 2];
	}
	return memo[n];
}

int main(int argc, const char* argv[]) {

	int n;
	cin >> n;
	fib1(n);
	fib2(n);

	cout << cnt1 << " " << cnt2;

	return 0;
}

🪧 {공통} 1149 RGB거리

• 색상 경우에 따른 누적 비용을 구해서 최소값을 찾는다.
• i번째 집의 누적 비용은 [현재 집의 색과 겹치지 않는 색상]의 i-1번째 집들 중 최소값과 현재 집에 필요한 색상의 비용을 더한다.

#include <iostream>
using namespace std;

int rgb[1001][4]; //비용
int dp[1001][4]; //누적 비용

int findMinCost(int n) {

	int tempMin; //이전 집과 겹치치 않는 색상 중 최소 비용

	for (int i = 1; i <= n; i++) { //모든 집 탐색
		for (int j = 1; j <= 3; j++) { //각 집의 색상 별 비용 탐색
			
			if (i == 1) { //1번 집은 이전 집이 없으므로 색상 별 비용으로 갱신
				dp[i][j] = rgb[i][j];
			}
			else {
				//i번째 집을 빨간색(j=1)으로 칠하는 경우의 tempMin
				if (j == 1) tempMin = min(dp[i - 1][j + 1], dp[i - 1][j + 2]);

				//i번째 집을 초록색(j=2)으로 칠하는 경우의 tempMin
				else if (j == 2) tempMin = min(dp[i - 1][j - 1], dp[i - 1][j + 1]);

				//i번째 집을 파란색(j=3)으로 칠하는 경우의 tempMin
				else if (j == 3) tempMin = min(dp[i - 1][j - 1], dp[i - 1][j - 2]);

				//tempMin과 해당 색상의 비용의 합
				dp[i][j] = tempMin + rgb[i][j];

			}
		}
	}

	//마지막 집의 3가지 누적 비용 중 최소 비용 반환
	tempMin = min(dp[n][1], dp[n][2]);
	return min(tempMin, dp[n][3]); 
}


int main(int argc, const char* argv[]) {

	int n;
	cin >> n;

	//각 집마다의 비용 저장
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= 3; j++) {
			cin >> rgb[i][j];
		}
	}
	
	cout << findMinCost(n);
	return 0;
}

🪧 10811 바구니 뒤집기

• 두 수가 같지 않은 경우 y-x+1/2만큼 반복하며 x+j, y-j를 바꾼다.
• 1, 4 입력한 경우 -> arr[1]과 arr[4], arr[2]와 arr[3]를 바꾸는 두 번의 swap 실행

#include <iostream>

using namespace std;

int main(int argc, const char* argv[]) {

	int N, M;
	int x, y;

	cin >> N >> M;

	int* arr = new int[N+1];

	for (int i = 1; i <= N; i++) {
		arr[i] = i;
	}

	for (int i = 0; i < M; i++) {
		
		cin >> x >> y;
		
		if (x != y) {
			for (int j = 0; j < (y - x + 1)/2; j++) {
				swap(arr[x + j], arr[y - j]);
			}
		}
	}

	for (int i = 1; i <= N; i++) {
		cout << arr[i] << " ";
	}

	return 0;
}

🪧 2743 문자열

#include <iostream>

using namespace std;

int main(int argc, const char* argv[]) {
string S;

	cin >>S;
	
	cout << S.length() << endl;

	return 0
}

🪧 9086 바구니 뒤집기

#include <iostream>

using namespace std;

int main(int argc, const char* argv[]) {
	int T;
	string S;

	cin >> T;

	while (T--) {
		cin >> S;
		cout << S[0] << S[S.length() - 1] << endl;
	}

	return 0;
}

🪧 5622 다이얼

• 문자를 아스키코드로 변환하고 65를 빼서 A->0이 되도록 변환
• 변환한 수를 3으로 나눴을 때 몫+3을 하여 시간을 구한다.
• PQRS로 생긴 예외: P(15), Q(16), R(17)는 3으로 나눴을 때 몫이 5이지만 S(18)은 몫이 6이므로 S인 경우에는 -1을 해줘야한다.
• 위와 동일한 이유로 그 이후의 값 TUV의 V(21), WXYZ의 Y(24), Z(25)도 -1을 해줘야한다.

#include <iostream>

using namespace std;

int main(int argc, const char* argv[]) {
	string S;
	int time = 0;

	cin >> S;

	for (int i = 0; i < S.length(); i++) {
		time += ((int)S[i] - 65) / 3 + 3;
		if (S[i] == 'S' || S[i] == 'V' || S[i] == 'Y' || S[i] == 'Z') time--;
	}

	cout << time;
	return 0;
}

🪧 11718 그대로 출력하기

• 공백을 포함한 한 줄을 입력받는 경우에는 cin 대신 getline(cin, S)을 사용
• 입력 값이 없는 경우는 ""로 저장되므로, 이 경우에 반복문이 끝나도록 하였다.

#include <iostream>
#include <string>

using namespace std;

int main(int argc, const char* argv[]) {
	string S;

	while (true) {
		getline(cin, S);
        
		if (S == "") break;
		
		cout << S << endl;
	}
	

	return 0;
}