[셰이더 프로그래밍 입문] Part1 | 셰이더 프로그래밍 기초 (Chapter3~4)

jungizz_·2023년 4월 6일

Shader Programming

목록 보기

2/5

Chapter 3 | 텍스처매핑

🆕 HLSL

sampler2D - 텍스처에서 텍셀을 구해올 때 사용하는 샘플러 데이터형

tex2D() - 텍스처 샘플링에 사용하는 HLSL 함수

swizzle - 벡터 성분의 순서를 마움대로 뒤섞을 수 있는 방법

◾ 텍스처매핑과 UV좌표

3D물체를 구성하는 삼각형의 각 정점을 텍스처 위에 있는 한 픽셀에 대응시켜준다.
백분율(0~1)을 사용하여 텍스처 위의 한 픽셀을 가리킨다.
x, y와 구별하기 위해 UV를 사용한다.
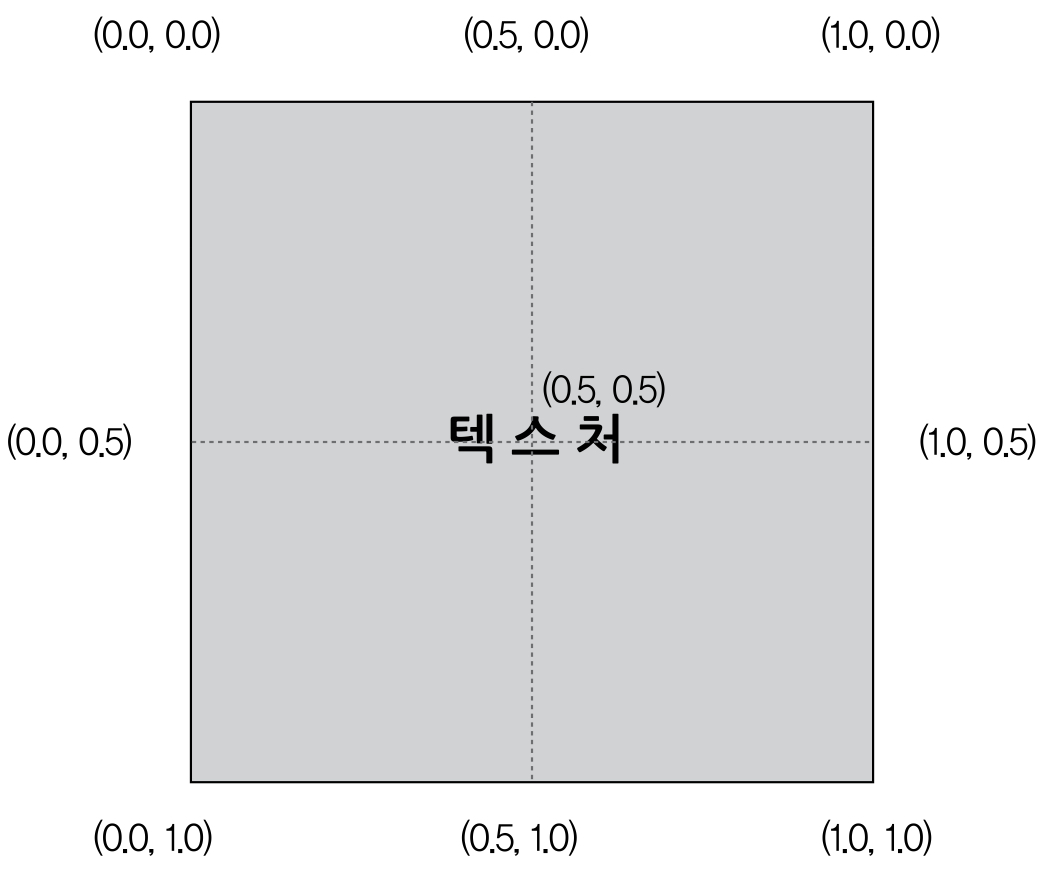
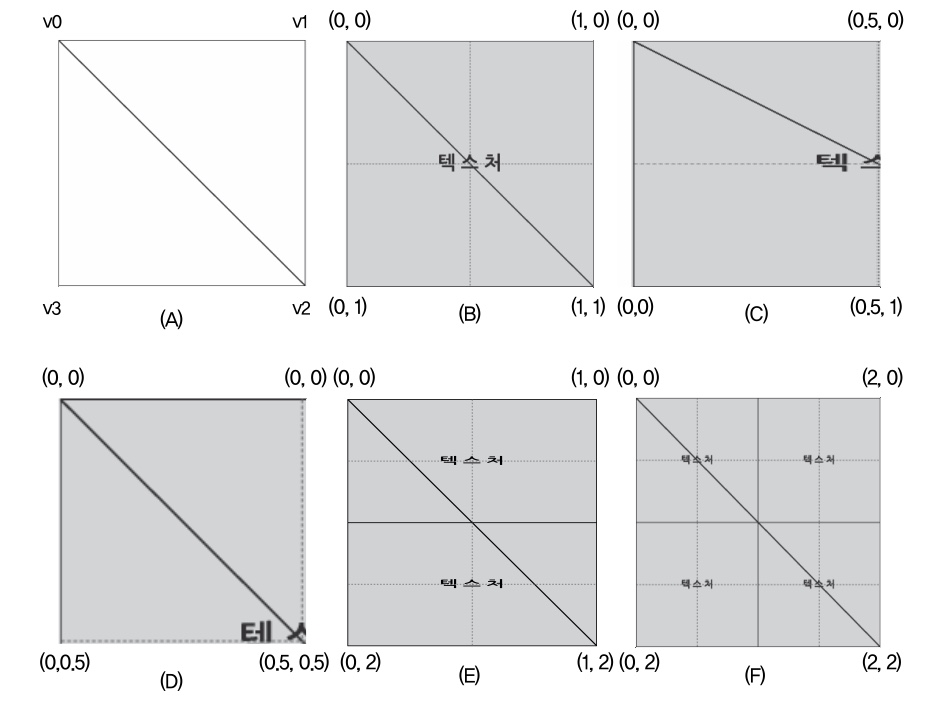
적절한 UV좌표를 대입하여 텍스처매핑을 한다.

📝 기초설정

TextureMapping 셰이더를 생성하고 이전과 동일하게 행렬들을 추가한다.
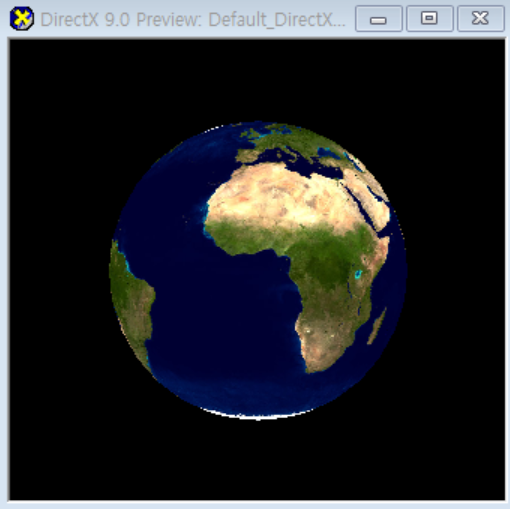
텍스처로 사용할 이미지(earth.jpg)를 추가하고 이름을 DiffuseMap으로 변경한다.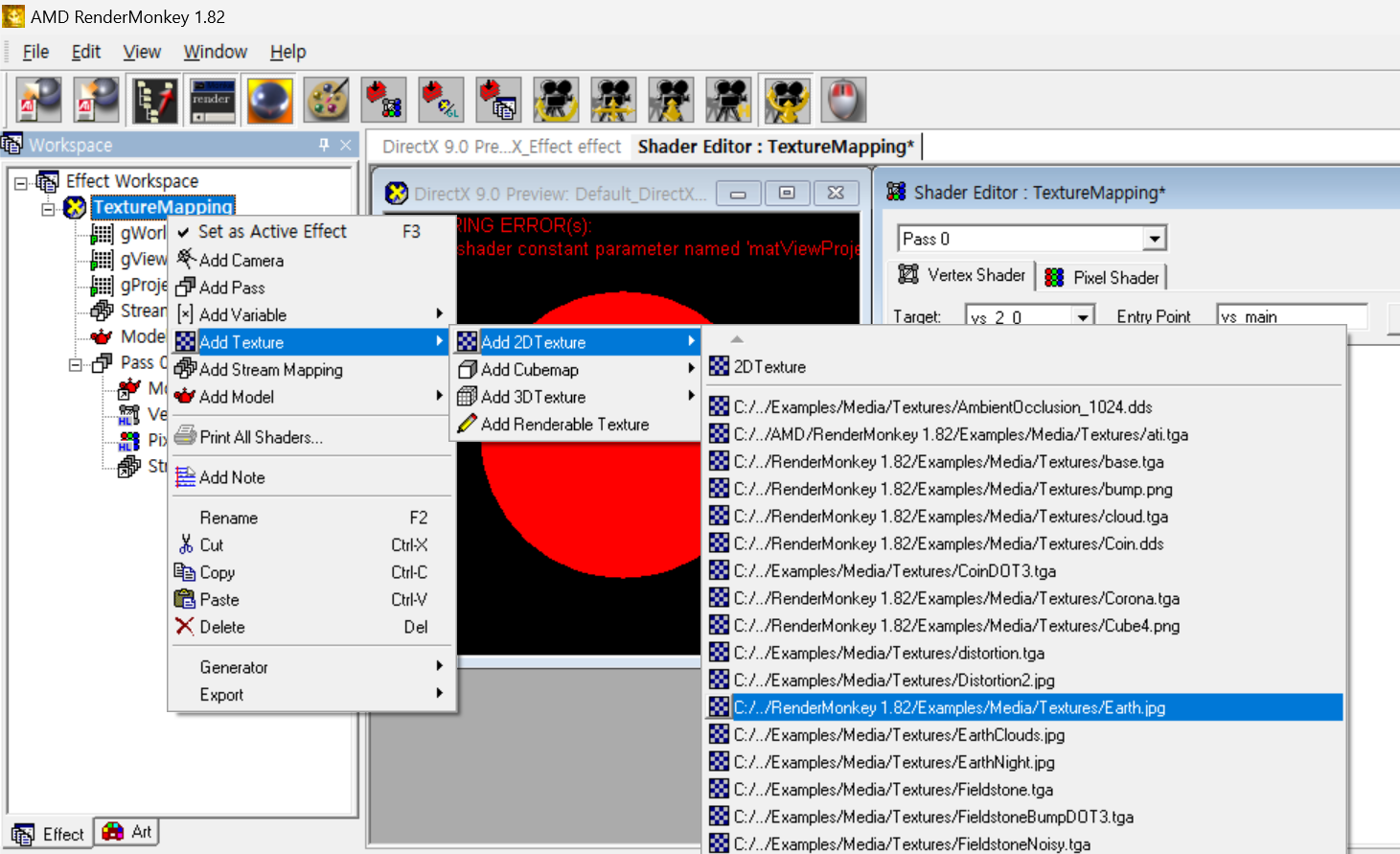
Pass0을 오른쪽 클릭해서 텍스처오브젝트를 추가하고 이름을 DiffuseSampler로 변경한다.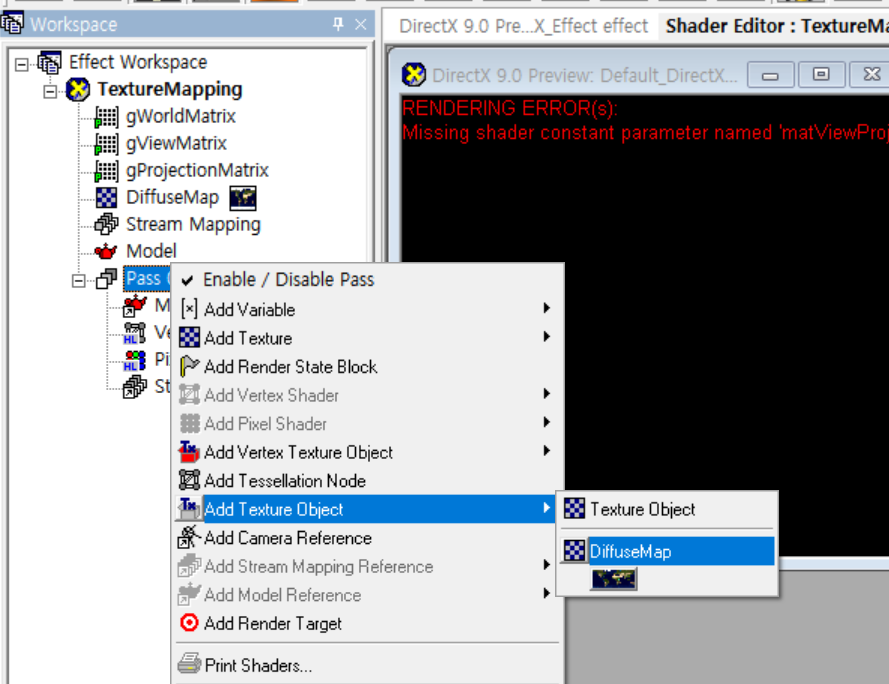

텍스처를 입히는 작업(텍스처매핑)은 표면을 구성하는 모든 픽셀에 입히는 것이기 때문에 각 픽셀마다 호출되는 픽셀셰이더에서 해야된다.

UV좌표는 각 정점마다 지정해야되기 때문에 전역변수가 아닌 정점데이터의 일부로 전달된다.

📝 정점셰이더 코드

1. 입력데이터

UV좌표의 데이터형은 float2이고 TEXCOORD 시맨틱을 가진다.

struct VS_INPUT{
 float4 mPosition : POSITION;
 float2 mTexCoord : TEXCOORD0; //UV좌표 (TEXCOORD의 수가 여러개이므로 0을 붙임)
};

2. 출력데이터

정점셰이더에서는 레스터라이저를 위한 위치정보 말고도 픽셀셰이더를 위해 UV좌표를 반환할 수 있다.

struct VS_OUTPUT{
 float4 mPosition : POSITION;
 float2 mTexCoord : TEXCOORD0; //UV좌표 반환
};

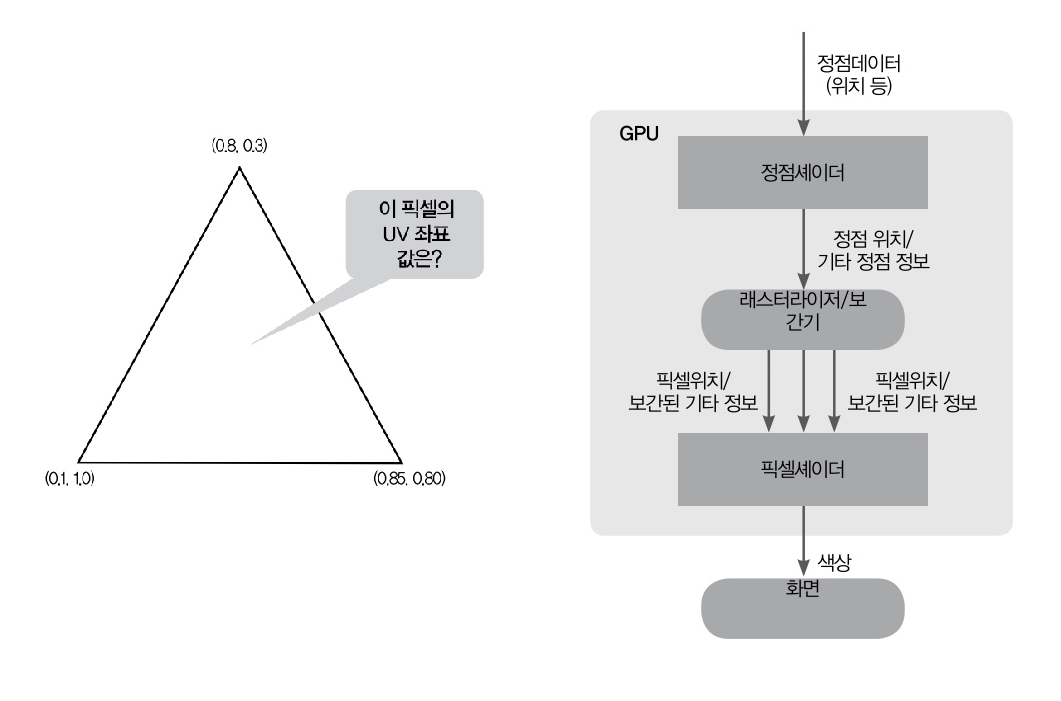
☑️ 보간기

픽셀의 UV좌표는 정점의 UV좌표와 다른 것이 대부분이다.

픽셀의 올바른 UV좌표를 구하기 위해서 세 정점까지의 거리의 비율에 따라 UV값을 혼합한다. 이것을 보간기Interpolator가 처리한다.

3. 전역변수

float4x4 gWorldMatrix;
float4x4 gViewMatrix;
float4x4 gProjectionMatrix;

4. 함수

UV좌표는 3차원 공간에 존재하는 것이 아니라, 삼각형의 표면상에 존재하기 때문에 Output구조체에 전달만 해준다.

VS_OUTPUT vs_main(VS_INPUT Input){
 VS_OUTPUT Output;

 Output.mPosition = mul(Input.mPosition, gWorldMatrix);
 Output.mPosition = mul(Output.mPosition, gViewMatrix);
 Output.mPosition = mul(Output.mPosition, gProjectionMatrix);

 Output.mTexCoord = Input.mTexCoord; //UV좌표 전달
 return Output;
}

📝 픽셀셰이더 코드

텍스처 이미지에서 텍셀texel을 구해와 그 색을 화면에 출력하기

1. 입력데이터 및 전역변수

텍스처로 사용할 이미지와 현재 픽셀의 UV좌표

sampler2D DiffuseSampler; //미리 만들어둔 텍스처 오브젝트

struct PS_INPUT{
 float2 mTexCoord : TEXCOORD0; //정점셰이더로부터 보간기를 거쳐 들어온 UV좌표
};

❗픽셀셰이더의 입력데이터 = 정점셰이더의 출력데이터

2. 함수

보간기가 계산해준 UV좌표를 받기 위해 PS_INPUT Input 매개변수 필요
tex2D 내장 함수를 사용해 텍셀 값 구하기

float4 ps_main(PS_INPUT Input): COLOR{
 float4 albedo = tex2D(DiffuseSampler, Input.mTexCoord); //UV값과 텍스처 샘플러로 텍셀 값 구하기
 return albedo.rgba;
}

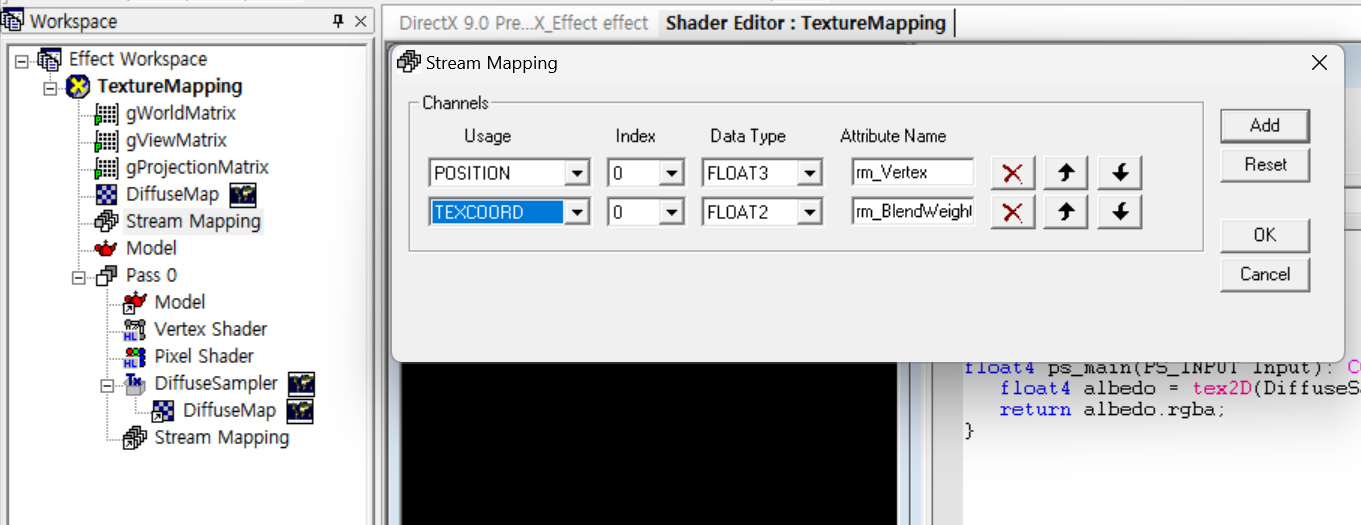
☑️ 정점버퍼에서 올바른 UV좌표 값으로 불러오기

Stream Mapping을 더블클릭하여 TEXCOORD 항목을 추가한다.

F5를 눌러 결과를 확인한다.

➕ Swizzle

HLSL에서 벡터형 변수 뒤에 xyzw, rgba 등의 접미사로 벡터의 성분에 접근하는데, xyzw, rgba의 순서를 바꿔가면서 벡터의 성분에 접근할 수 있다.

// rgb값만 가져오기
float3 rgb = albedo.rgb;

//rgb채널의 순서 바꾸기
float4 newAlbedo = albedo.bgra;

//특정 채널만 반복
float4 newAlbedo = albedo.rrra;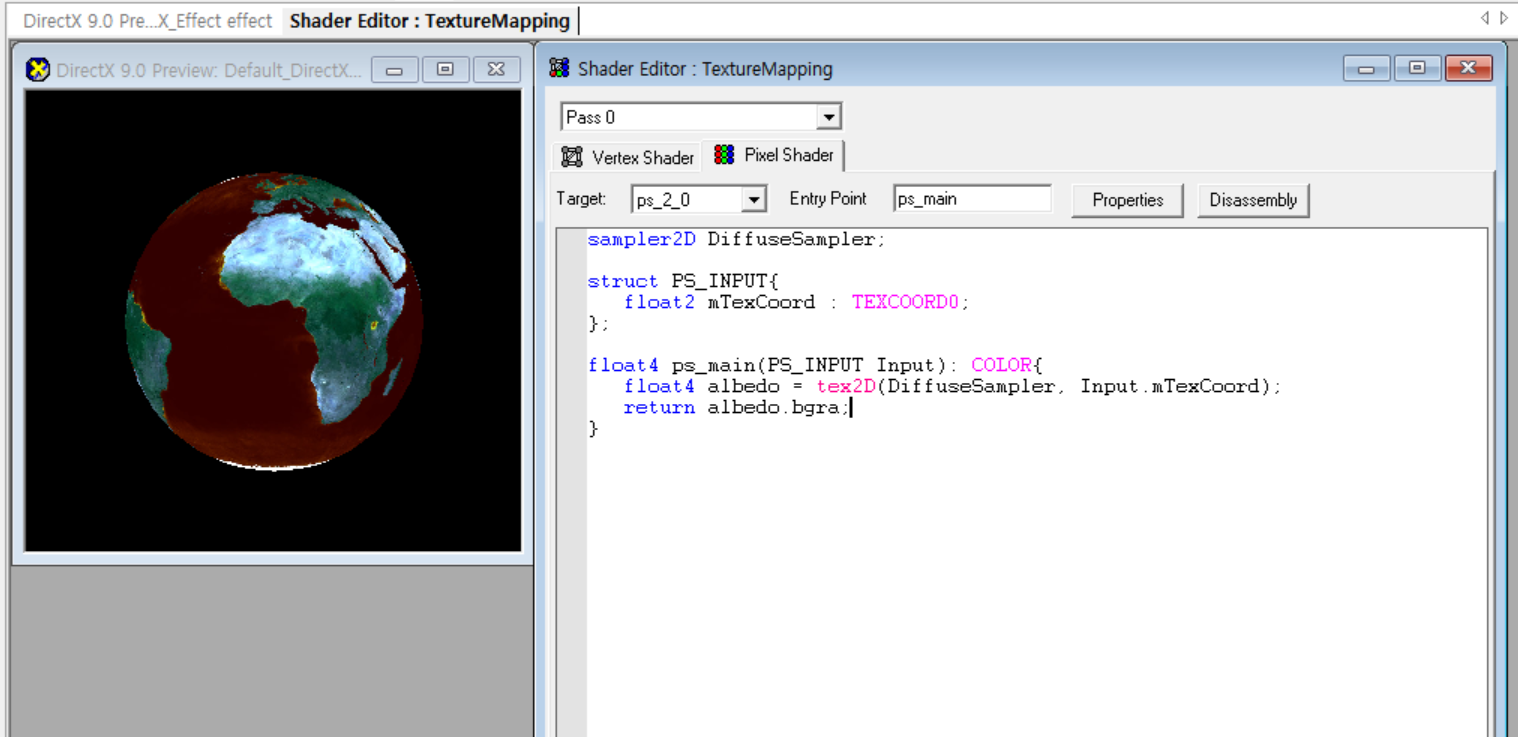

◾DirectX 프레임워크

Chapter 4 | 기초적인 조명셰이더

🆕 HLSL

NORMAL - 정점의 법선정보를 불러올 때 사용하는 시맨틱

normalize() - 벡터 정규화 (단위벡터로 만들기)

dot() - 내적

saturate() - 0~1을 넘어서는 값의 범위를 자름

reflect() - 벡터반사

pow() - 거듭제곱

❗간접광(전역조명모델)과 직접광(지역조명모델) 중에서 직접광만 다뤄본다.

◾ 빛의 구성 요소

난반사광
정반사광

◾ 난반사광 `diffuse Light`

여러 방향으로 고르게 반사되는 빛
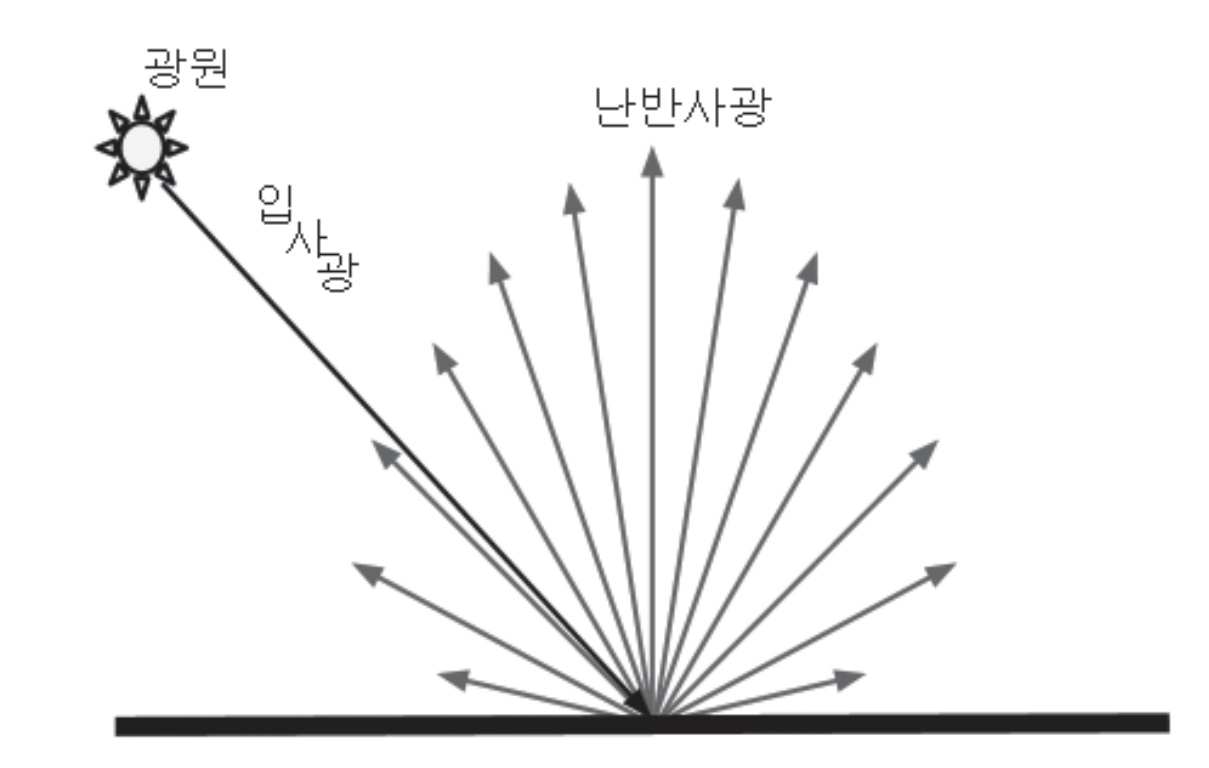
물체의 표면이 거칠수록 난반사가 심해진다.

☑️ 람베르트 모델 Lambert

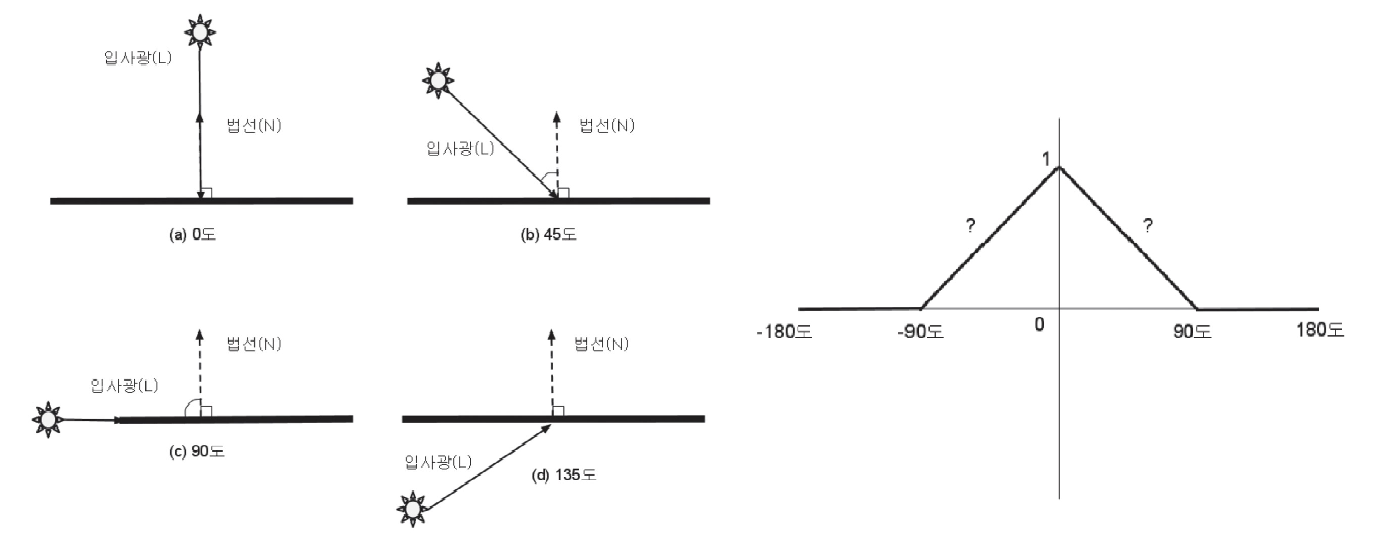
표면법선과 입사광이 이루는 각의 코사인 값이 난반사광의 양이다.

0도일때 가장 밝고cos0=1, 90도일때 가장 어둡다cos90=0.

그 이후로도 음수값이므로 어둡다.

빛의 밝기 그래프

셰이더에서 코사인 함수를 매번 호출하는 것의 대안으로 내적연산이 있다.

표면법선A(a, b, c)과 입사광B(d,e,f)의 단위벡터를 내적하면 두 벡터를 이루는 각의 코사인값을 구할 수 있다.
cosΘ=|A'|·|B'| = (a x d) + (b x e) + (c x f)

📝 기초설정

Lighting 셰이더를 생성하고 이전과 동일하게 행렬들을 추가한다.
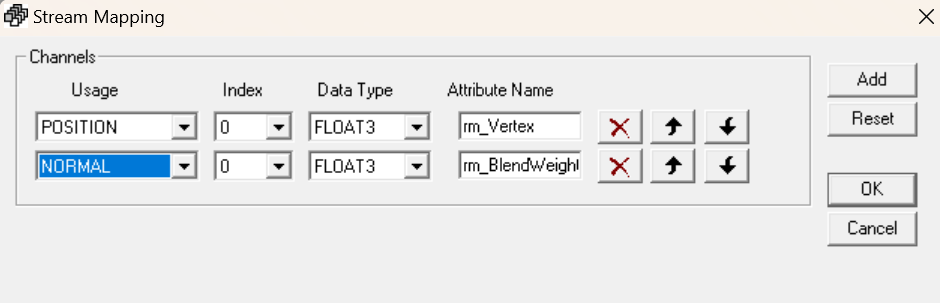
정점버퍼로부터 법선정보를 가져오기 위해 위에서 UV정보를 가져온 것 처럼 NORMAL 필드를 추가한다.
광원의 위치에서 현재 픽셀위치까지의 직선이 입사광의 벡터이다. 입사광의 벡터를 구하기 위해 광원의 위치만 알면 되기 때문에 월드에서 전역변수gWorldLightPosition를 만든다. 변수명을 더블클릭해 광원의 위치를 (500, 500, -500, 1)로 설정한다.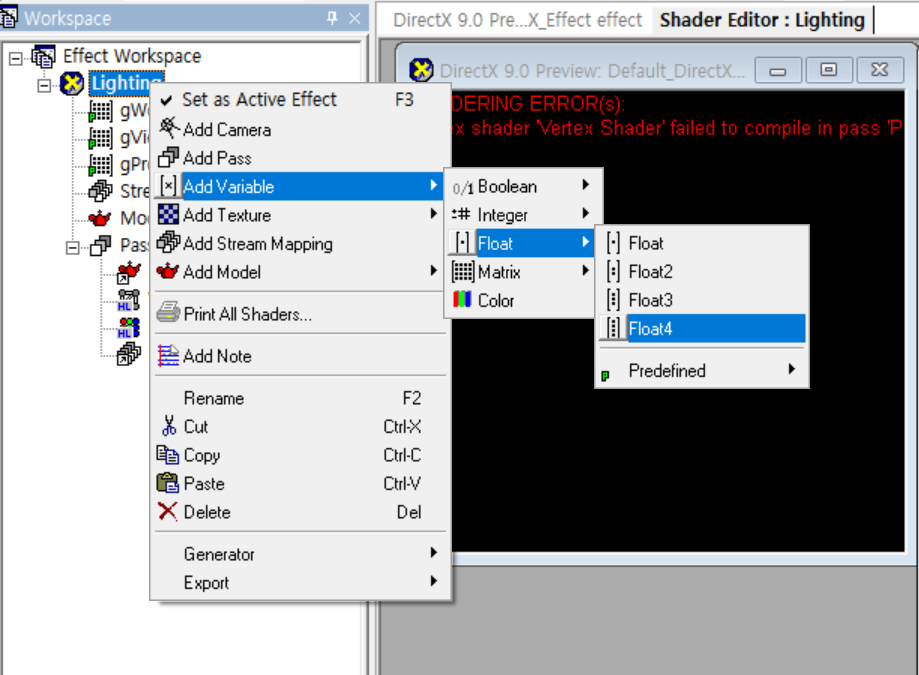

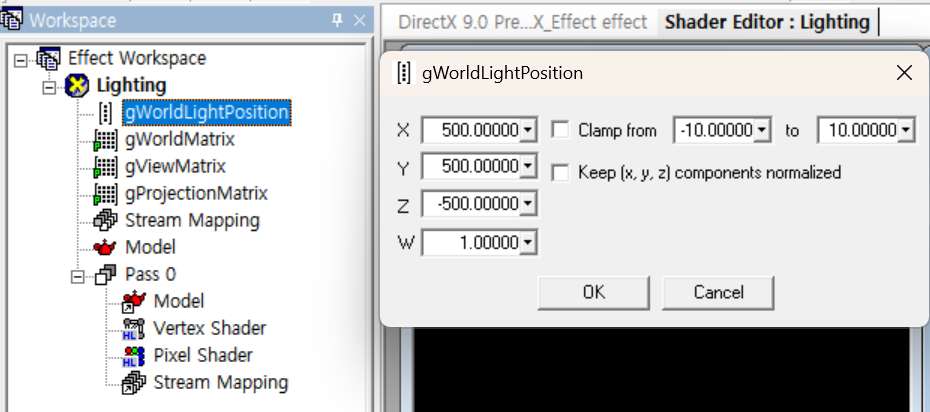
📝 정점셰이더

1. 전역변수

float4x4 gWorldMatrix;
float4x4 gViewMatrix;
float4x4 gProjectionMatrix;

float4 gWorldLightPosition; //광원의 위치

2. 입력데이터

struct VS_INPUT{
   float4 mPosition : POSITION;
   float3 mNormal : NORMAL; //법선벡터
};

3. 출력데이터

내적의 결과값은 스칼라이다. 하지만 나중에 이 값을 픽셀의 RGB값으로 출력할 것 이므로 mDiffuse는 float가 아닌 float3으로 선언한다.
mDiffuse 용도에 딱 맞는 시맨틱은 없다. 이런 경우 보통 TEXCOORD 시맨틱을 사용한다.

struct VS_OUTPUT{
   float4 mPostition : POSITION;
   float3 mDiffuse : TEXCOORD1 //내적의 결과 (난반사광)
};

4. 함수

❗ 동일한 계산을 픽셀셰이더와 정점셰이더 둘 다에서 할 수 있다면 정점셰이더에서 하는 것이 성능상 유리하다.

입사광 벡터는 현재위치에서 광원위치를 빼서 구한다. 광원의 위치가 월드공간이므로 월드행렬을 곱한 직후의 Output.mPosition를 사용해야한다.

VS_OUTPUT vs_main(VS_INPUT Input){
   VS_OUTPUT Output;
   
   Output.mPosition = mul(Input.mPosition, gWorldMatrix); 
   
   float3 lightDir = Output.mPosition.xyz - gWorldLightPosition.xyz; //입사광 벡터
   lightDir = normalize(lightDir); //벡터의 길이 1로 만드는 정규화

법선벡터는 정점버퍼에서 곧바로 오는 데이터이므로 물체공간에 있다. 3D연산을 위해 월드공간으로 변환한다. (입사광벡터와 통일)

   Output.mPosition = mul(Output.mPosition, gViewMatrix);
   Output.mPosition = mul(Output.mPosition, gProjectionMatrix);
   
   //법선벡터를 월드공간으로 변환, Input.mNormal이 float3이므로 월드행렬을 3x3행렬로 캐스팅하여 계산한다.
   float3 worldNormal = mul(Input.mNormal, (float3x3)gWorldMatrix); 
   worldNormal = normalize(worldNormal); //정규화

내적 구하기 (-lightDir를 사용한다.)

   Output.mDiffuse = dot(-lightDir, worldNormal); //내적
   return Output; //결과 반환
}

📝 정점셰이더

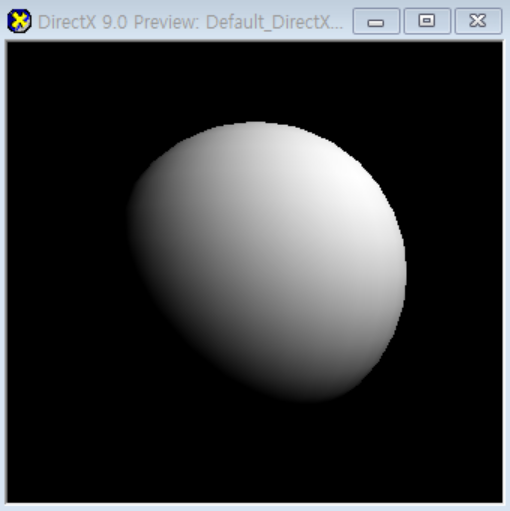
정점셰이더가 난반사광을 계산해줬으니 픽실셰이더는 그 값을 가져다 출력하면된다.

struct PS_INPUT{
   float3 mDiffuse : TEXCOORD1;
};

float4 ps_main(PS_INPUT Input) : COLOR
{   
   float3 diffuse = saturate(Input.mDiffuse); //난반사광의 범위를 -1~1에서 0~1로 바꿔준다.
   return float4(diffuse, 1); 
}

◾ 정반사광 `Specular Light`

한 방향으로만 반사되는 빛
입사각과 출사각이 같다.
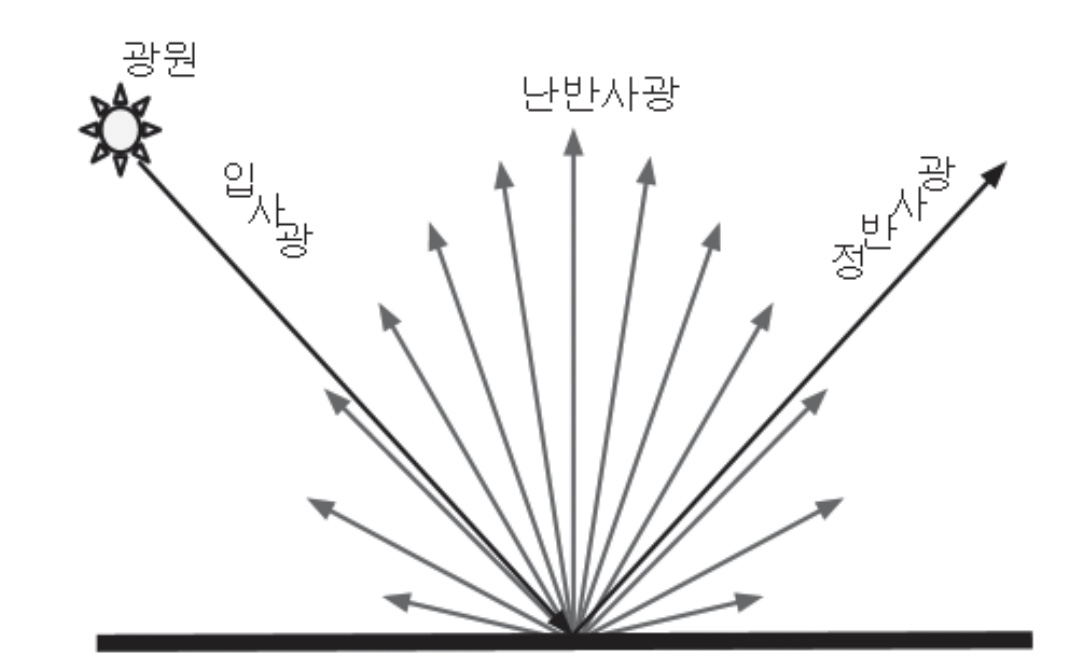
빛이 반사되는 방향에서 물체를 바라봐야만 효과를 볼 수 있다.

☑️퐁 모델 Phong

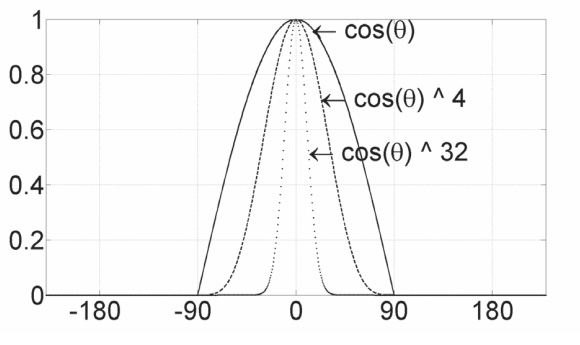
반사광과 카메라벡터가 이루는 각도의 코사인 값을 구하고, 그 결과를 여러번 거듭제곱한다.

정반사광의 좁은 폭을 재현하기 위해 거듭제곱하여 코사인값이 빠르게 줄어들도록 한다.

표면의 재질에 따라 제곱 횟수를 다르게 한다.

📝 기초설정

위에서 작성한 난반사광 셰이더에 정반사광 조명코드를 추가하여 두 광이 합쳐진 최공 결과를 만든다.
카메라 벡터를 전역변수로 만들고 이름을 gWorldCameraPosition으로 수정한다. ViewPosition 변수 시맨틱을 대입한다.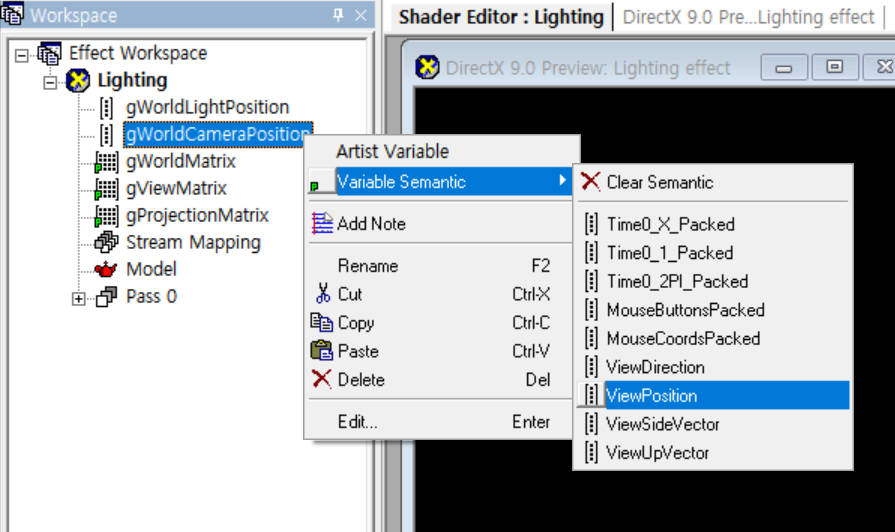

📝 정점셰이더

1. 전역변수와 입출력데이터

전역변수에 카메라 벡터를 추가하고, 입력데이터는 변화 없다.
정반사광을 구하기 위해 거듭제곱을 하고난 후, 픽셀셰이더에서 보간을 해야되기 때문에 이 계산에 필요한 두 방향벡터인 V, R을 구해 픽셀셰이더에 전달해줘야한다.

float4x4 gWorldMatrix;
float4x4 gViewMatrix;
float4x4 gProjectionMatrix;

float4 gWorldLightPosition;
float4 gWorldCameraPosition; //카메라 벡터

struct VS_INPUT{
   float4 mPosition : POSITION;
   float3 mNormal : NORMAL;
};

struct VS_OUTPUT{
   float4 mPosition : POSITION;
   float3 mDiffuse : TEXCOORD1;
   float3 mViewDir : TEXCOORD2; //V - 카메라벡터
   float3 mReflection : TEXCOORD3; //R - 반사광
};

2. 함수

카메라 벡터를 구하는 코드, 정반사광의 방향벡터를 구하는 코드를 추가한다.

VS_OUTPUT vs_main(VS_INPUT Input){
   VS_OUTPUT Output;
   
   Output.mPosition = mul(Input.mPosition, gWorldMatrix);
   
   float3 lightDir = Output.mPosition.xyz - gWorldLightPosition.xyz;
   lightDir = normalize(lightDir);
   
   //카메라 벡터
   float3 viewDir = normalize(Output.mPosition.xyz - gWorldCameraPosition.xyz);
   Output.mViewDir = viewDir;
   
   Output.mPosition = mul(Output.mPosition, gViewMatrix);
   Output.mPosition = mul(Output.mPosition, gProjectionMatrix);
   
   float3 worldNormal = mul(Input.mNormal, (float3x3)gWorldMatrix);
   worldNormal = normalize(worldNormal);
   
   
   Output.mDiffuse = dot(-lightDir, worldNormal);
   
   //입사광의 방향벡터, 반사면의 법선을 reflect함수에 전달하여 반사벡터를 구한다.
   Output.mReflection = reflect(lightDir, worldNormal);
   
   return Output;
}

📝 픽셀셰이더

1. 입력데이터

struct PS_INPUT{
   float3 mDiffuse : TEXCOORD1;
   float3 mViewDir : TEXCOORD2; //카메라벡터
   float3 mReflection : TEXCOORD3; //반사광
};

2. 함수

float4 ps_main(PS_INPUT Input) : COLOR
{   
   float3 diffuse = saturate(Input.mDiffuse);
   
   //카메라벡터와 반사광의 정규화 (정점셰이더 이미 했지만 보간기를 거치는 동안 그 값이 흐트러질 수 있기 때문)
   float3 reflection = normalize(Input.mReflection);
   float3 viewDir = normalize(Input.mViewDir);
   
   //정반사광 구하기
   float3 specular = 0;
   if(diffuse.x > 0){ //난반사광이 존재하지 않는 표면에는 이미 빛이 닿지 않아 정반사광도 존재할 수 없다.
      specular = saturate(dot(reflection, -viewDir)); // -viewDir를 사용한다.
      specular = pow(specular, 20.0f); //거듭제곱 (수가 높을수록 정반사광의 범위가 좁아짐)
   }
   
   float3 ambient = float3(0.1f, 0.1f, 0.1f); //임의로 정의해준 간접광
   
   return float4(ambient + diffuse + specular, 1);
}

jungizz_

( •̀ .̫ •́ )✧

이전 포스트

[셰이더 프로그래밍 입문] Part1 | 셰이더 프로그래밍 기초 (Chapter1~2)

다음 포스트

[셰이더 프로그래밍 입문] Part1 | 셰이더 프로그래밍 기초 (Chapter3~4)

Shader Programming

Chapter 3 | 텍스처매핑

🆕 HLSL

◾ 텍스처매핑과 UV좌표

📝 기초설정

📝 정점셰이더 코드

📝 픽셀셰이더 코드

❗픽셀셰이더의 입력데이터 = 정점셰이더의 출력데이터

☑️ 정점버퍼에서 올바른 UV좌표 값으로 불러오기

➕ Swizzle

◾DirectX 프레임워크

Chapter 4 | 기초적인 조명셰이더

🆕 HLSL

❗간접광(전역조명모델)과 직접광(지역조명모델) 중에서 직접광만 다뤄본다.

◾ 빛의 구성 요소

◾ 난반사광 `diffuse Light`

☑️ 람베르트 모델 `Lambert`

📝 기초설정

📝 정점셰이더

❗ 동일한 계산을 픽셀셰이더와 정점셰이더 둘 다에서 할 수 있다면 정점셰이더에서 하는 것이 성능상 유리하다.

📝 정점셰이더

◾ 정반사광 `Specular Light`

☑️퐁 모델 `Phong`

📝 기초설정

📝 정점셰이더

📝 픽셀셰이더

[셰이더 프로그래밍 입문] Part1 | 셰이더 프로그래밍 기초 (Chapter1~2)

[셰이더 프로그래밍 입문] Part2 | 셰이더 프로그래밍 응용 (Chapter5~6)

0개의 댓글

[셰이더 프로그래밍 입문] Part1 | 셰이더 프로그래밍 기초 (Chapter3~4)

Shader Programming

Chapter 3 | 텍스처매핑

🆕 HLSL

◾ 텍스처매핑과 UV좌표

📝 기초설정

📝 정점셰이더 코드

📝 픽셀셰이더 코드

❗픽셀셰이더의 입력데이터 = 정점셰이더의 출력데이터

☑️ 정점버퍼에서 올바른 UV좌표 값으로 불러오기

➕ Swizzle

◾DirectX 프레임워크

Chapter 4 | 기초적인 조명셰이더

🆕 HLSL

❗간접광(전역조명모델)과 직접광(지역조명모델) 중에서 직접광만 다뤄본다.

◾ 빛의 구성 요소

◾ 난반사광 diffuse Light

☑️ 람베르트 모델 Lambert

📝 기초설정

📝 정점셰이더

❗ 동일한 계산을 픽셀셰이더와 정점셰이더 둘 다에서 할 수 있다면 정점셰이더에서 하는 것이 성능상 유리하다.

📝 정점셰이더

◾ 정반사광 Specular Light

☑️퐁 모델 Phong

📝 기초설정

📝 정점셰이더

📝 픽셀셰이더

[셰이더 프로그래밍 입문] Part1 | 셰이더 프로그래밍 기초 (Chapter1~2)

[셰이더 프로그래밍 입문] Part2 | 셰이더 프로그래밍 응용 (Chapter5~6)

0개의 댓글

◾ 난반사광 `diffuse Light`

☑️ 람베르트 모델 `Lambert`

◾ 정반사광 `Specular Light`

☑️퐁 모델 `Phong`