[컴퓨터 비젼] CV-03 Edge

jungizz_·2023년 10월 18일

Computer Vision

목록 보기

3/8

Edge detection

목표: 함축적인 정보, 정보를 알기 쉬워짐

Edge

surface normal discontinuity: 노멀 벡터가 급격히 변해서
depth discontinuity: 급격히 차이나는 깊이 (카메라와의 거리)
surface color discontinuity: 색이 달라서
illumination discontinuity: 빛의 정도 (ex-그림자)
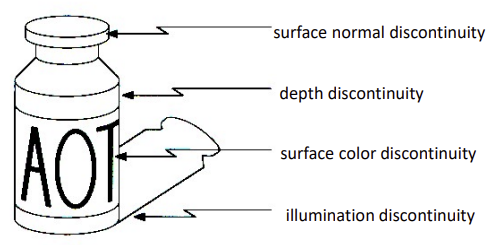
공통적으로, 보통 색/밝기 가 달라서 체크되는 edge
edge는 밝기가 급격히 변하는 부분이다.
-> 이미지 intensity 함수에서 rapid change 부분
급격히 변하는 곳을 알기 위해 미분 -> extrema(극값)가 edge일 가능성이 높다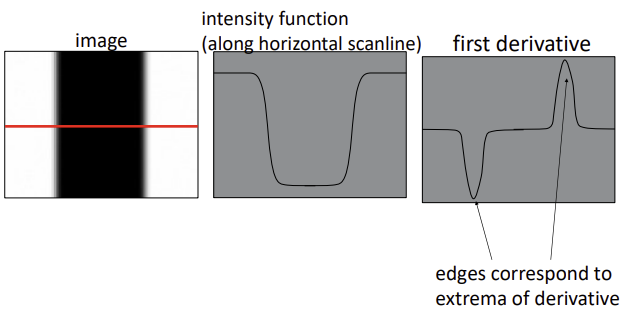(가로축은 gradient 방향, edge의 수직인 방향)

Effects of noise

노이즈가 있는 상태에서 미분하면, 밝기 차이로 인해 노이즈의 미분값도 크게 나와 edge와 헷갈림
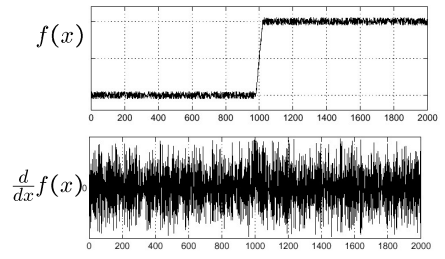
노이즈를 없애기 위해 low-pass filter 적용

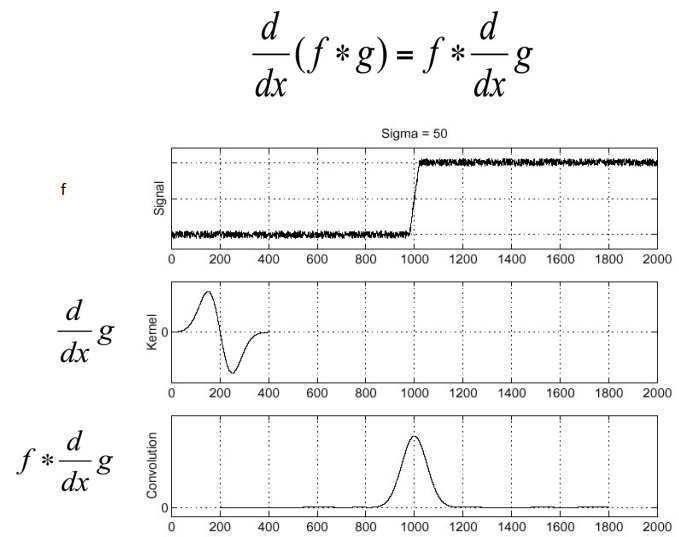
Gaussian filter 적용한 뒤 미분
-> 극값에 해당하는 곳이 edge

Gaussian을 미분한 뒤, f와 Convolution해도 결과는 비슷 (linear하기 때문)

Gaussian을 두 번 미분한 뒤(Laplacian) 이미지와 Convolution (Laplacian of Gaussian)(= (=Gaussian filter를 적용한 이미지를 두 번 미분)
-> zero-crossing하는 곳이 edge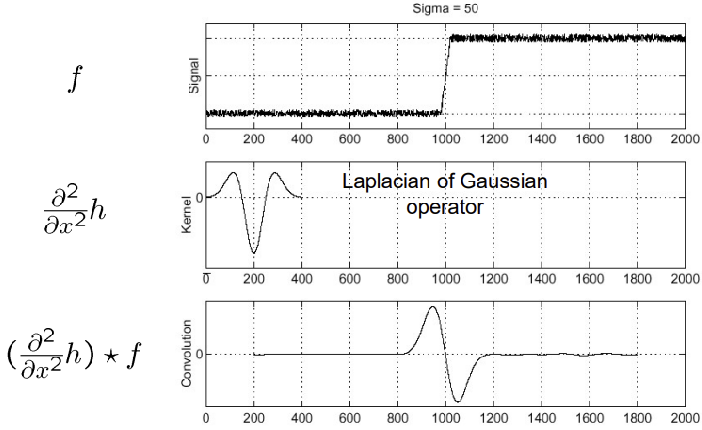

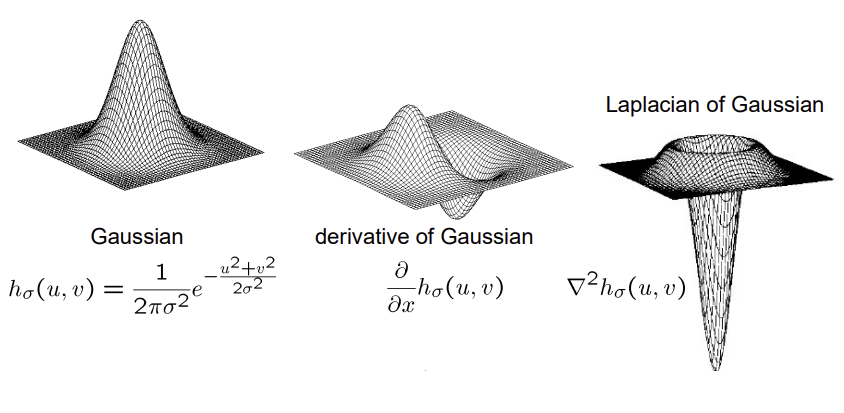
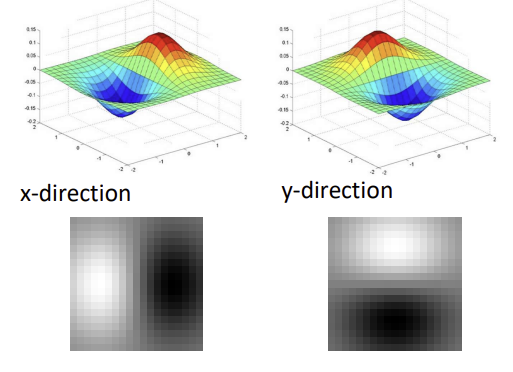
2D edge detection filters

Gaussian 한 번 미분 / Laplacian of Gaussian

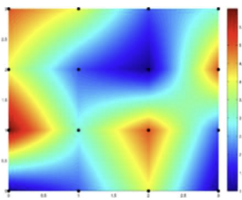
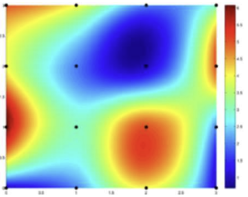
Gaussian의 sigma

σ가 클수록 범위가 커짐 (블러가 많이 됨)
σ를 픽셀 단위로 생각할 때, 아래 그림을 보면 Edge는 σ정도에 따라 다르게 나오며 값이 낮을 수록 미세한 값까지 나타난다는 것을 알 수 있다
noise(edge로 보지 않을 것)와 signal(edge로 볼 것)의 정도를 정하는 역할!

Gradient

x축 미분, y축 미분 (벡터로 합침)
Gradient magnitude(길이): 밝아지는 정도
(클수록 급격히 밝아짐 -> edge)
-> 근데 두꺼운 edge로 나타나고 이어진 edge인지 판별이 어려움
Gradient direction(방향): 밝아지는 방향

두꺼운 edge의 이유
1. 원래 사진이 뿌옇다
2. Edge가 애매
3. Gaussian

Edge detector

edge가 연결된 구체적 범위 제안
두꺼운 edge 중 실제 이미지의 선과 비슷한 한 가닥 edge를 찾아냄 (Localization)

Canny edge detector

Gaussian 노이즈에 강한 edge detector
현재까지도 가장 많이 사용되는 edge detector
5단계로 구성

Gaussian 미분한 걸로 filtering
Gradient 계산 (x, y방향으로 미분된 Gaussian Convolution)
-> edge의 magnitude와 direction 얻음
-> 두꺼운 edge
- Gaussian은 separable한 filter
  - x축으로 filtering + y축 filtering = box convolution
  - 장점⭐: kernel의 크기가 mxm이면 이미지크기xmxm의 complexity인데, separable하게 계산하면 이미지크기xmx2가 되므로 complexity가 줄어듦
  - 위에서 Gaussian 미분하고 filtering하는 것보다, seperable하게 filtering한 뒤 미분하는게 더 빠름
Non-maximum supperssion
- gradient 방향을 고려해서 1pixel의 edge 구하기
- 두꺼운 edge에서 진짜 선을 찾아내기 (Maximum이 아닌거는 눌러버린다)
  -> 하나의 edge가 여러 개의 픽셀로 표현되는 현상 없애기
- 두꺼운 Edge에서 Edge방향의 수직방향은 선이 두껍게 퍼저가나는 방향 즉, Gradient의 방향을 나타낸다.
  - Edge의 수직 방향 = Gradient의 방향
  - Gradient의 수직 방향 = Edge 방향
- Gradient 방향에 위치한 픽셀들을 조사하여 Gradient의 크기가 local maximum인 픽셀만을 edge로 설정하고 나머지는 0으로 설정
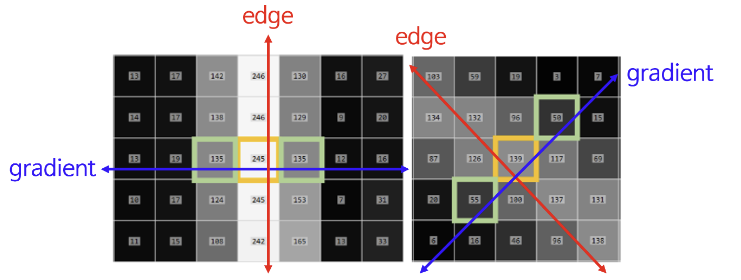
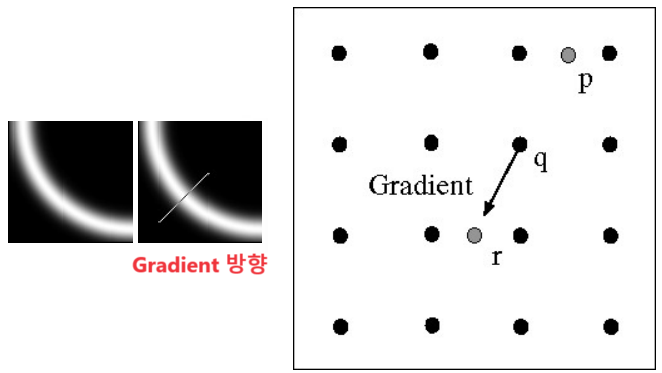
- Edge와 Gradient가 직교이고, Gradient방향으로 NMS를 적용하기 때문에 단일 edge를 선택할 수 있는 것
- Magnitude가 남아있는 상태
- 보간????????????????????이 어디에..

gradient방향에서는 maximum만 찾고(연결X), edge의 방향으로 연결 -> maximum들은 edge의 방향대로 모여있음

Edge linking
- NMS 과정에서 Edge가 끊어지는 것 보완
- NMS에서 선정된 Maximum pixel에서 edge 방향을 찾고(수직), 다음 edge pixel(r 또는 s)을 추측한다(NMS).
  (큰 값을 찾고 따라가는 방식을 반복)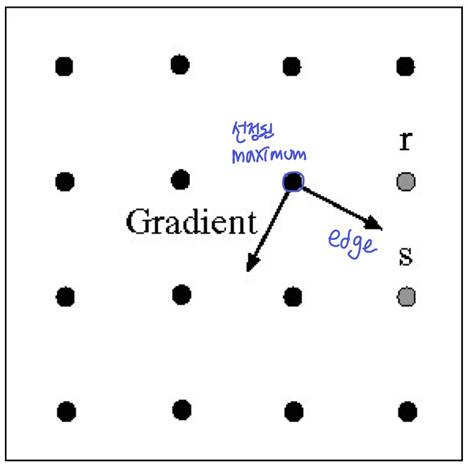

4번의 gradient의 방향으로 움직이면서 3번의 NMS 진행 -> 한 pixel의 선을 그릴 수 있게됨

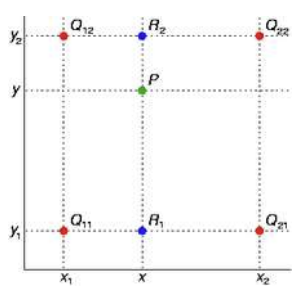
+) Bilinear Interpolation

점 P의 밝기 찾기

점 R값 찾기
- R1 = (1-x)Q11 + xQ21
- R1 = (1-x)Q12 + xQ22
점 P값 찾기
- P = yR1 + (1-y)R2

x, y 순서 상관 없음

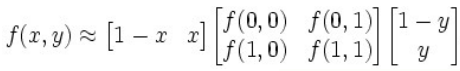
+) Interpolation options

각 이미지의 점에 color가 주어진 경우 Interpolation 방법들
nearest(neighbor)
- 가장 가까운 점의 값 가져오기
bilinear
- 점과 점에 선을 그어서 비율에 따라 구하기 (2x2= 4)
bicubic
- 점 4개로 3차함수를 만들어서 구하기 (4x4=16)
- 3차 함수를 그리면서 원래 값보다 크거나 작은 값이 나타나는 Overshooting 문제가 edge 근처에 생길 수 있다.

Hysteresis thresholding
- NMS 후, gradient magnitude가 남아있는 상태이고,
- Edge인지 아닌지 판별하기 위해 특정 값 이상만 살리도록 함(thresholding값을 정하고 못넘으면 0으로) -> 그 중 Hysteresis thresholding 사용
- NMS 후, 3종류로 구분
1. 너무 작아서 Edge 가능성 작은 픽셀 -> 삭제
2. 너무 커서 Edge 가능성이 큰 픽셀 -> 유지
3. 중간값의 픽셀-> 고민
  - 3번과 2번이 연결되어있다면, 3번을 살릴 가능성이 크다.
- gradient value의 maximum 값을 확인하여 시작 edge에서는 높은 threshold, 이어지는 edge에는 낮은 threshold
- 고민되는 edge가 확실한 edge와 붙어있다면 살리고, 붙어있지 못한 고민되는 edge는 삭제됨
  - 선택된 edge에서 다음 edge픽셀을 찾는 법: gradient의 방향을 알고 있으므로 -> edge방향 알아냄 -> edge방향으로 갔을 때 근처에 있는 한 점 중 dge로 선택된 픽셀또는 고민되는 edge가 있다면 그 방향으로 이어감 (없다면 멈춤)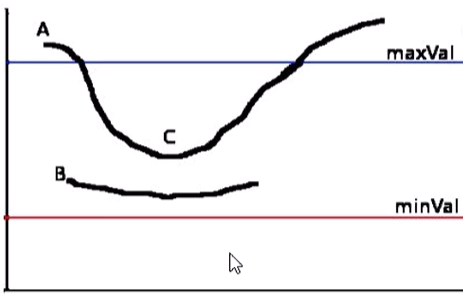(위 이미지에서 C는 살고, B는 죽음)

algorithm

Effect of σ (Gaussian Kernel spread/size) ⭐

위에도 나온 이야기이지만 Gaussian의 σ값은 중요하다
σ가 크면: detect large scale edges (대략적인 edge)
σ가 작으면: detects fine features (세부적인 edge까지)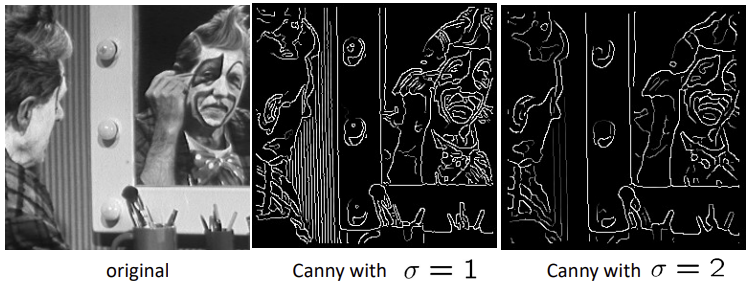

Lines

edge는 line이 아니다
직선을 알게되면 방정식으로 나타내는 등 사용 방법이 늘어나므로 line을 찾는 것은 중요

representation lines

y = mx + b
- y축과 평행한 직선을 표현할 수X (m이 무한대)
ax + by + c = 0
- homogeneous로 나타내면
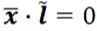
- a, b, c ( $\tilde{l}$ )에 의해 표현된 Line
- 하나의 직선을 나타낼 수 있는 a, b, c 조합이 많다. 3개의 자유도는 많다. (상수배해도 동일한 직선이므로)
  (a, b, c가 homogenouse 하다)
normalization:
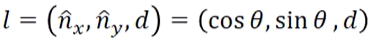
- a, b의 길이를 1로 만든 n과 그때의 d로 line 표현
- 자유도는 2개(θ, d)
  -> unique하고 complete (한 직선에 대한 한 쌍의 (θ, d)만 나오고, 모든 line을 표현 가능)

(θ, d)로 표현한 line

원점에서 θ만큼 꺾이고 거리가 d인 벡터의 수직인 직선
-> xcosθ + ysinθ = d를 만족하는 직선

Finding lines in an image

한 밝은 점 주변에서 자신과 동일한 기울기를 가지는 점과 직선이라고 인식 -> 더 이상 주변에 동일한 기울기의 점이 없을 때까지 반복
이미지 상에 가능한 모든 위치/방향에서의 line을 그리고 일치하는 line을 찾기 -> 힘드므로 Hough transform이라는 방법으로 직선을 찾는다.

Hough transform

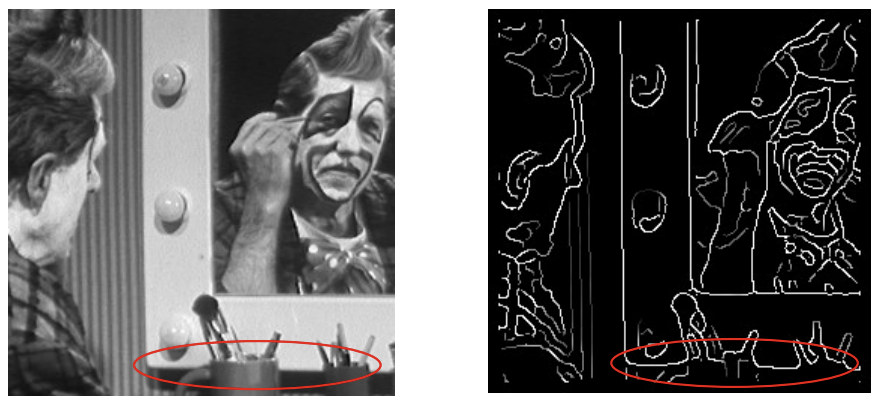
노란 선들과 대각선의 교점 -> 어떤 line의 점일까?
해당 점은 노란 선 2개와 대각선 (총 3개)의 라인에 해당하는 점이다. -> 점마다 해당할 수 있는 Line이 한정적이므로, 점에 해당할 수 있는 후보 line들 중 해당하는 line에 투표
모든 점에 대해 투표를 반복한 뒤, 가장 많은 투표를 받은 line이 line이다.

Hough space

θ와 d가 세로, 가로축인 table
픽셀들이 자신이 해당하는 line의 θ와 d으로 table에 해당하는 점을 투표
hough space에서 한 점 -> 실제 이미지에서의 한 점
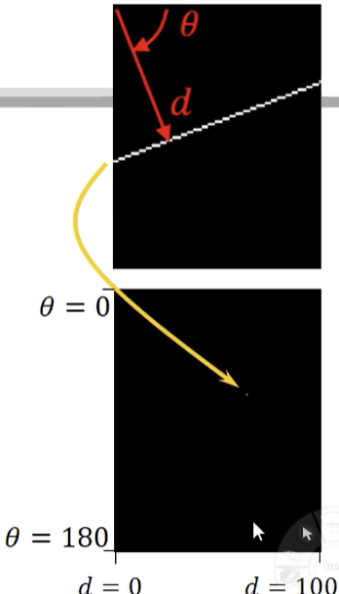
이미지의 한 점을 지나는 무수히 많은 직선들을 hough space에 나타내면 아래처럼 나타난다
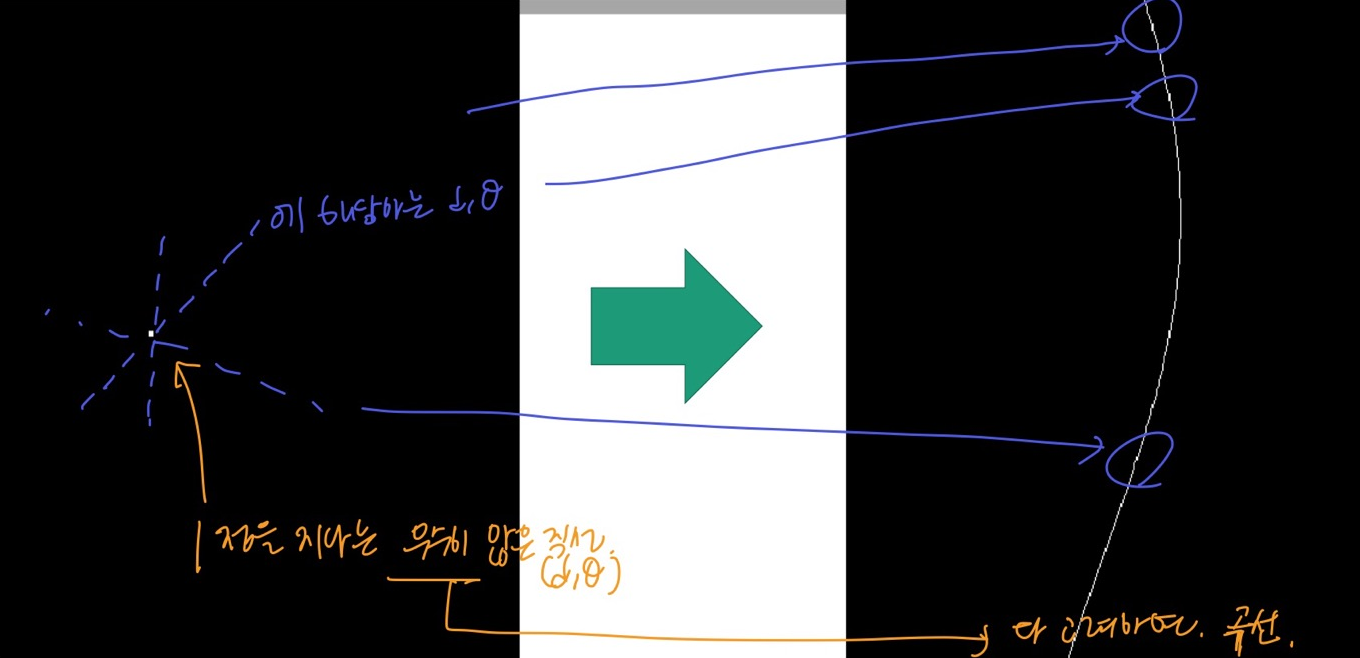
- 각 직선은 hough space에 점을 찍고, 무수히 많은 직선들은 hough space에 무수히 많은 점을 찍어 곡선을 만든다
점이 두 개라면?
- hough space에서 두 곡선이 생기고 두 곡선의 교점이 생긴다. (2표를 받은 점)
- hough space에서 만다는 점은 두 점을 지나는 직선의 점이다.

algorithm

example

hough space에서 파란 부분은 vote 0, 붉을수록 vote 수가 많다 (edge에 해당하는 점)
붉은 point의 θ와 d값으로 image 상에서의 line의 방정식을 찾을 수 있다
(교수님이 가로선과 세로선을 반대로 말씀하신거 아닌가)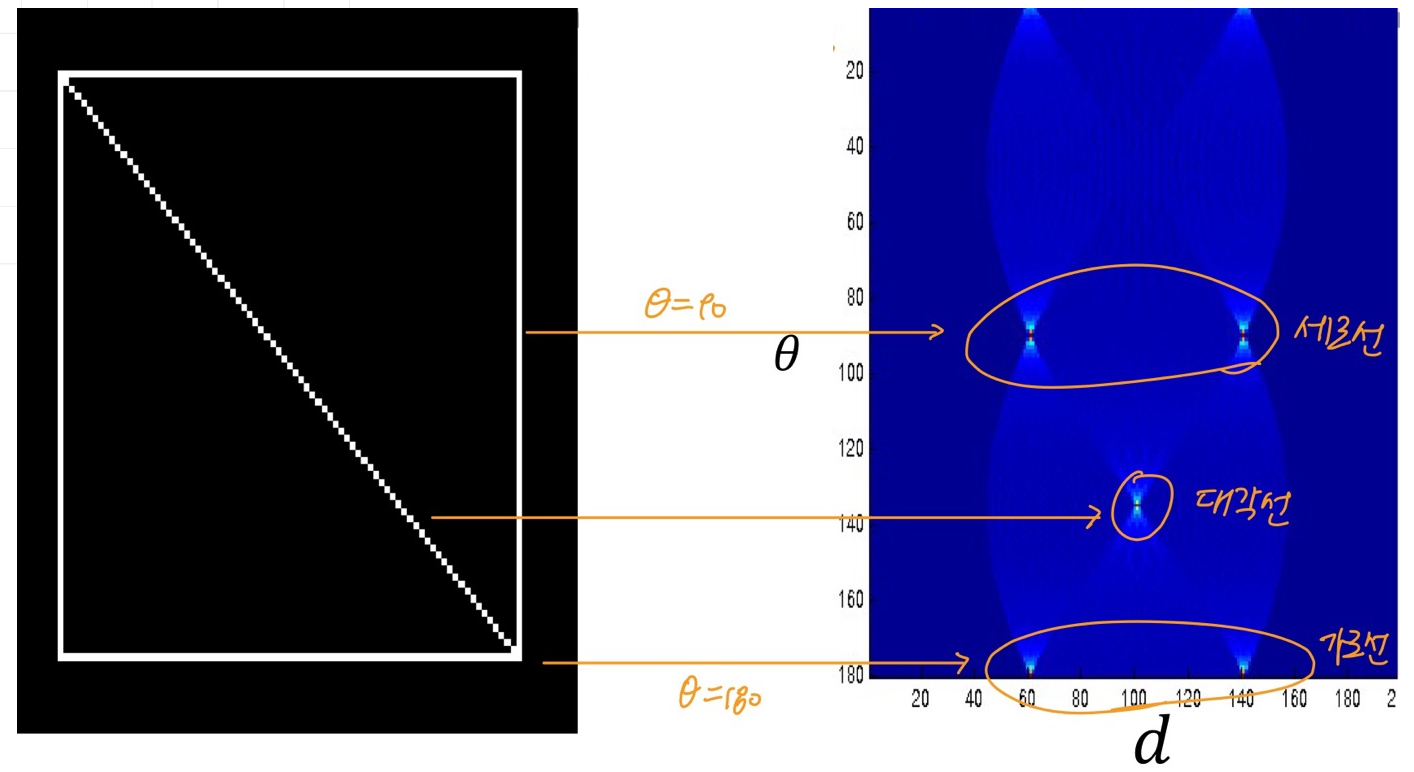

Extensions

image gradient 사용
- Edge의 방향은 gradient 방향의 수직이므로, gradient 방향을 사용하기도 함
- edge의 방향을 보고, gradient 방향을 찾고 -> 이에 해당하는 θ에 투표 (근데 잘 안됨)
gradient magnitude가 큰 애들은 더 많이 투표
- 확실히 edge인 것 같은 선에게 가중치를 더 많이
(θ, d)의 resolution 바꾸기
- 지금까지는 1도 단위로 한 θ를 사용했는데,
- resolution을 높여서 더 작은 단위의 θ를 사용하면 더 세밀한 범위로 line을 찾을 수 있음
  (대신 line 당 vote 수가 줄어듦)
  - 굉장히 비슷한 기울기인데 다른 line으로 처리할 수도 있음
- 세밀한 edge가 아닌 대강 찾고싶으면 resolution을 낮게
  - 비슷한 기울기인 다른 line을 같은 line으로 처리
- (pixel 단위기 때문에 한 픽셀 어긋나면 완전 어긋나보일 수 있으므로 정밀한 조절이 필요)

Circle Hough Transform

원의 방정식 (원의 중심 a, b와 반지름 r -> 무조건 자유도 3개)
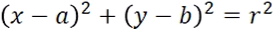
자유도가 3개라서 hough space의 table로 나타내기 어려움 (3차원이니까)
이미지의 한 점에서, 이 점을 포함하는 모든 원을 나타내기 위해 table에 원의 중심을 나타냄
여러 점을 circle hough space에 나타내면, 여러 점을 한번에 지나는 원의 중점을 찾을 수 있다.
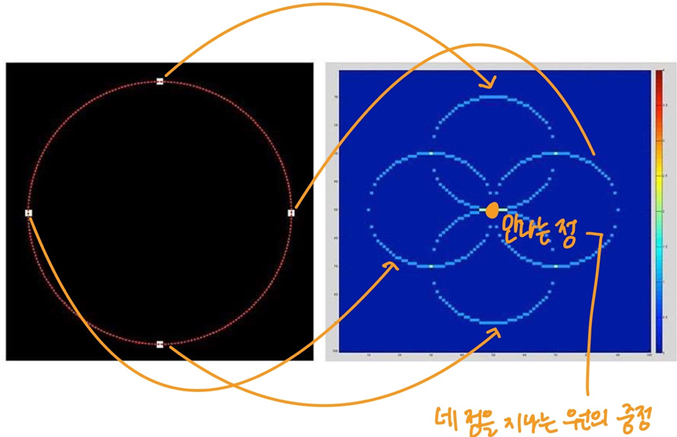
반지름은 z축으로 나타나며 뒤집힌 원뿔 형태로 보인다
위에서 circle hough transform의 교점 -> 투표를 가장 많이 받은 곳이 네 점을 지나는 원의 중점이고, 이때의 반지름은 z축으로의 값이라는 것