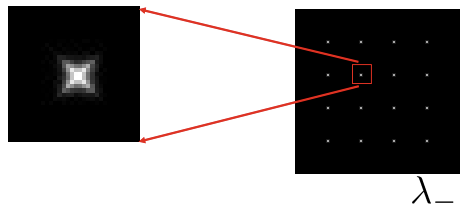
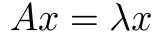how to combine image
- 두 이미지의 같은 부분을 찾기 위해 흔하게 나타나지 않는 부분, 중요한 부분(특징점; features)을 살펴봄 -> extract features

- 왼쪽 그림의 feature가 오른쪽 그림의 어떤 점에 해당하는지 -> match features

- homography로 이미지 합치기 -> align images

Features
- 뭘 하고싶으냐에 따라서 달라질 수 있음
ex) 아래 이미지를 해골로 보느냐(전반적인 윤곽, 밝기 변화를 중요시), 거울 사람으로 보느냐(내용을 중요시)
-> 특징적인 것을 설명할 때 여러개가 나올 수 있다
purpose
- matching의 목적
- 두 이미지의 특정 영역이 같은지 확인
- 이미지 전체를 보고 확인하거나 작은 부분을 많이 확인하거나
-> 우리는 작은 부분을 많이 확인할 것
Global features
- 이미지 2장 중 하나의 불투명도 조절해서 겹쳐서 전체적으로 비교
Invariant local features
- 이미지 전체가 아닌 지역적으로 확인
- 왼쪽 이미지의 특정 부분이 오른쪽 이미지의 어느 부분인지 찾고, 상당수가 일관성을 갖게 되면 같다고 판단
- 각 블록 속의 이미지의 다른 점?
-> 크기, 위치, 방향, 밝기, 노출, ... - 위의 요소들이 다른 이미지지만, 두 이미지에서 동시에 중요하다고 판단되는 부분이 있으면 invariant(불변) local feature이라고 한다.
- Geometric invariance
- translation, rotation, scale
- 크기, 위치, 방향이 달라도 중요한 점을 동시에 찾아낼 수 있으면 geometrically하게 invariant하다.
- Photometric invariance
- brightness, exposure, ...
- 밝기가 달라도 찾을 수 있으면 photometric하게 invariant하다
Advantages of local features
- 이미지 전체가 아닌 지역적으로 확인하는 것의 장점
- Locality
- features are local, so robust to occlusion and clutter
- 전체적으로 달라보여도(장애물, 일부 가려짐) 지역적으로는 feature를 찾을 수 있다
- Distinctiveness (특수성)
- can differentiate a large database of objects
- 데이터베이스 내에서 객체를 구별하는데 효과적
- ex) 사람 얼굴의 눈, 코, 입 -> 눈코입 가지면 사람이더라
- Quantity
- hundreds or thousands in a single image
- 매칭할게 많아서 pair가 많아져 안정적
- Efficiency
- real-time performance achievable
- 작은 부분을 비교하므로 효율적 (실시간 처리에 굳)
- Generality
- exploit different types of features in different situations
used for
- Image alignment
- Image alignment를 inverse하면 카메라 위치를 찾을 수 있음 -> AR, 3D reconstruction
- Motion tracking
- 데이터들을 보고 Object recognition
- Indexing and database retrieval
- Robot navigation
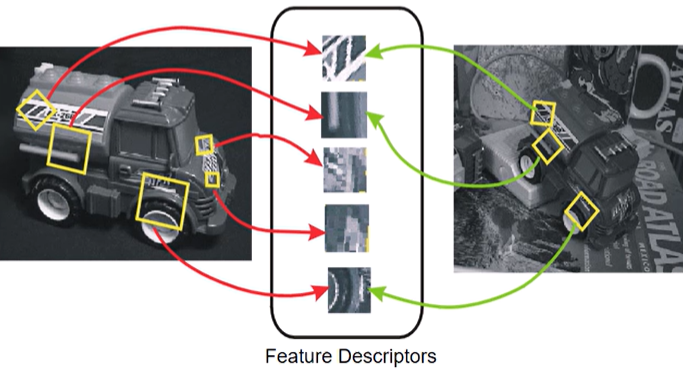
1. Feature Detection (Finding feature points)
- 작은 window로 local measures of uniqueness
- window를 움직였을 때, 변화가 나타나는 부분이 unique/unusal한 부분이다 -> Corner
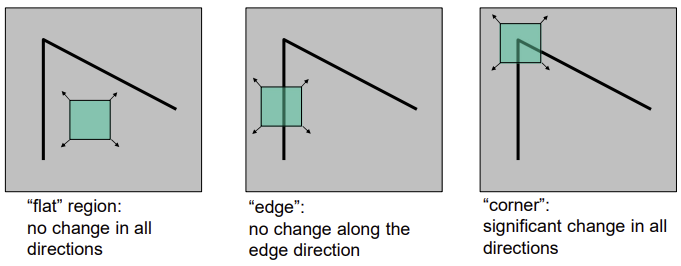
Corner detection: SSD error E(u, v)
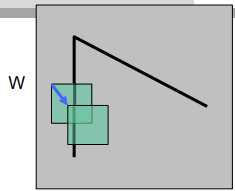
- window
W(x, y) - window 이동
u, v - window를 이동하면 window안의 픽셀이 얼마나 변하는지 확인
-> 움직인 window와 원본 window를 픽셀별로 빼고 각 x, y에 대해 제곱해서 더하는 SSD (sum of squared differences)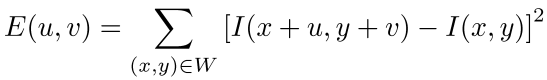
E(u, v): u, v만큼 window를 움직였을 때 픽셀별 차이 값 -> 차이값(SSD)이 크면 다르다 -> x, y 부분은 unique하다- 제곱을 하는 이유는 음수가 나오는 것을 방지하고, 절댓값 함수는 0에서 미분이 안되므로 사용하지 않음
- 테일러 급수를 사용해서 식을 단순화할 수 있다
Taylor Series
테일러 급수 (u, v가 작을 때, 테일러 급수의 첫번쨰 항으로만의 approximation은 ㄱㅊ)
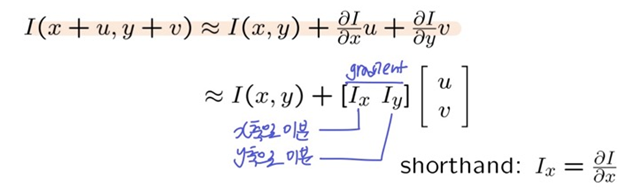
- 테일러 급수를 적용하여 I(x, y)가 삭제되고, u, v가 작을 때만 사용할 수 있는 approximation값을 만듦 (정확한 값은 아님)
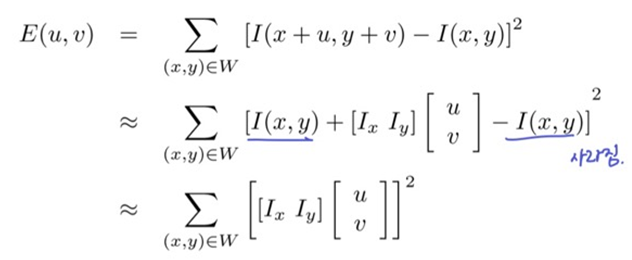
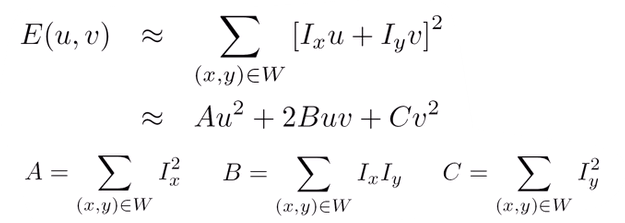
- 행렬식
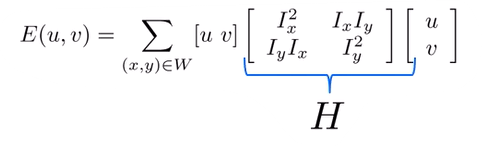
- 임의의 u, v에 대한 이미지 성질이(얼마나 unique)한지 H(Harris Matrix)에 나타난다
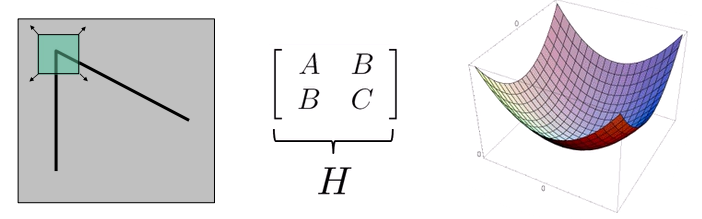
Harris Matrix
- 2차식인 H의 최소값을 구하는게 목표 (아래에 H를 통해 그린 그래프)
- 가장 이상적인 H의 형태 (Quadratic form; 2차식)
- u, v에 대해서 모든 값이 전부 커짐
- 가장 우측 그림의 가로축은 u, 세로축은 v, 높이는 SSD error
- u=0, v=0인 가운데에서는 0의 값을 가진다 -> window를 움직이지 않았을 때 변화X
- Horizontal Edge
- x축으로 미분했을 때 변화X
Ix=0->A=0,B=0 - v축으로만 변화
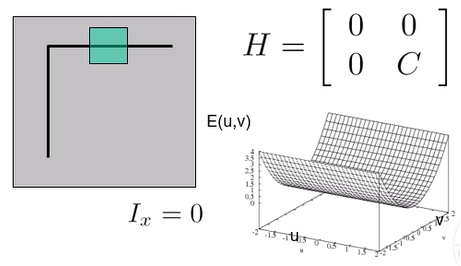
- x축으로 미분했을 때 변화X
- Vertical Edge
- y축으로 미분했을 때 변화X
Iy=0->C=0,B=0 - u축으로만 변화
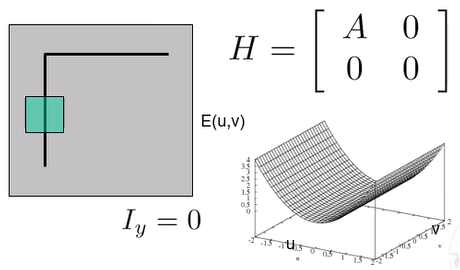
- y축으로 미분했을 때 변화X
- 이 내용을 일반식으로 나타내기 위해 Eigen analysis
1. Eigen analysis
Eigen
- 벡터
x에 선형변환A를 취했을 때, 방향은 변하지 않고 크기만 변한 경우- 이때의 방향을 나타내는 단위벡터
x가 eigen vector(고유벡터)- 이때의 크기를 나타내는 값
λ가 eigen value(고유값)- eigen value는 2개 (
λmin,λmax)- Eigen analysis로 행렬이 나타내는 성질/방향성을 찾는다
Visualize H as an ellipse
- 위처럼 Harris matrix를 구했다면 H의 eigenvalue와 eigenvector를 정의하여 타원 방정식을 계산할 수 있음
- 이때 eigenvalue의 최소값인
λmin을 구해 가장 천천히 변하는 방향을 알아낼 수 있따 - E값이 상수가 되는 경우의 궤적이 타원 형태
- 변하는 정도에 따라 타원의 장/단축이 결정되고, 극단적으로 한 축 무한적으로 길어지는 경우는 Horizontal/Vertical edge인 것
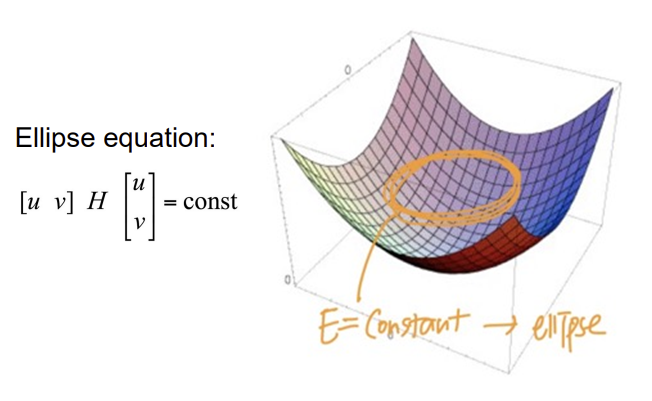
- 타원 축의 방향은 H의 eigen vector, 장/단축의 반지름은 H의 eigen value
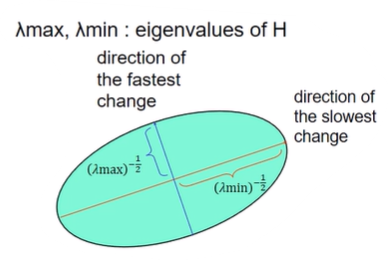
ex) eigen value가 작으면 축이 길다 (역수니까) -> 축이 길다는 것은 그 방향으로 움직여도 변화가 적다 -> SSD가 작다 (그래프에서 변화량이 작으면 높이 변화가 거의 없음 -> 타원으로 그렸을 때 축이 길다) - eigen analysis로 장/단축을 확인하고 방향에 따른 SSD가 얼마나 빨리 변할지를 찾아낼 수 있다
eigenvalue / eigenvector of H
- eigen value가 큰 방향이 eigen vector이고, 그 방향으로의 변화가 크다(=SSD가 크다)
- 이때 변화 정도는 해당 eigen value
λ+: 큰 eigenvalue; 조금만 움직여도 변화가 큰x+: 큰 eigenvalue에 해당하는 방향 (eigen vector)λ-: 작은 eigenvaluex-: 작은 eigenvalue에 해당하는 방향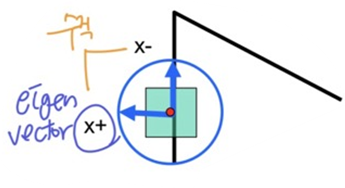
x+와x-는 수직- unique하다는 것은 eigenvalue가 크거나
λ+eigenvalue가 작은 애들λ-중에서 크거나 λ+는 edge만 나오고,λ-는 corner만 나옴- 변화율이 작은
λ-방향으로 움직였을 때도 많이 변하는게 코너 (작은 것 중에서도 큰 것)- 두 eigenvalue가 크면 (=threshold를 넘으면) 코너인데, 두 eigenvalue 중 작은 것만 thereshold를 넘으면 둘 다 넘는 것이니까
λ-이 threshold보다 크다로 코너를 판단⭐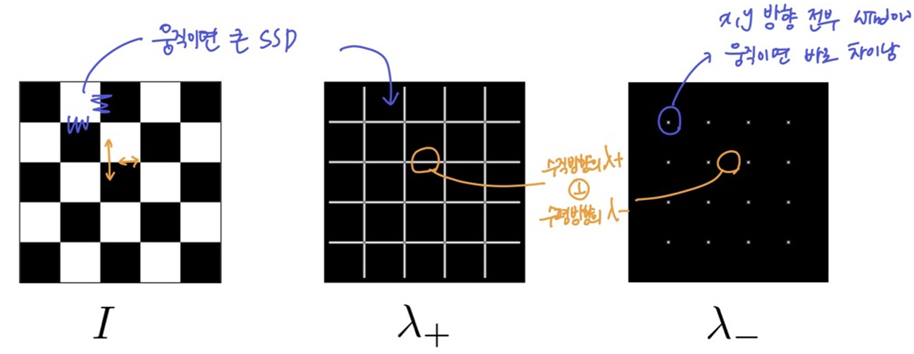
- 두 eigenvalue가 크면 (=threshold를 넘으면) 코너인데, 두 eigenvalue 중 작은 것만 thereshold를 넘으면 둘 다 넘는 것이니까
Classification and Interpreting of eigenvalues
- 수평 방향의
λ1과 수직 방향의λ2
- 수직 edge
λ1이 크고,λ2가 작다
- 수평 edge
λ2이 크고,λ1가 작다
- Flat
λ1와λ2둘 다 작다
- Corner
λ1와λ2둘 다 크다 (두 eigenvalue가 threshold를 넘으면 코너)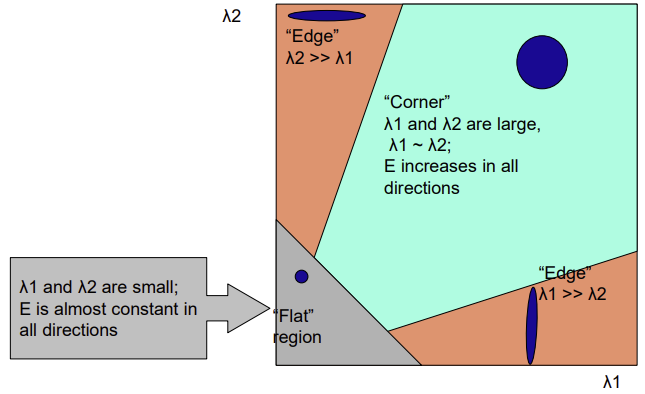
λ가 한 쪽 방향만 크면 edge일 가능성이 크고, 둘 다 크면 corner일 가능성이 높다
summary
- gradient 계산 (이미지 전체에 대해 x, y축 미분)
- 모든 픽셀에 대해 window 만들고 Harris matrix 계산 (SSD)
- H의 eigenvalues 계산 (
λ+,λ-)- points 찾기 ->
λ-가 threshold를 넘으면 corner- point들 중
λ-가 local maximum인 곳을 feature로 결정
2. Harris operator (Harris Corner Detector)
- Eigen analysis 대신 harris matrix를 활용해서 feature detection하기
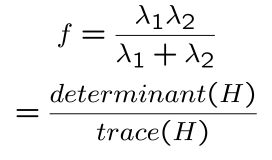
- 분모
λ1λ2는 둘 중 하나가 작으면 0에 가깝고, 둘 다 크면 크다 -> determination(H) - 분자
λ1+λ2은 전체적인 scale/balance를 맞추기 위해 -> trace(H) - 큰
f가 corner (threshold를 넘는f중 local maximum)
- 분모
- determination(H)는
λ-와 비슷하지만 비용이 적음 (no square root) - eigen value를 각각 구하는 것 보다, 합곱을 구하는게 더 쉬움 (det은 ad-bc, trace는 대각선 행렬의 합)
- 가장 자주 쓰이는 operator

Invariance properties
- 상황이 다른 두 개의 사진에서 중요한 점을 활용해서 같은 점을 찾고싶다
- 원본 이미지와 변형된 이미지를 비교할 때 detected corner가 같으면 invariant
- Harris Detector는 어떤 transformation에 invariant 할까?
Image transformations
- Geometric: Rotation, Scale
- Photometric: Intensity change, contrast
- Rotation
invariant- gradient, eigenvector는 돌아가지만, eigenvalue는 변하지 않음
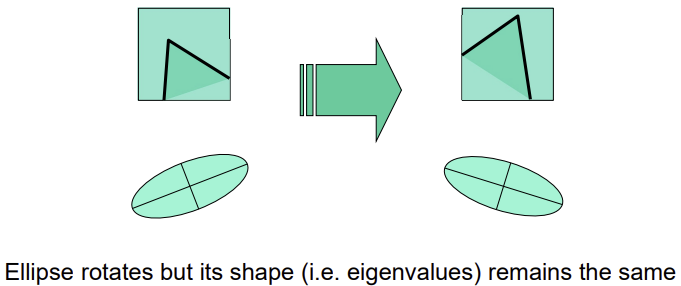
- gradient, eigenvector는 돌아가지만, eigenvalue는 변하지 않음
- Affine intensity change
partially invariant- I -> aI+b로 바뀜
- Intensity shift
b: Harris detector는 미분을 하기 때문에 bias는 영향Xinvariant - Intensity scale
a: 이미지에는 a가 곱해졌고, 미분해서 구한 H에는 a^2이 곱해짐 (gain)
-> 즉, eigenvalue에도 a^2이 곱해짐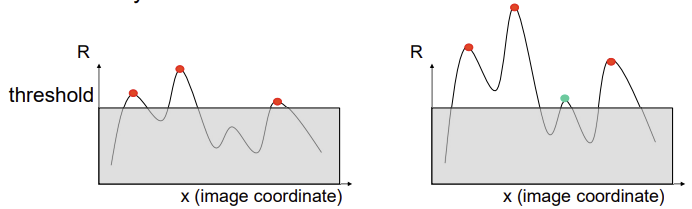
-> a에 따라 진폭이 달라져 있으므로, 동일한 threshold이지만 새로운 corner가 감지되거나, 기존 corner가 감지되지 못할 수 있음 - Intensity shift
b는 invariant하지만 intensity scalea은 부분적으로 invariant하다 (근데 거의 invariant하다..)
- Scaling
Not invariant- window 크기가 동일한 경우, 이미지가 커졌다면 corner를 인식하기 어렵고, 이미지가 작아지면 corner가 edge로 인식될 수 있다
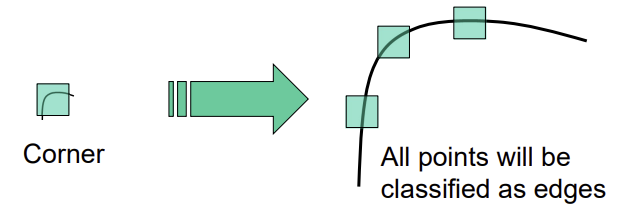
- window 크기가 동일한 경우, 이미지가 커졌다면 corner를 인식하기 어렵고, 이미지가 작아지면 corner가 edge로 인식될 수 있다
Scale invariant detection
- Scale invariant한 harris detection
ex) 이미지가 커져서 이미지를 줄여가기 (또는 window 크기를 키움)
- 이미지가 커지면 그만큼 디테일한 부분이 잘 보이고, 새로운 feature들이 인식되니까 -> 이미지를 줄여서 확인한다
- 가장 우측 그림은 이미지가 너무 작아져서 뭉개졌기 때문에 f값이 아주 작아짐
- 중앙의 이미지 크기 (또는 window 사이즈)에서 f값이 가장 크기 때문에 가장 corner처럼 보임
- 크기가 다른 이미지를 비교할 때, 각 이미지에 위와 같은 과정을 거쳐서 가장 높은 responce(f값)이 나오는 곳을 찾아두고, 그 부분을 비교
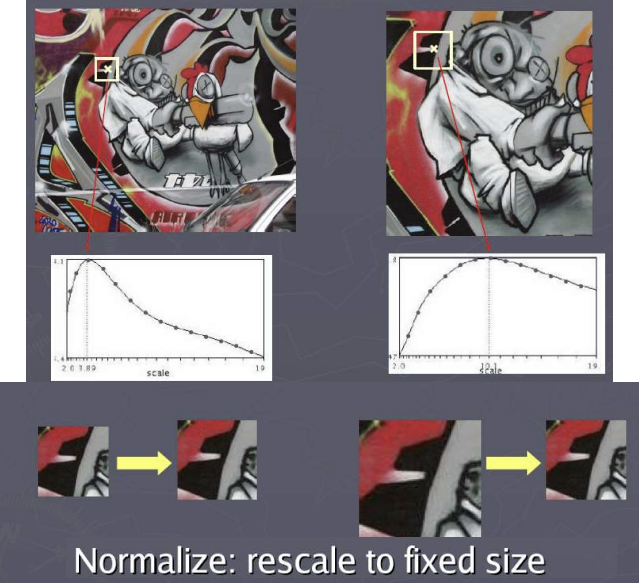
- 이미지 크기를 줄여가는 Gaussian pyramid를 만들어서 각 단계에 대해 harris corner를 찾은 뒤 같은 부분이라고 예측되는 부분에서 responce가 가장 큰 부분 킵! (또는 threshold로 여러개를 킵하기도 함)
- Gaussian pyramid가 window 크기 키우는 것보다 빠름
+) f를 구하는 다른 방법: Laplacian of Gaussian (LOG)
- 자신과 주변이 얼마나 차이나는지..
- 근데 아무도 안쓰니까 넘어가~~
2. Creating Descriptors
- Descriptors: local한 feature points가 어떻게 생겼는가
- 두 이미지에서 비슷한 descriptor를 가지는 feature point를 matching
- transformation에 상관없이 똑같은 feature를 찾는게 목표
transformational invariance
- 대부분 feature methods는 uniform transform(Translation, 2D rotation, scale)에 invariant함
- 제한된 nonuniform도 invariant함
- limited 3D rotations (SIFT는 60도까지)
- limited affine transformations
- limited illumination/contrast changes
- uniform transform과 일부 nonuniform transform에서는 matching을 할 수 있다
- detector(ex-Harris detector)와 descriptor가 invariance 해야지 matching을 할 수 있다
- detector가 invariance해야지 두 이미지에서 같은 부분의 feature point를 찾아낼 수 있는거고
- descriptor도 invariance해야지 두 feature point가 정말 같은 부분인지 비교를 할 수 있는 것
1. Multiscale Oriented PatcheS (MOPS) descriptor
- Rotation, Scaling, Photometric invariance for feature descriptors
- Oriented Patchs descriptor 만드는 법
- feature point에서 image patch의 dominant orientation을 eigenvector
x+방향으로 설정(eigenvector가 rotation에 invarient함을 이용)
- detected feature에 위치하는 40x40 window는 너무 많은 정보가 들어있으므로 sampling(5x5씩 평균)
- 이미지가 회전되거나 하면 픽셀이 그대로 유지되긴 힘듦 (이후에 나오는 내용) 그래서 생기는 문제점을 보완하기 위해 subsampling(작게만듦)
- 8x8 window로 sampling하고 주 축을 x방향으로 rotate ->
rotation invariant - 가장 밝은 픽셀값을 1, 어두운 것을 0으로 설정하는 Intensity normalize (gain, bias 없애기) ->
photometric invariant- 가장 밝은 픽셀값과 가장 어두운 픽셀값의 차이로 전체를 나눈 다음, 가장 어두운 픽셀값으로 전체 빼기
- 또는, 가장 어두운 픽셀값으로 전체를 뺀 다음, 그 때의 차이로 나누기
- 산포도(standard deviation)를 계산해서 그거만큼 scaling해서 비슷한 범위로 맞춘다 ?

- feature point에서 image patch의 dominant orientation을 eigenvector
- Oriented Patchs descriptor의 mulitple scale로 detection -> MOPS ->
scaling invariant- 실제로는 window크기 말고 이미지 크기로 조절
- 아래 이미지는 5개 레벨의 피라미드

2. Scale Invariant Feature Transform (SIFT) descriptor
- detected feature에 patch (16x16 window)
- 각 픽셀의 edge 방향 계산 (gradient의 수직)
- window를 4등분 -> 4개의 4x4 grid
- treshold로 약한 edge를 버리고, 각 grid의 edge 방향에 대한 histogram 생성 (histogram을 feature, edge들의 방향 분포를 descriptor라고 할 것)
- histogram은 [0~2π]를 8개의 방향으로 나눠서 아래 그림 처럼 나타남
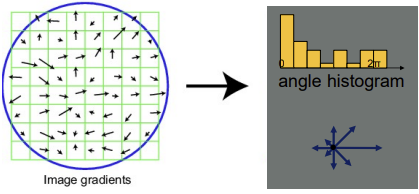
- 이걸 각 grid마다 나타내면 아래와 같고, 16cell * 8 orientations = 128 dimensional descriptor -> 각 grid마다 128개의 descriptor가 나온다
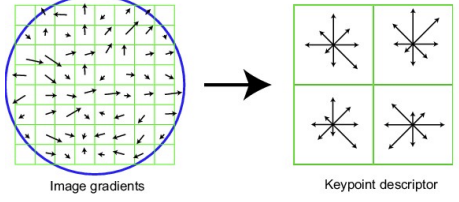
- histogram은 [0~2π]를 8개의 방향으로 나눠서 아래 그림 처럼 나타남
- SIFT는 매우 강력한 matching 기술
- 3D rotation invariant
- view point가 바꼈을 때 (plane rotation; 60도까지)
- illumination 변화(낮, 밤)가 클 때도 잘 됨
- 빠르고 효율적(실시간)

- 3D rotation invariant
❗MOPS는 rotation, scaling, photometric한 것에 대해 invariant를 가지고, SIFT는 추가로 3D rotation에 대해서도 invariant하다
+) Binary descriptor
- 밝기만 비교
- 특정 픽셀 중심으로 구역들을 만든 뒤, 그 구역들의 밝기 비교해서 다른 구역보다 어두우면 0, 밝으면 1 (bit 단위 descriptor)
- matching을 하기 위해 bit값이 같지 않은 자리의 개수를 세는 hamming distance를 사용
Distance
- descriptor마다 사용하는 distance 종류가 다르다 (하지만 주로 L2)
- L1: 절댓값의 합
- L2: 제곱의 합 (MOPS, SIFT)
- Hamming distance: 같지 않은 bit 개수 (Binary descriptor)
3. Feature Matching
- feature points 중 비슷한 descriptor를 가지면 matching
- 이미지 I1과 I2를 비교하는 경우, I1의 한 feature point의 descriptor와 I2의 모든 feature points의 descriptor를 비교 (픽셀끼리)
- 그 중 descriptor간 거리(차이)가 가장 짧은 것과 매칭
- 꼭 한 쌍이 아닐 수 있음 (many to one)
Diffrenece between two features
- SSD(f1, f2)
- 두 descriptors의 SSD
- 양수로 만들고, 모든 범위에서 미분 가능하도록
- 차이를 더 강조해주는 효과도 있음
- 문제점: 비슷한게 많으면 애매한 match가 나올 수 있음 (-> sol: ratio distance)

- 두 descriptors의 SSD
- Ratio distance
SSD(f1, f2)/SSD(f1, f2')- f2는 f1과 SSD 차이 가장 적은 것(best SSD match)
- f2'는 f1과 두번째로 차이 적은 것(2nd best SSD match)
- 1, 2등의 비율인 ratio distance가 1과 가깝게 나오면 f1과 f2이 거의 동일한 것이므로 애매한 match로 인식해 사용하지 않음
(f1에 대응하는 점을 찾을 수 없다. 애매하다)
Threshold
- descriptor간 거리(차이)가 가장 짧은 것과 매칭할 때, 그 거리에 대한 threshold를 두어서 오류가 발생하는 것을 방지
(오류: diffrenece가 가장 작다고 해서 봤는데 같은 point가 아니여서 큼, 걍 큰 것들 중 젤 작은 것 뿐) - 또는 상위 n개의 매칭만 사용하는 등의 방법도 있으며 꼭 threshold로 끊는다기 보단, 필요한 정보를 충분히 획득한 뒤 버린다? 정도로 이해
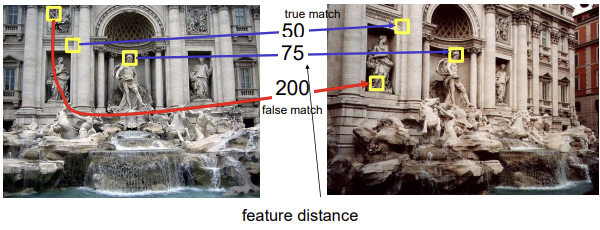
- 그럼에도 불구하고 잘못된 매칭이 있을 수 밖에
- True positives: 알맞게 매칭된 것의 개수 -> 최대화 해야함
- False positives: 잘못 매칭된 것의 개수 -> 최소화 해야함
- False positives를 줄이려고 threshold를 사용하면 True positives도 같이 줄어든다 -> threshold를 어떻게 정해야할까?
- 다양한 threshold로 테스트하여 그래프로 나타내본다 (ROC)
ROC(Receiver Operator Characteristic) curve
- 다양한 threshold로 테스트해서 나온 분포로 matching 알고리즘이 잘 만들어질수록 코너에 가까운 곡선
- ideal한 알고리즘이라면 ┌ 형태,..이고 가장 나쁜 알고리즘은 대각선으로 아래로 볼록한 곡선은 없음
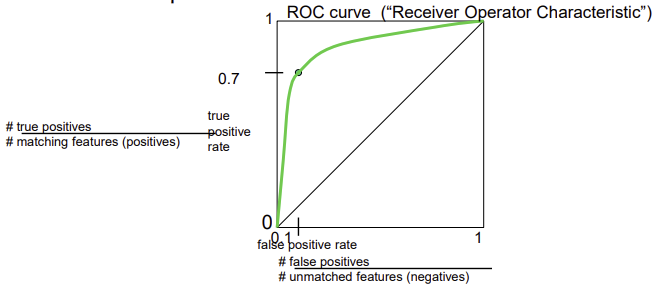
- 세로축: true positive rate(recall) =
true positives/matching features
(매칭된 것 중에 알맞게 매칭된 것의 비율; 정답률) - 가로축: false positive rate(1-precision정확도) =
false positives/unmatched features
(매칭되지 않은 것 중에 잘못 매칭된 것의 비율)]
Features are used for
- Image alignment: 여러개의 이미지 붙여서 mosaics 만들기
- 3D reconstruction 여러개의 이미지로 3차원 재구성
- Motion tracking: 카메라의 extrinsics인 transform 정보 알아내기 -> AR
(feature matching을 실시간으로 하면서 카메라가 어떻게 움직이는지 추정) - Object recognition
- Indexing and database retrieval
- Robot navigation