자료 구조 (Data Structure)
데이터는 실생활을 구성하고 있는 모든 값. 이 데이터를 효율적으로 다룰 수 있는 방법
자료구조 시각화 자료
1. Stack
- 데이터를 순서대로 쌓는 구조
- LIFO(Last In First Out)
- FILO (First In Last Out)
- 데이터를 하나씩 넣고 뺄 수 있음
- 하나의 입출력 방향
- Stack 클래스는 Vector 클래스를 상속받아 구현
Vector 클래스는 배열을 사용하여 구현
데이터를 추가, 삭제할 경우 내부적으로 길이가 변경된 배열을 생성하여 복제
-> 데이터를 처리할때 맨 위의 데이터만 처리하기 때문에 빠름
장점
- 스택에 저장된 데이터를 가져오는 속도가 빠름
- 별도 구현 없이 제공되는 Stack 클래스 사용 가능
단점
- 크기 제한이 없음 -> 메모리 사용량이 불필요하게 증가할 수 있음
- Vector 클래스를 상속받은 메서드 중 일부를 오버라이딩으로 구현하여 스택의 의도된 동작을 방해할 수도 있음
괄호가 올바르게 짝지어져 있는지 확인
import java.util.*;
public class BracketCheker {
public static void main(String[] args) {
String s1 = "([])(){}";
String s2 = "([)]";
String s3 = "([](){([])})";
String s4 = "";
System.out.println(s1 + " is balanced? " + isBalanced(s1)); // ([])(){} is balanced? true
System.out.println(s2 + " is balanced? " + isBalanced(s2)); // ([)] is balanced? false
System.out.println(s3 + " is balanced? " + isBalanced(s3)); // ([](){([])}) is balanced? true
System.out.println(s4 + " is balanced? " + isBalanced(s4)); // is balanced? true
}
public static boolean isBalanced(String s) {
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(' || c == '{' || c == '[') {
stack.push(c);
}
else if (c == ')' || c == '}' || c == ']') {
if (stack.isEmpty()) return false;
char top = stack.pop();
if (c == ')' && top != '(' || c == '}' && top != '{' || c == ']' && top != '[')
return false;
}
}
return stack.isEmpty();
}
}LinkedList로 구현한 Stack
장점
- 동적으로 메모리 할당 -> 스택의 크기를 동적으로 조절
- 크기와 관계없이 일정한 시간 복잡도
단점
- 앞뒤 요소를 가리키는 포인터가 추가되어 메모리 사용량이 더 큼
Array로 구현한 Stack
장점
- 메모리 사용량이 적음
- 인덱스로 요소에 바로 접근 가능
단점
- 크기가 고정되어 있어 크기를 조절해야 할 경우 배열을 복사해야함 -> 크기가 커질수록 성능 저하
2. Queue
- 들어온 순서대로 나옴
- FIFO / LILO
- enqueue / dequeue
- 데이터는 하나씩 넣고 뺄 수 있음
- 두 개의 입출력 방향
장점
- 먼저 넣은 순서대로 데이터를 처리할때 유용
- 삽입과 삭제가 양 끝에서 이루어져 속도가 빠름
단점
- 중간에 있는 데이터를 처리해야 할때는 적합하지 않음
- 크기제한이 없어 메모리 낭비 발생 가능
- iterator()가 지원되지 않음
- remove() 메서드를 사용할때 queue에 중복된 객체가 있을 때 어떤 객체가 삭제되는지 명확하지 않음
문자열을 입력받아 한 문자를 출력하고 다음 문자를 큐에 넣고를 반복하는 프로그램
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
public class StringTransformation {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String str = br.readLine();
System.out.println(transform(str));
}
static String transform (String str) {
StringBuilder sb = new StringBuilder();
Queue<Character> que = new LinkedList<>();
for (char c : str.toCharArray()) {
que.offer(c);
}
while (!que.isEmpty()) {
sb.append(que.poll());
if (que.isEmpty()) break;
que.offer(que.poll());
}
return sb.toString();
}
}3. Tree
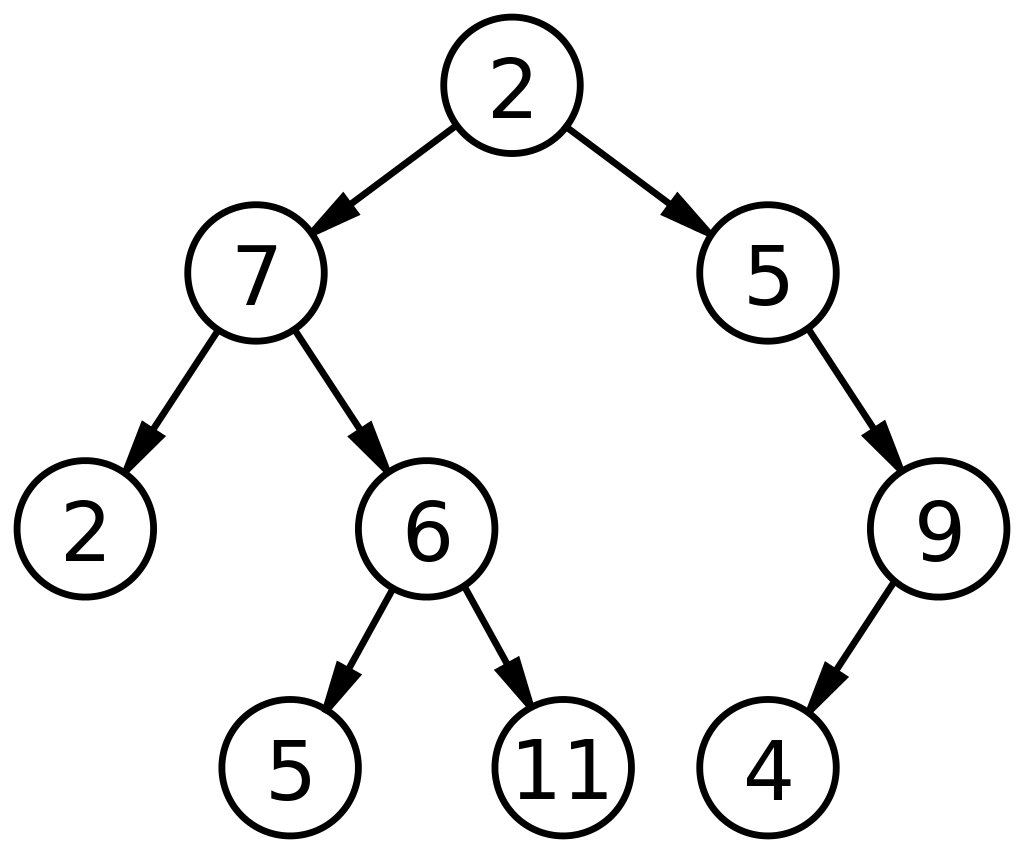
*크기가 9, 높이가 3인 이진 트리
- 단방향 그래프의 한 구조
- 하나의 데이터 아래에 여러개의 데이터가 존재할 수 있는 비선형 구조
- 용어
- 노드(Node) : 트리 구조를 이루는 모든 개별 데이터
- 루트(Root) : 트리 구조의 시작점이 되는 노드
- 부모 노드(Parent Node) : 두 노드가 상하 관계로 연결 되어 있을 때 루트에서 가까운 노드
- 자식 노드(Child Node) : 두 노드가 상하 관계로 연결 되어 있을 때 루트에서 가까운 노드
- 리프(Leaf) : 트리 구조의 끝 지점, 자식 노드가 없는 노드
- 깊이(depth) : 루트로부터 특정 노드까지의 깊이 // 루트는 깊이가 0
- 레벨(level) : 같은 깊이의 노드를 묶어 레벨로 표현. 같은 레벨에 나란히 있는 노드는 형제 노드(Sibling Node)
- 높이(height) : 리프 노드를 기준으로 루트까지의 높이 // 기준이 되는 리프 노드의 높이는 0
- 서브 트리(Sub tree) : 루트로부터 뻗어 나온 큰 트리의 내부에 트리 구조를 갖춘 작은 트리
- 장점 :
- 계층 구조를 나타내는데 효과적
- 정렬과 탐색에 활용 가능
- 삽입가 삭제가 쉬움 -> 해당 노드의 부모와 자식 노드만 수정하면 되기 때문
- 시각화가 쉬워 구조 파악에 용이
Binary Tree
자식 노드가 최대 두 개인 노드들로 구성된 트리
왼쪽 자식 노드와 오른쪽 자식 노드
- 정 이진 트리(Full binary tree)
: 각 노드가 0개 혹은 2개의 자식노드를 가짐 - 완전 이진 트리(Complete binary tree)
: 마지막 레벨을 제외한 모든 노드가 가득 차 있고 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져 있어야 함 - 포화 이진 트리(Perfect binary tree)
: 정 이진 트리이면서 완전 이진 트리인 경우
모든 레벨이 가득 채워져 있는 트리
Binary Search Tree
이진 탐색의 속성이 이진 트리에 적용된 형태의 이진 트리
이진 탐색이란
정렬된 데이터 중 특정한 값을 찾기 귀한 탐색 알고리즘 중 하나.
오름차순으로 정렬된 데이터를 같은 크기의 두 부분으로 나눈 후 두 부분 중 탐색이 필요한 부분에서만 탐색범위를 제한하여 원하는 값을 찾음
1. 전체 데이터에서 중간(root)에 찾고자 하는 값이 있는지 확인
2. 중간값이 찾고자 하는 값이 아닐 경우, 오름차순으로 정렬된 데이터에서 중간값보다 큰값인지 작은값인지 판탄
3. 찾고자 하는 값이 중간값보다 작을 경우 데이터의 맨 앞에서 중간값 전까지의 범위를 반복 탐색
4. 찾고자 하는 값이 중간값보다 클 경우, 데이터의 중간값의 다음 값부터 맨 마지막까지 반복 탐색- 루트노드의 왼쪽엔 루트노드의 값보다 작은 값들이, 오른쪽엔 큰 값들이 있어야함
- 좌우 서브 트리가 모두 이진 탐색 트리여야 함
->모든 왼쪽 자식의 값이 루트와 부모보다 작고, 모든 오른쪽 자식의 값이 루트와 부모보다 큼
Tree Search Algorithm

import java.util.ArrayList;
public class Tree_traverse {
public static void main(String[] args) {
}
// 전위 순회(preorder traverse)
public ArrayList<String> preOrder(Node node, ArrayList<String> list) {
if (node != null) {
list.add(node.getData());
list = preOrder(node.getLeft(), list);
list = preOrder(node.getRight(), list);
}
return list;
// 탐색 종료 시 list의 값 -> ["A", "B", "D", "H", "I", "E", "J", "K", "C", "F", "L", "M", "G", "N", "O"]
}
// 중위 순회(inorder traverser)
public ArrayList<String> inOrder(Node node, ArrayList<String> list) {
if (node != null) {
list = inOrder(node.getLeft(), list);
list.add(node.getData());
list = inOrder(node.getRight(), list);
}
return list;
// 탐색 종료 시 list의 값 -> ["H", "D", "I", "B", "E", "J", "K", "A", "L", "F", "M", "C", "N", "G", "O"]
}
// 후위 순회(postorder traverse)
public ArrayList<String> postOrder(Node node, ArrayList<String> list) {
if (node != null) {
list = postOrder(node.getLeft(), list);
list = postOrder(node.getRight(), list);
list.add(node.getData());
}
return list;
// 탐색 종료 시 list의 값 -> ["H", "I", "D", "J", "K", "E", "B", "L", "M", "F", "N", "O", "G", "C", "A"]
}
}
class Node {
String data;
Node left;
Node right;
public Node(String data) {
this.data = data;
}
public Node getLeft() {
return left;
}
public String getData() {
return data;
}
public Node getRight() {
return right;
}
}4. Graph

*3개의 정점, 3개의 간선으로 이루어진 그래프
- 용어
- 정점(vertex) : 노드, 데이터가 저장되는 기본 원소
- 간선(edgo) : 정점 간의 관계, 정점을 이어주는 선
- 인접 정점(adjacent vertex) : 하나의 정점에서 간선으로 직접 연결되어 있는 정점
- 가중치 그래프(weighted Graph) : 연결의 강도(추가 정보)가 적혀 있는 그래프
- 비가중치 그래프(unweighted Graph) : 연결의 강도가 적혀 있지 않은 그래프
- 무향(무방향) 그래프(undirected Graph) : 양쪽으로 이루어진 간선 <=> 단방향 그래프
- 진입차수(in-degree)/진출차수(out-degree) :
한 정점으로 들어오는 간선, 나가는 간선의 수 - 인접(adjacency) : 간선으로 직접 이어진 정점
- 자기 루프(self loop) : 정점에서 진출한 간선이 곧바로 자신에게 진입하는 경우
- 사이클(cycle) : 한 정점에서 출발해 다시 해당 정점으로 돌아갈 수 있을때 사이클이 있다고 표현
rmfladsafsdfadsfadsfasdfasdf
// 인접 행렬 // 가중치 그래프라면 1대신 의미있는 값으로
int[][] matrix = new int[][] {
{0, 1, 0},
{0, 0, 1},
{1, 1, 0}
};
// 인접 리스트 -> 인접 행렬보다 상대적으로 메모리를 덜 차지
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
graph.add(new ArrayList<>(Arrays.asList(1, null)));
graph.add(new ArrayList<>(Arrays.asList(2, null)));
graph.add(new ArrayList<>(Arrays.asList(0, 1, null)));
}Graph Search Algorithm
- 모든 정점을 방문하는 것이 목적인 경우 두 방법 모두 가능
- 최단 거리 -> BFS
- 규모가 크지 않고 원하는 대상이 멀지 않은 경우 -> BFS
- 경로의 특징을 저장해야 하는 경우 (장애물이 있는 경우 포함)
-> DFS - 미로 생성 -> DFS
- 검색 대상 그래프가 매우.. 클 경우 -> DFS
BFS(Breadth-First Search)
너비 우선 탐색 / 큐를 활용하여 구현
1. 하나의 정점을 기준으로 해당 정점과 인접한 정점을 모두 방문
2. 기준점을 방문한 정점으로 변경하여 해당 정점에 인접한 정점을 방문 반복
-
최단 경로 탐색에 유리 // 인접한 정점들을 먼저 방문하기 때문
-
Queue 자료 구조를 사용하여 방문한 정점들을 큐에 저장, 그래프의 크기가 크면 많은 메모리를 사용
- 시작노드를 큐에 삽입 후 큐가 빌때까지 반복 시작
- 큐에서 현재 정점을 가져옴
- 현재 정점의 방문 여부를 체크
- 현재 정점과 인접한 정점을 모두 큐에 삽입
- 그래프 끝까지 반복
-
시작 정점에서 도달할 있는 정점만 탐색
-
방문 여부를 체크하는 자료구조를 사용해야 함
-
활용 시 주의 사항
- 방문 여부 체크(보통 boolean형 배열)
- 큐 활용
- 최단 경로 탐색(경우에 따라 거리를 기록할 변수 사용)
- 메모리 공간
-
BFS 예제 템플릿
/**
* BFS 인접행렬 : 너비 우선 탐색을 구현한 템플릿 예제입니다.
*
* @param array : 각 정점을 행/열로 하고, 연결된 정점은 1로, 연결되지 않은 정점은 0으로 표기하는 2차원 배열
* @param visited : 방문여부 확인을 위한 배열
* @param src : 방문할 정점
* @param result : 방문했던 정점 리스트를 저장한 List
*
**/
public ArrayList<Integer> bfs_array(int[][] array, boolean[] visited, int src, ArrayList<Integer> result) {
//bfs의 경우 큐를 사용합니다.
Queue<Integer> queue = new LinkedList<>();
//시작 지점을 큐에 넣어주고, 해당 버택스의 방문 여부를 변경합니다.
queue.offer(src);
visited[src] = true;
//큐에 더이상 방문할 요소가 없을 경우까지 반복합니다.
while (!queue.isEmpty()) {
//현재 위치를 큐에서 꺼낸 후
int cur = queue.poll();
// 현재 방문한 정점을 result에 삽입합니다.
result.add(cur);
//전체 배열에서 현재 버택스의 행만 확인합니다.
for (int i = 0; i < array[cur].length; i++) {
//길이 존재하고, 아직 방문하지 않았을 경우
if(array[cur][i] == 1 && !visited[i]) {
//큐에 해당 버택스의 위치를 넣어준 이후
queue.offer(i);
//방문 여부를 체크합니다.
visited[i] = true;
}
}
}
//이어진 모든 길을 순회한 후 방문 여부가 담긴 ArrayList를 반환합니다.
return result;
}- 예제 코드
public class BFS { // 두 노드 사이의 최단 경로 찾기
public static void main(String[] args) {
int [][] graph = {
{0, 1, 1, 0, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 0, 0, 1},
{0, 1, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 1},
{0, 0, 1, 0, 1, 0}
};
int start = 0;
int end = 5;
System.out.print(shortestPath(graph, start, end));
}
static ArrayList<Integer> shortestPath(int [][] graph, int start, int end) {
boolean[] visited = new boolean[graph.length]; // 방문 여부 체크를 위한 배열
return bfs(graph, start, end, visited);
}
static ArrayList<Integer> bfs (int[][] graph, int start, int end, boolean[] visited) {
Queue<Integer> que = new LinkedList<>();
int[] parent = new int[graph.length];
que.offer(start); // 현재 정점 삽입
visited[start] = true;
parent[start] = -1; // 시작 지점 표시
while (!que.isEmpty()) {
int node = que.poll();
if (node == end) { // 도착점 도달했을 때
ArrayList<Integer> path = new ArrayList<>();
while (node != -1) {
path.add(node);
node = parent[node];
}
Collections.reverse(path);
return path;
}
for (int i = 0; i < graph.length; i++) { // 도착점 도달 전
if (graph[node][i] == 1 && !visited[i]) { // 현재 정점의 인접한 정점 중 방문하지 않은 정점을 큐에 삽입
que.add(i);
visited[i] = true;
parent[i] = node;
}
}
}
return null;
}
}DFS(Depth-First Search)
깊이 우선 탐색 / 스텍, 재귀를 이용하여 구현
-
한 분기를 탐색 후 다음 분기로 넘어가기 전 해당 분기를 완전히 탐색
-
탐색 불가능한 상태가 되면 이전 분기로 돌아와 다음 분기 탐색
- 모든 정점을 완전히 탐색 가능 -> 첫 번째 경로에 찾아야 하는 정점이 있는 경로여도 다른 모든 경로를 탐색
- 현 경로상의 정점만 기억하여 저장 공간 수요가 비교적 작고 목표 정점이 깊은 단계에 있으면 빨리 구할 수 있음
-
순환구조 고려 방문 정점을 다시 방문하지 않도록 해야함
- 도달할 정점이 없을 시 무한 루프에 빠질 수 있음 -> 지정한 임의의 깊이까지 탐색 후 목표 정점
- 찾아낸 경로가 최단 경로란 보장이 없음 // 목표한 정점에 다다르는 순간 탐색 종료
- 구현 방법
- 일반적으로 재귀를 통해 구현
- 방문했던 정점인지 확인, 방문 했다면 재귀 호출을 종료
- 방문하지 않았다면 방문 여부 체크
- 해당 정점에 연결된 모든 정점을 재귀 호출로 순회
- DFS 예제 템플릿
/**
* DFS 인접행렬 : 깊이 우선 탐색을 구현한 템플릿 예제입니다.
*
* @param array : 각 정점을 행/열로 하고, 연결된 정점은 1로, 연결되지 않은 정점은 0으로 표기하는 2차원 배열
* @param visited : 방문 여부 확인을 위한 배열
* @param src : 방문할 정점
* @param result : 방문했던 정점 리스트를 저장한 List
*
**/
public ArrayList<Integer> dfs(int[][] array, boolean[] visited, int src, ArrayList<Integer> result) {
// 이미 방문했다면
if (visited[src] == true) {
result.add(src); // 방문한 정점을 저장
return result; // 저장한 데이터를 반환하며, 재귀호출을 종료
}
// 아직 방문하지 않았다면
visited[src] = true; // 방문한 정점을 표기
// 현재 정점에서 이동할 수 있는 정점을 순회하며 재귀 호출
for (int index = 0; index < array.length; index++) {
if (array[src][index] == 1) {
// 재귀 호출을 통해, 방문 여부를 담은 데이터를 반환과 동시에 할당
result = dfs(array, visited, index, result);
}
}
return result;
}- 예시 코드
public class getDirections_dfs {
public static void main(String[] args) {
int[][] matrix = new int[][] { // 인접 행렬이 담긴 2차원 배열
{0, 1, 0, 0},
{0, 0, 1, 0},
{0, 0, 0, 1},
{0, 1, 0, 0},
};
System.out.print(getDirections(matrix, 1, 4));
// 주어진 정점으로 다른 정점으로 이어지는 길이 존재하는지 여부를 반환
}
static boolean getDirections(int[][] matrix, int from, int to) {
// from, to -> 행
boolean[] visited = new boolean[matrix.length];
return dfs(matrix, from, to, visited);
}
static boolean dfs (int[][] matrix, int cur, int to, boolean[] visited) {
if (cur == to) return true; // 현재 노드의 갚이 원하는 값일때 리턴
visited[cur] = true; // 현재 방문한 곳을 true로
for (int i = 0; i < matrix.length; i++) {
if (matrix[cur][i] == 1 && !visited[i]) { // 연결된 노드가 있을때 해당 노드로 재귀 진입
if (dfs(matrix, i, to, visited)) return true;
}
}
return false; // 연결된 노드를 확인했는데 원하는 값이 없이 끝났을때 false 리턴
}
}import java.util.*;
public class ConnectedVertices_dfs {
public static void main(String[] args) {
int[][] edges = new int[][]{ // 시작과 도착 정점이 담겨있는 배열 {시작 정점, 도착 정점} 간선으는 무향
{0, 1},
{2, 3},
{4, 5}
};
System.out.print(connectedVertices(edges));
}
static int connectedVertices(int[][] edges) {
int rc = Arrays.stream(edges).flatMapToInt(Arrays::stream).max().getAsInt() + 1;
int[][] graph = new int[rc][rc]; // 인자로 받은 배열의 요소중 가장 큰 정점을 기준으로 1칸 더 큰 정사각형의 행렬을 생성
for (int i = 0; i < edges.length; i++) { //생성한 graph 배열에 인자로 전달받은 edges의 연결된 정점들의 값에 1을 할당
graph[edges[i][0]][edges[i][1]] = 1;
graph[edges[i][1]][edges[i][0]] = 1;
}
int count = 0;
boolean[] visited = new boolean[rc]; // 해당 행을 방문했는지 체크하기 위한 boolean 배열
for (int i = 0; i < rc; i++) {
if (!visited[i]) {
dfs(graph, i, visited); // 재귀 함수 탈출 후 count + 1
count++;
}
}
return count;
}
static void dfs(int[][] graph, int row, boolean[] visited) {
visited[row] = true;
for (int i = 0; i < graph.length; i++) { // 인자로 받은 행의 열을 돌며 연결된 노드가 있고 해당 노드의
if (graph[row][i] == 1 && !visited[i]) // 행을 다녀온 적이 없으면 해당 열에 해당하는 행으로 재귀
dfs(graph, i, visited);
}
}
}