Time Complexity
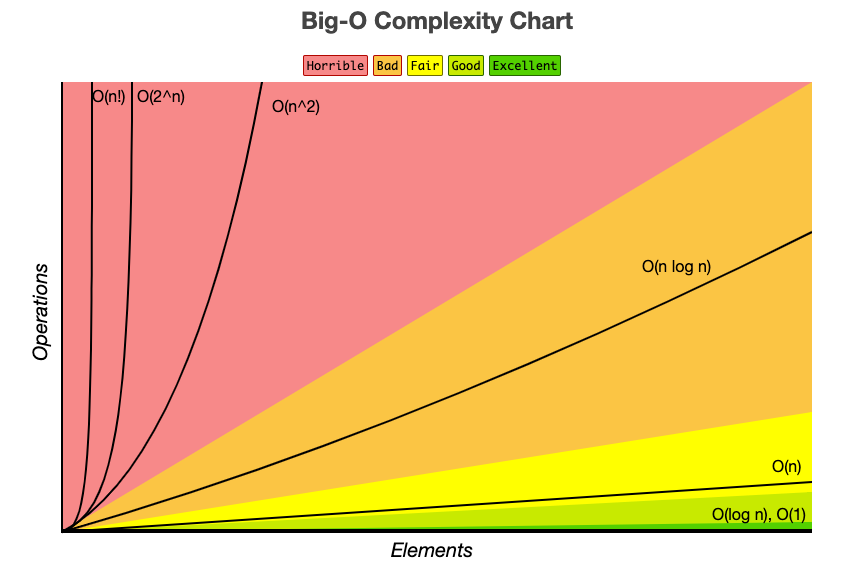
입력값에 따라 알고리즘의 시간 복잡도가 어떻게 변화하는지를 나타냄
- Big-O : 최악의 경우
- Big-Ω : 평균의 경우
- Big-θ : 최선의 경우
1. O(1)- 상수 시간 복잡도 :
입력 크기와 관계없이 실행 시간이 일정하게 유지
int a = 1;
int b = 2;
int c = a + b;ex) 배열 탐색
2. O(log n) - 로그 시간 복잡도 :
반복문을 실행될 때마다 탐색할 양이 반으로 줄어드는 경우
// 이진 탐색 알고리즘
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1; // 찾지 못한 경우
}3. O(n) - 선형 시간 복잡도 :
입력값이 증가함에 따라 시간 또한 같은 비율로 증가
// 반복문
int n = 100;
for (int i = 0; i < n; i++) {
System.out.println(i);
}4. O(n^2) - 이차 시간 복잡도 :
입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가
//2중 반복문
int n = 100;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println(i + " " + j);
}
}5. O(nlogn) - 로그 선형 시간 복잡도 :
입력값이 증가함에 따라 수행시간이 로그 함수와 선형 함수의 곱으로 증가
int n = 100;
for (int i = 0; i < n; i++) {
for (int j = 1; j < n; j *= 2) {
System.out.println(i + " " + j);
}
}6. O(2^n) - 지수 시간 복잡도 :
입력값이 증가함에 따라 수행 시간이 2의 n제곱으로 증가
int fib(int n) {
if (n <= 1) {
return n;
} else {
return fib(n - 1) + fib(n - 2);
}Algorithm
pseudocode
프로그래밍 언어로 코드를 작성하기 전 일상 언어로 프로그램 작동 원리를 먼저 작성하는 것
- 코드 작성 시간 단축
- 디버깅에 용이
- 다른 사람이 로직을 이해하는데 도움
1. Greedy
- 선택 절차(Selection Procedure) : 현재 상태에서 최적의 해답을 선택
- 적절성 검사(Feasibility Check) : 선택한 해가 문제의 조건을 만족하는지 검사
- 해답 검사(Solution Check) : 원래의 문제가 해결되었는지 검사하고 해결되지 않았다면 선택 절차로 돌아가 반복
BOJ 13305 주유소
연습을 위해 백준 13305번 문제를 풀어보았다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
//https://www.acmicpc.net/problem/13305
public class BJ_13305 { // 주유소 // 58점
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
String[] dis = br.readLine().split(" ");
String[] oil = br.readLine().split(" ");
oil[oil.length - 1] = "1000000000";
long totalPrice = 0;
for (int i = 0; i < dis.length - 1; i++) {
long curPrice = Long.parseLong(oil[i]);
long nextPrice = Long.parseLong(oil[i + 1]);
long distance = Long.parseLong(dis[i]); // 다음 도시까지 가야하는 거리
if (curPrice > nextPrice) { // 다음 주유소 가격이 더 쌀때
totalPrice += distance * curPrice;
}
else { // 지금 가격이 다음 가격보다 쌀때
distance = 0; // j 인덱스 도시까지 가야하는 거리
for (int j = i + 1; j < oil.length; j++) { // 더 싼 주유소가 나올때까지 거리를 더함
nextPrice = Long.parseLong(oil[j]); // 다음에 나올 기름 가격
if (nextPrice < curPrice || j == oil.length - 1) { // 더 싼 주유소가 나오거나 마지막까지
distance += Long.parseLong(dis[j - 1]); // 비교했는데 지금이 제일 쌀때
break; // j = i + 1 해서 인덱스 한칸씩 더 밀림
}
else distance += Long.parseLong(dis[j - 1]);
i++;
}
totalPrice += distance * curPrice;
}
}
System.out.print(totalPrice);
}
}도시의 개수, 두 도시를 연결하는 도로의 길이, 각 도시 주유소의 기름값을 입력받고 제일 왼쪽 도시에서 제일 오른쪽 도시로 가는 최소 비용을 출력하는 문제이다.
도로의 길이와 도시별 주유소의 기름값을 하나의 문자열로 입력받고 공백을 기준으로 배열로 나누었다.
현재 있는 도시의 기름값이 다음 도시의 기름값보다 쌀 경우, 다음 도시의 기름값이 더 비쌀 경우로 나누었다.
다음 도시의 기름값이 더 비쌀 경우 반복문을 통해 현재 도시보다 기름값이 더 싼 도시를 찾으며 도시들의 거리를 더해준 뒤 가격이 더 싼 도시를 찾거나, 도착지까지 더 싼 주유소가 없으면 현재 도시의 기름값에 지금까지 더한 거리를 곱해주었다.
다음 도시의 기름값이 더 쌀 경우 다음 도시까지 가는데 필요한 기름만 넣고 다음 도시로 이동하여 다시 비교를 했다.
두번째 for문에서 기름값이 더 싼 주유소를 비교하는 동안 첫번째 for문의 i를 증가시켜주지 않아 디버깅하는데 한참 걸렸다..
몇가지 예제를 입력해보고 원하는 값이 나와 제출해보았는데 58점이다.
거리와 기름값 최대치가 1,000,000,000인데 이부분을 처리하지 못해서인 것 같다.
이 부분에 대해 좀더 공부를 해봐야겠다...
2. Simulation
모든 과정과 조건이 제시되어 그 과정을 거친 결과가 무엇인지 확인하는 유형
설명해준 로직 그대로 코드를 작성
3. Brute-Force
모든 가능성을 시도하여 문제를 해결하는 방법
- 공간복잡도, 시간복잡도를 고려하지 않음
- 사용할 수 있는 다른 알고리즘이 없을때
- 해결하는 여러 솔루션이 있고 각 솔루션을 확인할때
1. 순차 검색 알고리즘(Sequential Search)
배열 안에 특정한 값이 존재하는지 검색할 때 인덱스를 차례대로 검색
2. 문열 매칭 알고리즘(Brute-Force String Matching)
길이가 n인 전체 문자열이 길이가 m인 문자열 패턴을 포함하는지 검색
3. 선택 정렬 알고리즘(Selection Sort)
전체 배열을 검색하여 현재 요소와 비교하고 컬렉션이 완전히 정렬될 때까지 오름차순, 내림차순에따라 교환하는 정렬 알고리즘
4. Binary Search
- 정렬된 배열의 가장 중간 인덱스를 지정
- 찾으려고 하는 값이 지정한 중간 인덱스의 값이라면 탐색을 종료. 아니라면 3단계로 갑니다.
- 찾으려고 하는 값이 중간 인덱스의 값보다 큰 값인지, 작은 값인지 확인
- 값이 있는 부분과 값이 없는 부분으로 분리
- 값이 있는 부분에서 다시 1단계부터 반복
- 정렬된 배열에서 요소값을 효율적으로 검색할 때
- 데이터 양이 많을 수록 효율적
- 정렬된 배열에서만 구현 가능
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1; // 찾지 못한 경우
}5. Dynamic Programming
- memoization :
문제를 해결할 때 작은 문제들의 해를 저장해두고 나중에 다시 사용하여 문제를 해결 - tabulation :
작은 문제부터 해결하며 서서히 올라감 - 입력받은 순번의 피보나치 수를 DP를 이용하여 계산 후 출력하는 프로그램
import java.util.Scanner;
public class DP {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
long[] arr = new long[n + 1];
System.out.println(memoization(n, arr));
System.out.println(tabulation(n, arr));
}
// 푼 작은 문제를 저장 후 필요할 때마다 사용
static long memoization(int n, long[] arr) {
if (n == 1 || n == 2) return 1;
if (arr[n] != 0) return arr[n];
arr[n] = memoization(n - 1, arr) + memoization(n - 2, arr);
return arr[n];
}
// 가장 작은 문제부터 위로 서서히 올라감
static long tabulation (int n, long[] arr) {
arr[0] = 0;
arr[1] = 1;
for (int i = 2; i <= n; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[n];
}
}재귀함수로만 구현했을 경우 시간 복잡도가 O(2^n)이지만 DP를 사용하여 구현 하였을 경우 O(n)
Math
1. 순열(Permutation)
n개의 요소 중 순서에 따라 m개를 뽑는 경우의 수
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
public class Permutation { // 순열 : 요소 n개 중에 m개를 선택하여 순서에 상관있게 뽑는 경우의 수
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int num = Integer.parseInt(br.readLine()); // 입력받은 수 만큼 선택
String str = br.readLine();
String[] lookup = str.split(" ");
// for 문을 이용하여 순열의 경우의 수 구하기
ArrayList<String[]> forLoop = new ArrayList<>();
permutation1(lookup, forLoop);
for (String[] arr : forLoop) {
System.out.println(Arrays.toString(arr));
}
// 재귀를 이용하여 순열의 경우의 수 구하기
ArrayList<String[]> recursion = new ArrayList<>();
permutation2(lookup, new String[]{}, recursion, num);
for (String[] arr : recursion) {
System.out.println(Arrays.toString(arr));
}
}
// for 문을 이용하여 순열의 경우의 수 구하기
static void permutation1(String[] lookup, ArrayList<String[]> result) {
for (String item1 : lookup) {
for (String item2 : lookup) {
for (String item3 : lookup) {
// if (item1.equals(item2) || item2.equals(item3) || item3.equals(item1))
// continue; // 중복 제거
String[] input = new String[]{item1, item2, item3};
result.add(input);
}
}
}
}
// 재귀를 이용하여 순열의 경우의 수 구하기
static void permutation2(String[] lookup, String[] picked, ArrayList<String[]> result, int num) {
if (num == 0) {
result.add(picked);
return;
}
for (int i = 0; i < lookup.length; i++) {
String[] newPicked = Arrays.copyOf(picked, picked.length + 1);
newPicked[newPicked.length - 1] = lookup[i];
permutation2(lookup, newPicked, result, num - 1);
}
}
}위 코드 중 permutation1 메서드는 주어진 배열에서 3가지의 요소를 뽑아 만들 수 있는 순열을 구하는 코드이고 permutation2는 입력 받은 수만큼의 요소를 입력받은 문자들 중에서 뽑아 만들 수 있는 경우의 수를 모두 ArrayList에 담는다.
재귀를 사용하지 않으면 뽑아야 하는 요소의 수만큼 반복문이 중첩된다.
2. 조합(Combination)
n개의 요소 중 순서에 상관 없이 m개를 뽑는 경우의 수
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
public class Combination {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int num = Integer.parseInt(br.readLine());
String str = br.readLine();
String[] lookup = str.split(" ");
// for 문을 이용하여 조합의 경우의 수 구하기
ArrayList<String[]> forLoop = new ArrayList<>();
combination1(lookup, forLoop);
for (String[] arr : forLoop) {
System.out.println(Arrays.toString(arr));
}
// 재귀를 이용하여 조합의 경우의 수 구하기
ArrayList<String[]> combination = new ArrayList<>();
boolean[] isVisited = new boolean[lookup.length];
combination2(lookup, new String[]{}, combination, num, isVisited, 0);
for (String[] arr : combination) {
System.out.println(Arrays.toString(arr));
}
}
// for 문을 이용하여 조합의 경우의 수 구하기
static void combination1(String[] lookup, ArrayList<String[]> result) {
for (int i = 0; i < lookup.length; i++) {
for (int j = i + 1; j < lookup.length; j++) {
for (int k = j + 1; k < lookup.length; k++) {
String[] picked = {lookup[i], lookup[j], lookup[k]};
result.add(picked);
}
}
}
}
// 재귀를 이용하여 조합의 경우의 수 구하기
static void combination2(String[] lookup, String[] picked, ArrayList<String[]> result, int num, boolean[] isVisited, int idx) {
if (num == 0) { // 모든 요소를 골랐을 때
result.add(picked);
return;
}
for (int i = idx; i < lookup.length; i++) {
if (!isVisited[i]) { // 방문하지 않았다면
isVisited[i] = true;
String[] newPicked = Arrays.copyOf(picked, picked.length + 1);
newPicked[newPicked.length - 1] = lookup[i];
combination2(lookup, newPicked, result, num - 1, isVisited, i + 1);
isVisited[i] = false;
}
}
}
}순열보다 나왔던 조합들을 중복돼서 나오지 않게 하기 위해 재귀로 구현하기 껄끄러웠던 것 같다.
순열과 다른 점은 boolean타입 배열 isVisited를 사용하고 for문에 idx + 1이 아닌 i + 1 을 인자로 재귀함수에 넘겨주어 중복을 피하였다.
처음에 idx + 1을 해주었었는데 중복되는 조합들이 나왔었다. for문에서 반복을 하면서 i 값이 증가했어도 idx가 그대로여서 중복되는 조합들이 들어왔던 것 같다.
재귀가 너무 어렵다..
