Linear Regression
선형 회귀는 회귀 분석에 가장 기본적인 모델이다.
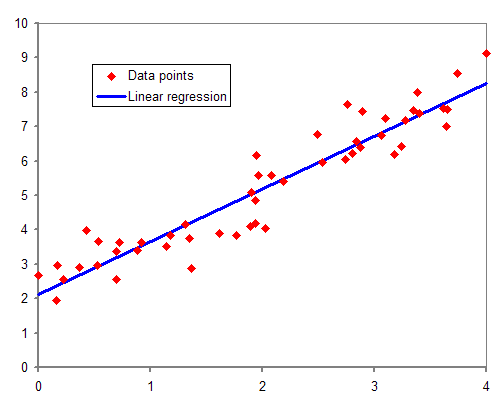
종속변수 y 와 한 개 이상의 독립변수 x와의 선형 상관관계를 모델링
선형 회귀는 데이터셋을 이용해 학습 과정을 거쳐 데이터에 가장 잘 맞는 선형 모델의 parameter를 찾아 회귀 분석을 실시한다.
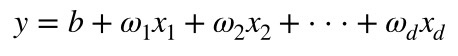
Cost function
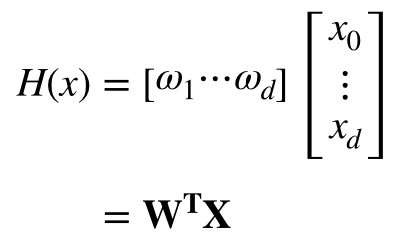
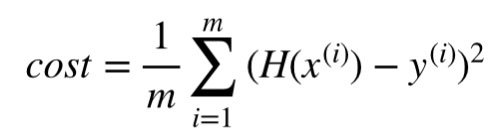
회귀
- MAE (평균 절대 오차)
- MSE (평균 제곱 오차)
- RMSE (평균 제곱근 오차)
분류
- Cross Entropy
Optimization
Gradient Descent (경사하강법)
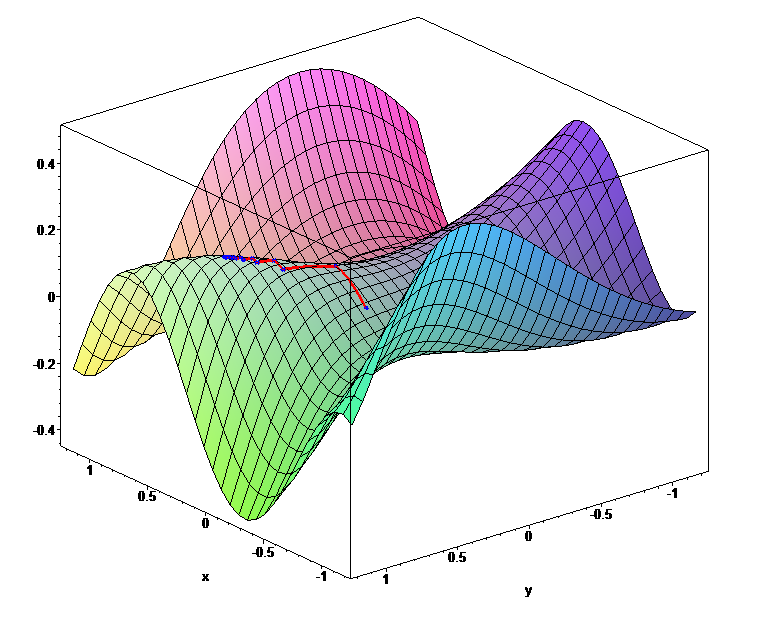
cost function을 이용해 가장 최적의 해 (오차를 가장 줄여줄 수 있는 해)를 찾는 과정이다.
기울기를 따라서 내려가면서 극소점에 도달할 때 최적의 해가 된다.
다만, 지역적인 최적해가 전역적인 최적해라고 보장할 수 없다.
- Learning Rate
현재 위치에서 기울기를 따라 이동할 거리를 정해준다. 학습률이 너무 작으면 반복을 매우 많이 진행해야 하므로 전역 최솟값을 도달하기 전에 모델이 학습을 중단할 수 있다. 반면, 학습률이 너무 크면 전역 최솟값을 넘어 반대로 올라가며 발산해 버릴 수 있다.
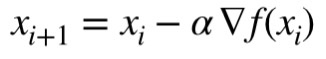
- Batch Gradient Descent
Gradient Descent를 위 cost function에서 구현하려면 가중치(W)에 대해 cost function의 경사를 편미분을 이용해 구해준다. 그 후 가중치를 update해준다. 이 때, 전체 데이터셋에 대한 계산을 매 iteration마다 진행해주므로 큰 데이터셋에서는 매우 오래 걸리게 된다. - Stochastic Gradient Descent
이에 대한 보완법으로 매 iteration마다 전체 데이터셋이 아닌 랜덤한 데이터 하나의 cost function을 이용해 경사를 계산하는 방법이다. 다만 Batch Gradient Descent 보다는 불안정하다. - Mini-Batch Gradient Descent
위 두 방법의 단점을 최소화하기 위해 랜덤한 데이터 하나가 아닌 작은 샘플 세트에 대해 cost function을 구하는 방법이다.
성능평가
MSE, R2 ...
가정
- 오차는 평균이 0이고 분산이 일정한 정규포를 가진다.
- 독립변수와 종속변수는 선형적인 상관관계를 갖는다.
- 오차항은 자기상관성이 없다.
- 데이터에 아웃라이어가 없다
- 독립변수와 오차항은 서로 독립이다.
- 독립변수 간에는 서로 선형적으로 독립이다.
Polynomial Regression (다항회귀)
독립변수와 종속변수가 선형적인 상관관계를 갖지 않을때
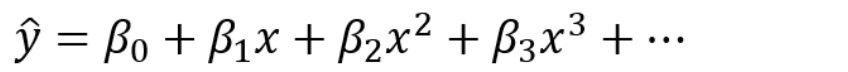
Robust Regression
데이터에 아웃라이어가 있을때
MSE 대신에 MAE
다중공선성에 의한 오버피팅 방지
Lasso Regression (L1 Regressioin)
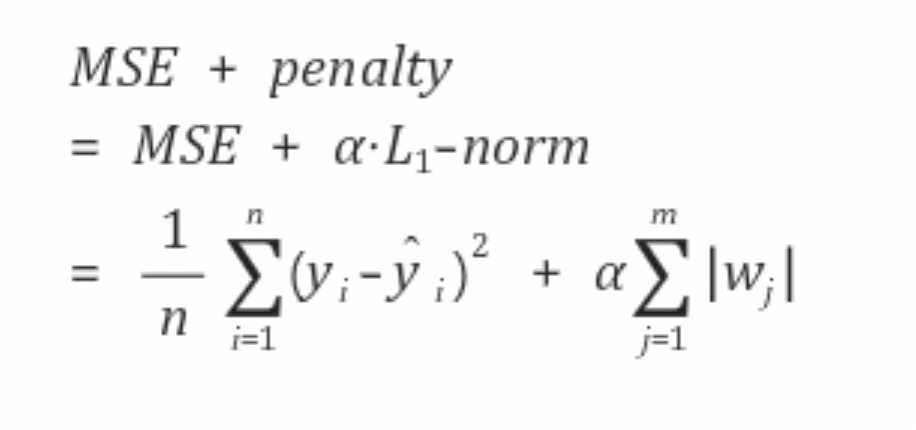
MSE에서 가중치가 0에 가깝게 하며 Regressioin
이 때 알파 * 페널티 함수 인데 알파로 Regression을 조절
Ridge Regression (L2 Regression)
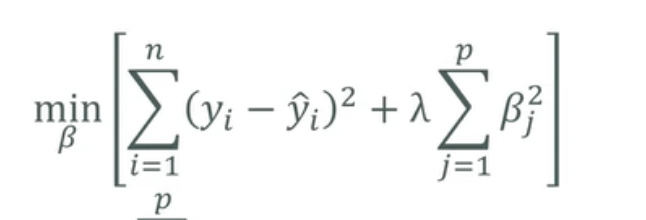
라쏘와 다르게 가중치의 절댓값의 합으로 Regression
