알고리즘 원리
- PCA는 기존의 변수들을 조합하여 서로 연관성이 없는 새로운 변수 PC를 생성한다. 이를 주성분이라고 한다.
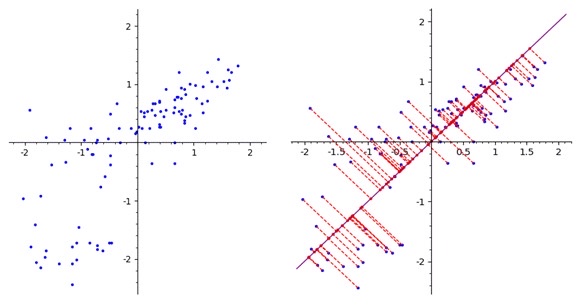
이해를 쉽게 하기 위해 변수가 2개인 2차원 평면의 데이터셋을 가정하자.
위 2개의 변수를 조합하여 데이터의 분포를 가장 잘 설명하는 하나의 새로운 변수를 생성하고 싶다. 이 때 새로운 변수 PC1 은 2차원의 데이터 포인트들을 하나의 축에 모두 정사영했을 때 분산이 가장 큰 벡터를 의미한다. - 2차원 -> 하나의 축 : 차원 축소
- 분산이 가장 큰 : 데이터의 분포를 가장 잘 설명
- 벡터 : PC1
두 번째 축(PC2)을 설정하는 것도 같은 원리로 분산이 가장 커지는 벡터로 설정하게 된다. 단, 처음에 설정했던 PC1과 관계가 없는 변수이어야 하므로 첫 번째 축과 수직하게 된다. 이러한 원리로 주성분들을 설정하고 차원을 축소할 수 있게 된다.
주성분 분석의 계산
python에서 실습
축구선수의 능력치를 데이터프레임화 시키고 PCA를 사용해서 차원을 축소 시켜보자!
데이터
'https://sofifa.com/players?showCol%5B0%5D=ae&showCol%5B1%5D=ta&showCol%5B2%5D=ts&showCol%5B3%5D=to&showCol%5B4%5D=tp&showCol%5B5%5D=td&showCol%5B6%5D=tg&showCol%5B7%5D=oa&col=oa&sort=desc'
위 링크에서 크롤링해 온 축구선수의 능력치 데이터를 이용
데이터프레임 형성 후 간단한 데이터프레임 형성
아래와 같은 데이터를 형성했다.
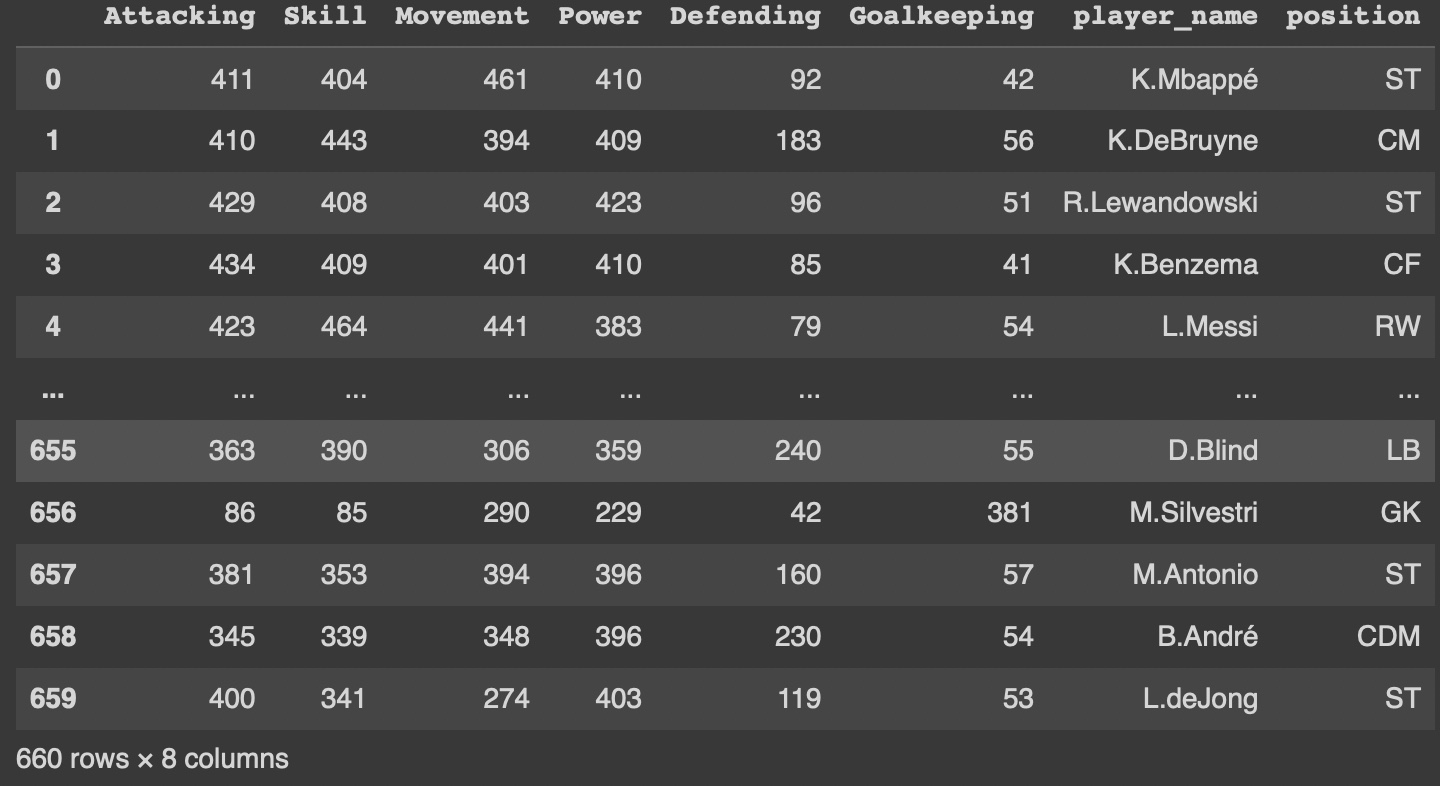
포지션 label 재설정
포지션의 개수가 너무 다양해서 크게 FW, MF, DF, GK로 나누었다.
new_position = []
for i in new_df['position']:
if i in ['ST', 'CF', 'LW', 'RW']:
new_position.append('FW')
elif i in ['CM', 'CAM', 'CDM', 'RM', 'LM']:
new_position.append('MF')
elif i in ['CB', 'LB', 'RB', 'RWB', 'LWB']:
new_position.append('DF')
else:
new_position.append('GK')
new_df['new_position'] = pd.DataFrame(new_position)PCA 적용
- 라이브러리 불러오기
from sklearn.decomposition import PCA- 주성분을 2개로 하는 PCA 모델 생성 및 fitting
pca = PCA(n_components = 2)
pca_model = pca.fit_transform(new_df[['Attacking', 'Skill', 'Movement', 'Power', 'Defending', 'Goalkeeping']])
new_df[['x', 'y']] = pca_model- 입력 인수
n_components : 축소 목표의 차원 개수 - 메서드
fit_transform() : 특징행렬을 낮은 차원의 근사 행렬로 변환
inverse_transform() : 변환된 근사행렬을 원래의 차원으로 복귀
- 데이터 시각화
sns.scatterplot(x = 'x', y = 'y', hue = 'new_position', data = new_df)
plt.show()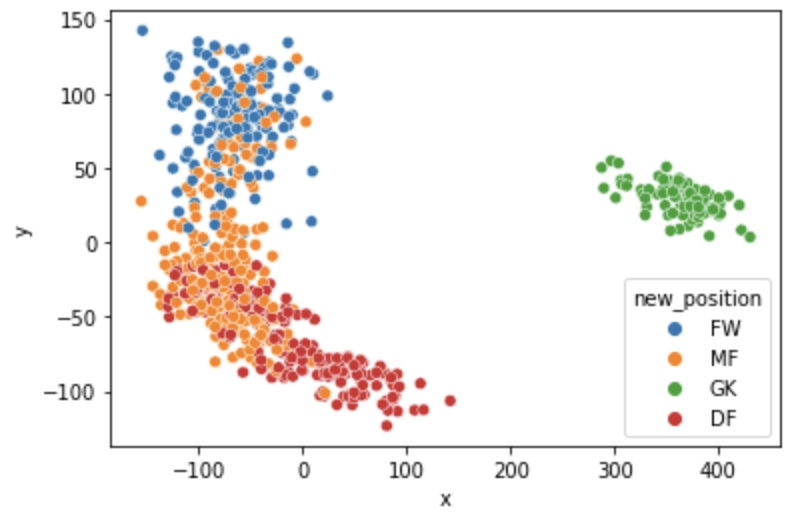
'Attacking', 'Skill', 'Movement', 'Power', 'Defending', 'Goalkeeping' 6개의 feature를 갖고 있는 Dataset이 주성분 'x', 'y'로 차원축소 되었음을 볼 수 있다.
스케일링은 왜 하는걸까?
머신러닝, 딥러닝을 위해 데이터셋을 이용할 때 스케일링이 되지 않은 feature를 그대로 사용하면 유의미한 결과를 얻지 못할 수 있다.
예를 들어 LinearRegression의 상황을 보자. x1은 0 ~ 10의 분포를 갖고 x2는 10000 ~ 100000의 분포를 갖는데 y는 10000 ~ 100000의 분포를 갖는다고 가정해보자. 이 때는 x1이 유의미한 Feature일 수 있음에도 y에 영향을 주지 않는다고 생각할 수 있다. 그렇기 때문에 데이터 스케일링을 통해 분포를 맞춰줘야 하는 상황이 있다.
물론 모든 상황에서 스케일링을 해줘야 하는 것은 아니다. 오히려 스케일링을 하지 않고 원래의 분포를 유지해야 하는 상황도 있다.
StandardScaler()
- 특성들을 평균 : 0, 분산 : 1 을 갖는 정규분포로 스케일링해준다.
- 최솟값과 최댓값에 제한을 두지 않기 때문에 이상치에 민감하다.
- 회귀보다 분류에 유리하다.
MinMaxScaler()
- 최솟값을 0, 최댓값을 1로 설정하고 스케일링해준다.
- 이상치에 민감하다.
- 분류보다 회귀에 유리하다.
MaxAbsScaler()
- [-1, 1] 사이로 값들을 스케일링해준다.
- 데이터가 양수일 때, MinMaxScaler()와 같다.
RobustScaler()
- 평균과 분산 값 대신에 중간값과 사분위수를 이용한다.
- 이상치에 민감하지 않다.
Normalizer()
- 위의 스케일러와 다르게 행 간의 feature값들의 거리를 1로 조정해준다.
- 딥러닝 모델 사용할 때 자주 이용한다.
