👉 들어가기
아직까지는 백준 사이트의 문제분류를 통해서 문제를 찾아 들어가다 보니, DP임을 알고 풀었던 문제입니다.
아직 점화식을 세우는데 익숙하지 않아서 이리저리 고민했었는데, 결국은 동전으로 만들 수 있는 가치의 합을 점화식으로 세우면 해결되는 문제입니다.
✏️ 문제 풀이
이해를 돕기 위해 아이패드를 통해 표를 그려봤습니다! 차근차근 하나씩 말씀드릴테니 천천히 따라와주세요
k 는 동전을 통해서 만들어야 하는 가치이며 이를 표의 첫 번째 행에 넣었습니다.
위에서 말했듯, 우리는 동전으로 만들 수 있는 가치의 합인 k 를 점화식으로 세워야 합니다.
먼저 동전 1만 사용하여 k까지의 가치를 만들어 보겠습니다. (2와 5는 사용하지 않습니다)
1을 만드려면 1짜리 동전 1개만 있으면 되므로 1을 기입하겠습니다.
2를 만드려면 1+1로 1가지 이므로 1을 기입하겠습니다.
3을 만드려면 1+1+1로 1가지 이므로 1을 기입하겠습니다.
첫번째, "1을 만들기 위해서 1 하나만 있으면 된다" 는 결국 dp의 초기값을 설정하는 부분이라고 할 수 있습니다.
2는 결국 1을 만든 경우에 1짜리 동전 하나 추가로 얹은 경우 이므로 dp[2] = dp[1] 이고
3도 마찬가지로 2를 만든 경우에 1짜리 동전 하나만 추가로 얹은 경우 이므로 dp[3] = dp[2] 입니다.
이때 dp[2] = dp[1] 에서의 dp[1]이 초기값이 되는 것 입니다.
이를 일반화 시키면 다음과 같은 식이 될 것 입니다.
dp[k] = dp[k-동전의 가치]
마찬가지로 4~10 까지도 같은 방식으로 표를 채워줍니다.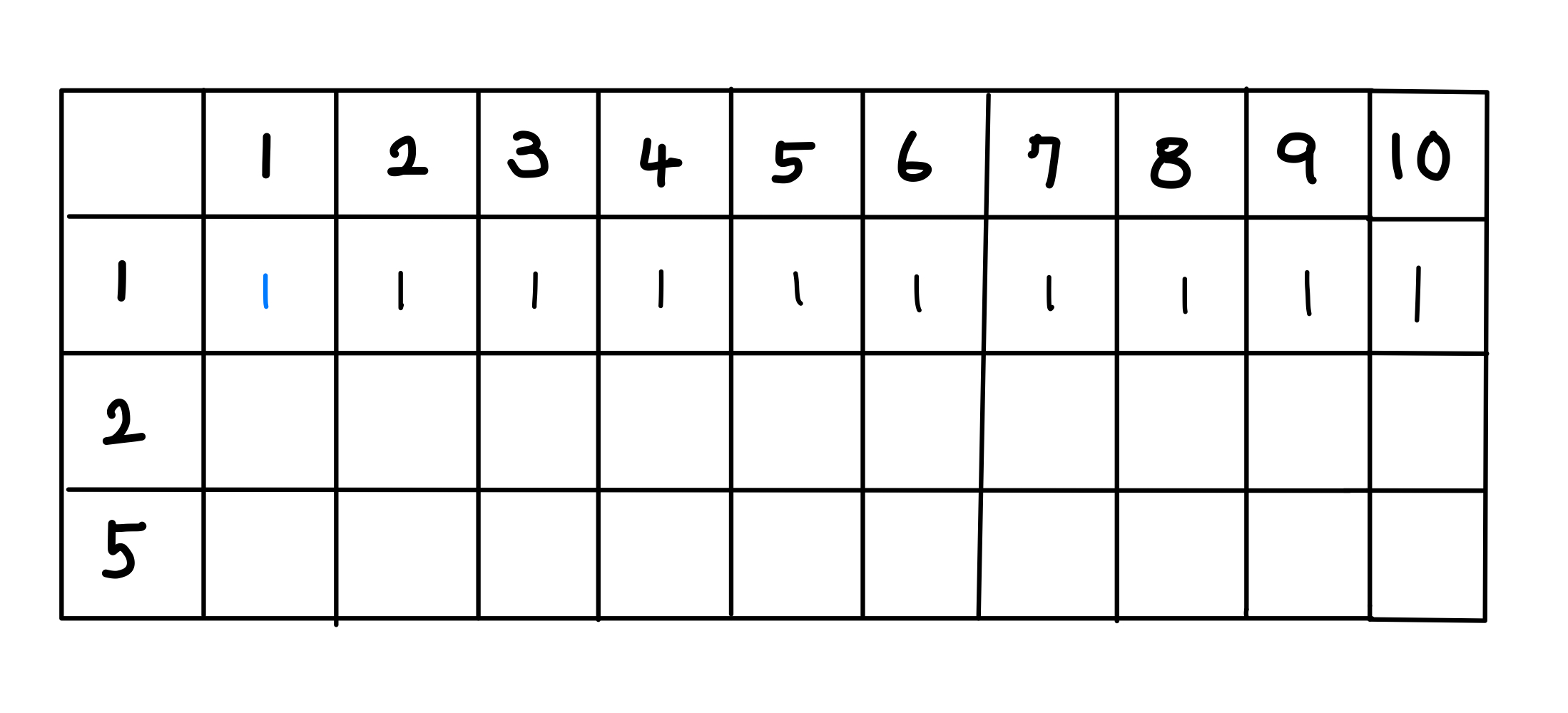
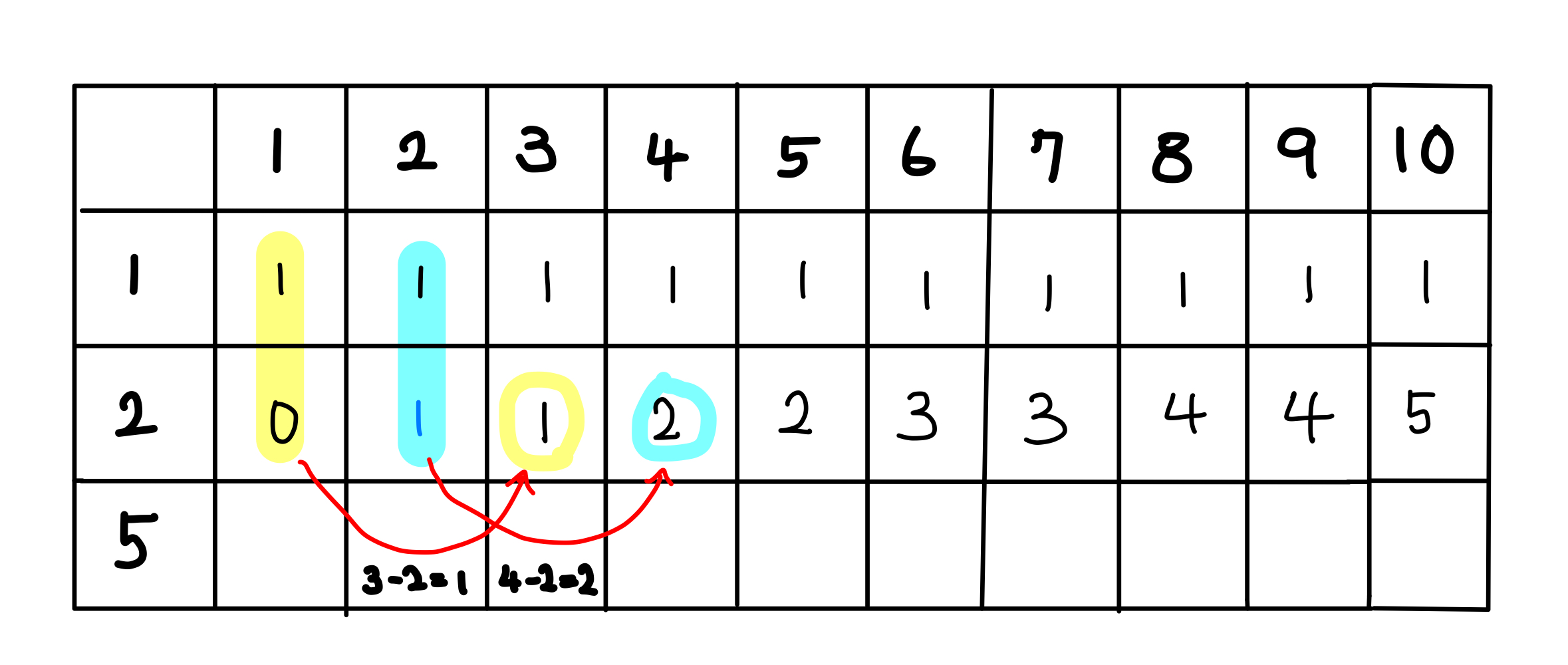
좀 더 핵심적인 부분입니다. 방식은 동일하지만 두 번째 동전을 이용해서 구할 때 부터 좀 더 이해가 수월할 것입니다.
1를 만드려고 했으나, 2짜리 동전으로는 1을 만들 수 없습니다. 0을 기입합니다.
2를 만드려면 2짜리 동전 1개만 있으면 되므로 1을 기입하겠습니다.
3을 만드려면 1을 만드는 방법의 수 (dp[1])에 2짜리 동전 1개가 필요하므로 dp[1] 인 1을 기입합니다.
4를 만드려면 2를 만드는 방법의 수 (dp[2])에 2짜리 동전 1개가 필요하므로 dp[2] 인 2를 기입합니다.
조금 다른 점이라면, 위의 일반화 된 식에다가 동전의 가짓 수가 추가 된 만큼을 더해줘야 합니다.
4를 만드는 과정을 통해 다시 설명드리겠습니다.
4를 만드는 방법은 dp[2] + 2짜리 동전 1개 입니다.
이때 dp[2]는 동전 1을 통해서 구한 값에, 동전 2를 통해서 구한 값을 더한 2가지 경우의 수를 갖고 있기 때문에
이와 같이 점화식을 완성할 수 있습니다.
dp[k] = dp[k] + dp[k-동전의 가치]
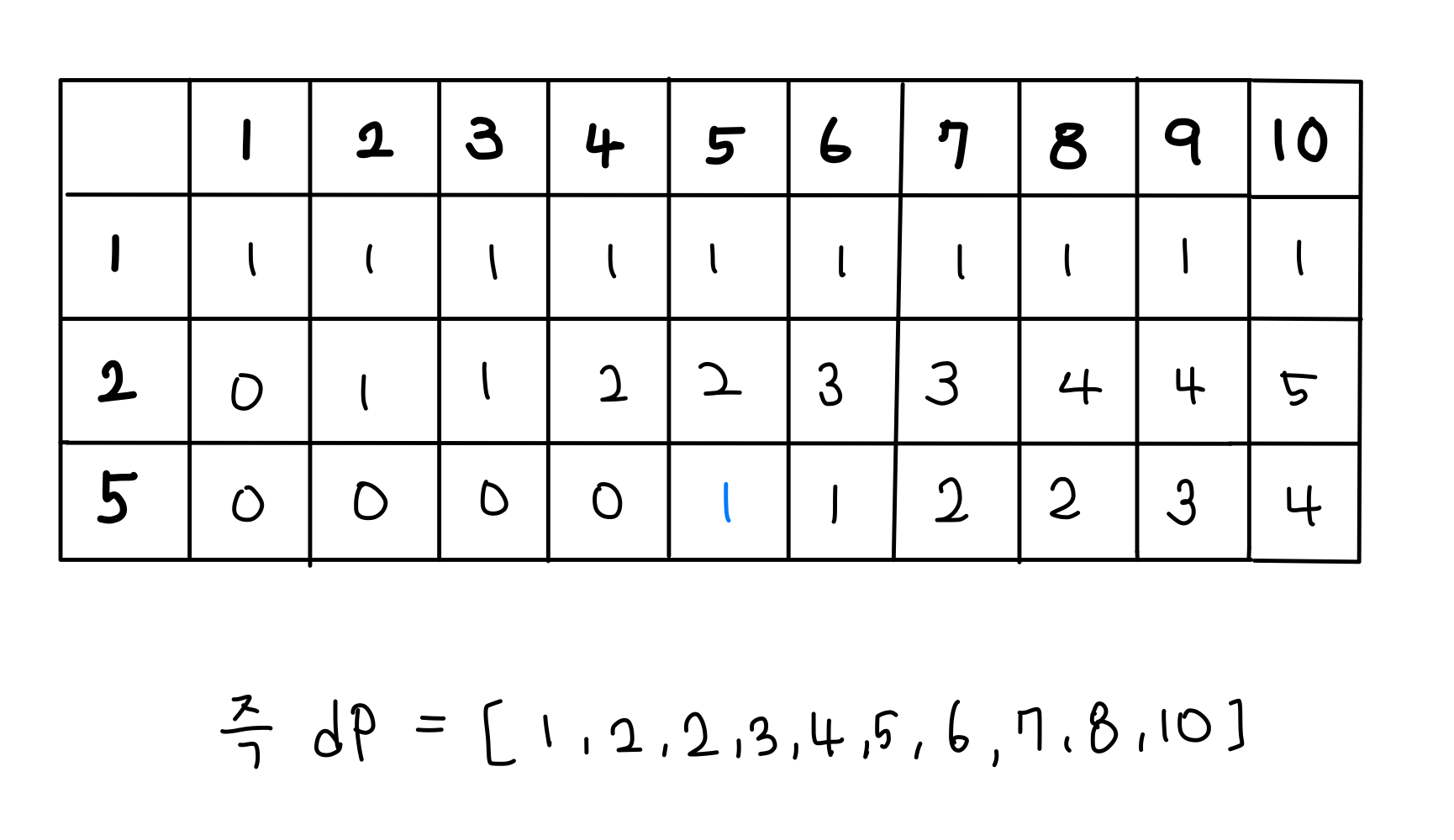
이와 같은 과정을 통해 5짜리 동전을 사용한 경우도 표를 완성한다면, 구하고자 하는 배열을 모두 채울 수 있겠습니다.
from sys import stdin
input = stdin.readline
n, k = map(int, input().split())
dp = [0 for _ in range(k+1)]
coin = [int(input()) for _ in range(n)]
for c in coin:
for i in range(1, k+1):
if(i == c): # 2원을 만들기 위해 2원짜리 동전을 써야하는 경우(2원 1개)
dp[i] += 1
# dp를 활용하기 위함 -> dp[구해야 하는 값 - 코인의 가치] 는 결국 현재 코인을 더해 dp[구해야 하는 값] 과 같다.
elif(i > c):
dp[i] = dp[i] + dp[i-c]
print(dp[k])감사합니다 😁

