여러 개의 큐비트의 상태를 나타내는 방법과, 이러한 큐비트가 서로 어떻게 상호 작용할 수 있는지 학습한다.
다중 큐비트(Multi-Qubits) 상태 표현
단일 비트에는 두 가지 가능한 상태가 있고, 큐비트의 상태에는 두 복소수 값이 있다.
두 비트에는 네 가지 가능한 상태가 있다.
00 01 10 11
두 큐비트의 상태를 표현하기 위해서는 네 개의 복소수 진폭이 필요하다.
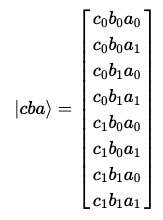
해당 진폭들을 다음과 같이 4차원 벡터에 저장할 수 있다.
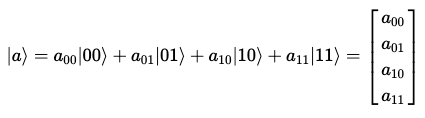
여기서 a는 multi-qubits를 의미하는 문자열(변수)을 나타낸다.
측정 규칙을 동일하게 적용할 수 있다.
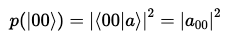
정규화 조건 역시 동일하게 적용된다.
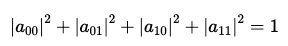
두 개의 분리된 큐비트가 있는 경우, 크로네커 곱(kronecker product, ⊗)을 통해 집합적 상태를 설명할 수 있다.
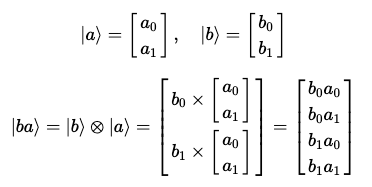
동일한 규칙에 따라, kronecker product를 통해 어떠한 개수의 큐비트라도 집합적 상태를 나타낼 수 있다.
크로네커 곱은, Multi-qubits의 상태를 표현하기 위해(상태 벡터를 생성하기 위해) 사용한다.
얽힘을 표현하기 위함이 아니라, 차원을 표현하기 위한 것이다.
즉, 차원 확장이 목적이다.
// Q. tensor product and kronecker product의 차이는 무엇인가?
n개의 큐비트가 있다면, 2^n개의 복소 진폭(complex amplitudes)을 추척해야 한다.
큐비트 수에 따라 이러한 벡터는 지수적으로 증가하며, 이는 양자 컴퓨터가 많은 수의 큐비트를 시물레이션하기 어려운 이유이다.
아래의 회로를 보자.
qc = QuantumCircuit(3)
# Apply H-gate to each qubit:
for qubit in range(3):
qc.h(qubit)
# See the circuit:
qc.draw()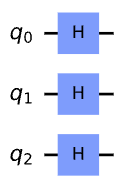
각각의 큐비트는 상태 |+>이다.
따라서, 아래와 같은 벡터로 나타낼 수 있다.
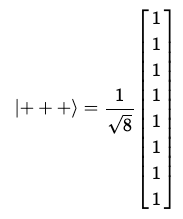
# Let's see the result
svsim = Aer.get_backend('aer_simulator')
qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
# In Jupyter Notebooks we can display this nicely using Latex.
# If not using Jupyter Notebooks you may need to remove the
# array_to_latex function and use print(final_state) instead.
from qiskit.visualization import array_to_latex
array_to_latex(final_state, prefix="\\text{Statevector} = ")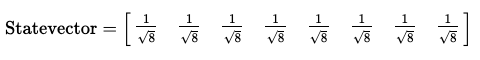
다중-큐비트(Multi-Qubit) 상태 벡터의 단일 큐비트(Single Qubit) 게이트
X 게이트를 행렬로 표현하면 다음과 같다.
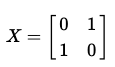
상태 |0>에 대해서 다음과 같이 동작한다.
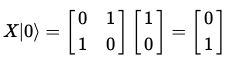
다중 큐비트 벡터에서는 어떻게 동작할까?
크로네커 곱을 사용해서 다중 큐비트 상태 벡터를 연산한 것처럼, 텐서 곱을 사용해서 이러한 상태벡터에 작용하는 행렬들을 계산하면 된다.
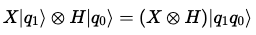
위 수식을 계산하면 다음과 같다.
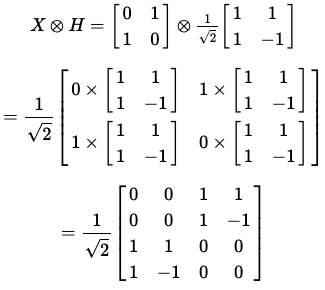
위 수식을 간단하게 나타내면 다음과 같다.
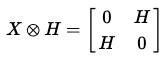
이를 우리의 4차원 상태 벡터인 |q1q0⟩에 적용할 수 있다.
아래와 같이, 멀티 큐비트 회로에서 하나의 큐비트에만 게이트를 적용하려는 경우, 항등 행렬과 함께 크로네커 곱을 사용한다.
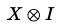
qc = QuantumCircuit(2)
qc.x(1)
qc.draw()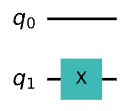
# Simulate the unitary
usim = Aer.get_backend('aer_simulator')
qc.save_unitary()
qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
# Display the results:
array_to_latex(unitary, prefix="\\text{Circuit = } ")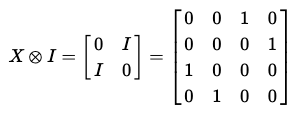
책, 소프트웨어, 논문마다 큐비트의 순서가 다르다(lsb, msb).
따라서, 동일한 회로의 크로네커 곱일지라도 다르게 표현될 수 있음을 염두한다.
다중-큐비트(Multi-Qubit) 게이트
다중 큐비트 벡터의 상태를 나타내는 법, 다중 큐비트 벡터에 단일 큐비트 게이트 적용을 알았으므로, 큐비트가 서로 어떻게 상호작용하는지 학습한다.
The CNOT-Gate
CNOT 게이트는 두 번째 큐비트(타겟)에는 X-gate, 첫 번째 큐비트(제어)에는 |1>의 상태로 동작하는 조건적인 게이트이다.
q0을 제어, q1을 타겟 큐비트로 갖는 CNOT 게이트의 회로도는 다음과 같다.
qc = QuantumCircuit(2)
# Apply CNOT
qc.cx(0,1)
# See the circuit:
qc.draw()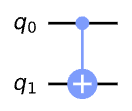
큐비트가 중첩되지 않은 경우(고전 비트처럼), 진리표를 통해 다음과 같이 나타낼 수 있다.
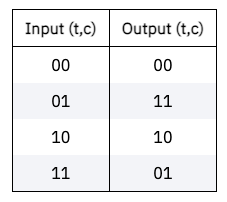
4차원 상태 벡터에서는 다음과 같은 두 행렬 중 하나를 갖는다.
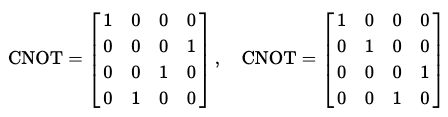
이는 제어, 타겟 큐비트가 어떤 큐비트냐에 따라 다르다.
책, 시뮬레이터, 논문마다 상이하며, Qiskit의 경우 좌측의 행렬이 CNOT 회로이다.
해당 행렬은 우리 상태 벡터의 |01>과 |11>의 진폭을 교환한다.
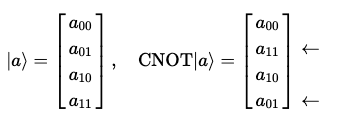
고전 상태에서는 위 진리표대로 작동한다는 것을 알고 있으므로, 중첩된 상태의 큐비트에서 어떻게 작동하는지를 살펴본다.
아래와 같이, 상태 |+>의 큐비트에 적용한다.
qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0)
qc.draw()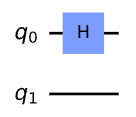
이 때의 상태 벡터는 다음과 같다.
# Let's get the result:
qc.save_statevector()
qobj = assemble(qc)
result = svsim.run(qobj).result()
# Print the statevector neatly:
final_state = result.get_statevector()
array_to_latex(final_state, prefix="\\text{Statevector = }")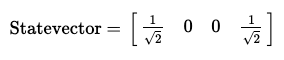
큐비트의 상태는 다음과 같이 나타낼 수 있다.
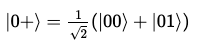
현재는 얽혀있지 않은 상태이다.
왜냐하면 한 비트에 대해 다른 한 비트의 값이 영향을 받지 않기 때문이다.
CNOT 게이트를 적용한다.
qc = QuantumCircuit(2)
# Apply H-gate to the first:
qc.h(0)
# Apply a CNOT:
qc.cx(0,1)
qc.draw()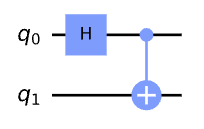
상태 벡터는 아래와 같다.
# Let's get the result:
qc.save_statevector()
qobj = assemble(qc)
result = svsim.run(qobj).result()
# Print the statevector neatly:
final_state = result.get_statevector()
array_to_latex(final_state, prefix="\\text{Statevector = }")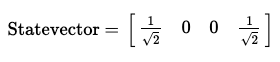
상태는 다음과 같다.
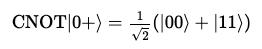
이러한 상태는 얽혀 있다.
때문에, 얽힌 상태라고 한다.
얽힌 상태(Entangled States)
우리는 아래와 같은 상태를 만들었다.
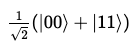
이는 Bell State라고 잘 알려져 있다.
|00>로 측정될 확률이 50%, |11>로 측정될 확률이 50%이다.
|01>과 |10>으로 측정될 확률은 0%이다.
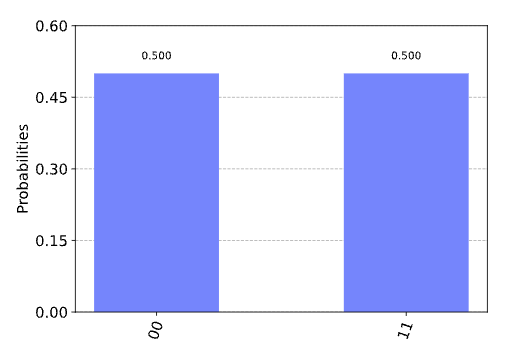
이러한 결합된 상태는 두 개의 분리된 큐비트의 상태로는 만들 수 없다.
큐비트들이 중첩되어 있음에도 불구하고, 하나의 큐비트의 상태를 측정하면 나머지 하나의 상태를 알 수 있으며, 중첩이 붕괴된다.
예를 들어, 최상위 큐비트를 측정하고 |1>의 상태를 얻었다면, 큐비트의 집합적 상태는 다음과 같이 변경된다.
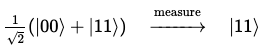
이러한 큐비트들은 심지어 몇 광년 떨어져 있더라도, 하나의 큐비트를 측정할 경우 중첩을 붕괴시키며 나머지에게 즉각적인 영향을 미친다.
이는 spooky action at a distance라 한다.
측정의 결과는 무작위이며, 한 큐비트의 측정 통계는 다른 큐비트의 작업에 어떠한 영향도 받지 않는다는 점에 유의해야 한다.
이러한 이유 때문에, 공유 양자 상태를 통해 통신할 방법이 없다.
이는 no-communication theorem으로 알려져 있다.
얽힌 상태의 시각화
앞전에, 얽힌 상태를 개별 큐비트의 상태로 나타낼 수 없다고 하였다.
이는 별도의 블로흐 구에 상태를 플로팅하려고 하면 정보를 잃게 될 것임을 의미한다.
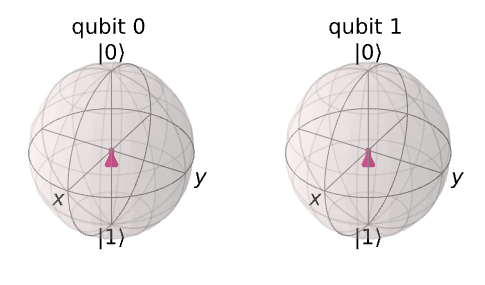
앞전 챕터에서의 블로흐 구에 대한 정의를 고려할 때, Qiskit이 이러한 얽힌 큐비트를 블로흐 벡터로 계산하는 방식이 명확하지 않을 수 있다.
단일-큐비트의 경우, 축을 따라 블로흐 벡터의 위치는 해당 기저에서 측정하는 기대값과 일치한다.
이를 블로흐 벡터를 플로팅 하는 규칙으로 삼으면, 위의 결론에 도달한다.
이는 특정 측정이 보장되는 단일-큐비트 측정 기저가 없음을 보여준다.
이는, 항상 단일-큐비트 기저를 설정할 수 있는 단일 큐비트 상태와 대조된다.
이렇게 개별적으로 큐비트를 보면, 우리는 큐비트 사이 상관 관계의 중요한 효과를 놓치게 된다.
우리는 얽힌 상태의 차이를 구별할 수 없게 된다.
예를 들어, 아래의 두 얽힌 상태를 보자.
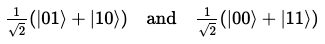
CNOT|1+>과 CNOT|0+>이다.
위의 두 상태는 측정 결과가 매우 다른 상태임에도 불구하고, 개별 블로흐 구에서는 동일하게 보인다.
이러한 상태 벡터를 어떻게 시각화 할 수 있을까?
이 상태 벡터는 4개의 진폭(복소수)을 가진 간단한 집합이며, 이를 이미지에 매핑할 수 있는 방법은 무궁무진하다.
그 중 하나인, Q-sphere에 대해 살펴본다.
Q-sphere에서, 각 진폭은 구 표면의 blob으로 표현된다.
Blob의 크기는 진폭의 크기에 비례하며, 색상은 진폭의 위상에 비례한다.
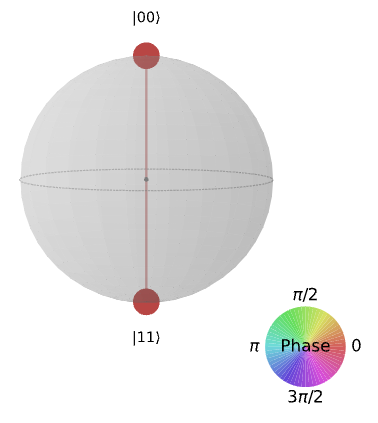
CNOT|0+>을 위와 같이 표현할 수 있다.
위의 의미는, |00>과 |11>의 진폭은 동일하며, 나머지 진폭은 0라는 의미이다.
이를 통해 큐비트 간의 상관관계를 명확하게 볼 수 있다.
Q-구의 모양은 중요하지 않으며, 단순하게 blob을 배열하기에 좋은 방법이다.
상태에 있는 0의 개수는 Z축의 상태들의 위치에 비례하므로, 우리는 구의 상단 극점에서 진폭 |00>을 볼 수 있으며, 구의 하단 극점에서 진폭 |11>을 볼 수 있다.
Phase Kickback
앞전에, CNOT 게이트를 사용하여, control 큐비트의 상태를 |+>에 둠으로써 두 개의 큐비트를 얽히게 할 수 있음을 알았다.
두 번째(target) 큐비트 역시 중첩 상태에 두면 어떻게 될까?
qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.cx(0,1)
display(qc.draw()) # `display` is a command for Jupyter notebooks
# similar to `print`, but for rich content
# Let's see the result
svsim = Aer.get_backend('aer_simulator')
qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
display(array_to_latex(final_state, prefix="\\text{Statevector} = "))
plot_bloch_multivector(final_state)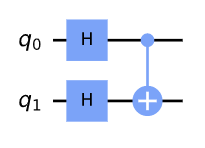
위의 회로에서, 아래의 상태에 대해 CNOT이 작동한다.
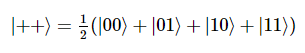
CNOT이 진폭 |01>과 |11>을 교환하기 때문에, CNOT 적용 후에도 변화가 없는 것을 확인할 수 있다.
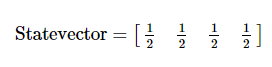
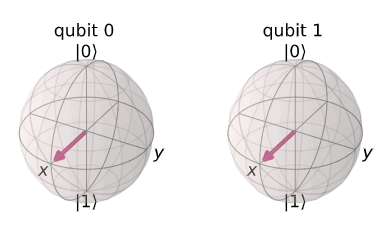
타겟 큐비트를 상태 |->에 놓는다.
따라서, 음의 위상을 갖는다.
qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
qc.h(1)
qc.draw()
# See the result
qc1 = qc.copy()
qc1.save_statevector()
final_state = svsim.run(qc1).result().get_statevector()
display(array_to_latex(final_state, prefix="\\text{Statevector} = "))
plot_bloch_multivector(final_state)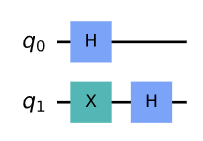
따라서, 아래의 상태를 형성한다.
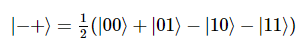
상태 벡터는 아래와 같다.
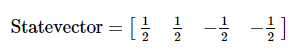
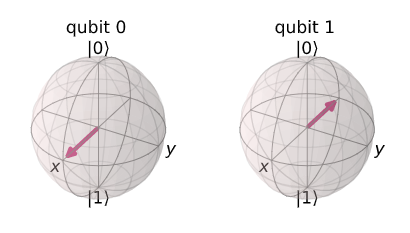
해당 상태에 대해 CNOT 게이트를 적용시킨다.
진폭 |01>과 |10>을 교환함으로써 수행한다.
결과 상태는 다음과 같다.
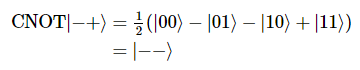
위 상태는 target 큐비트의 상태를 변화시키지 않은 상태를 유지(|-> 유지)하면서, control 큐비트의 상태에 영향을 끼친다(|+> -> |->).
qc.cx(0,1)
display(qc.draw())
qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
display(array_to_latex(final_state, prefix="\\text{Statevector} = "))
plot_bloch_multivector(final_state)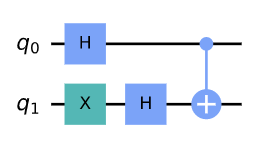
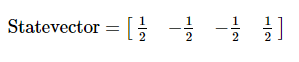
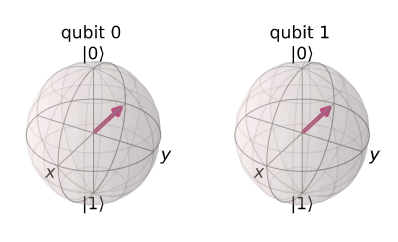
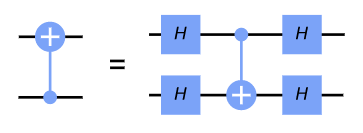
H 게이트는 |+>를 |0>으로, |->를 |1>로 변환시킨다.
CNOT 게이트를 H 게이트들로 감쌈을 통해, CNOT 게이트가 반대 방향으로 적용되는 것과 동일한 행동을 수행하는 것을 알 수 있다.
qc = QuantumCircuit(2)
qc.h(0)
qc.h(1)
qc.cx(0,1)
qc.h(0)
qc.h(1)
display(qc.draw())
qc.save_unitary()
usim = Aer.get_backend('aer_simulator')
qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
array_to_latex(unitary, prefix="\\text{Circuit = }\n")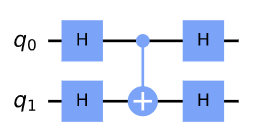
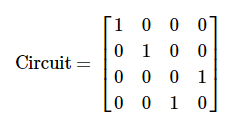
It equals
qc = QuantumCircuit(2)
qc.cx(1,0)
display(qc.draw())
qc.save_unitary()
qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
array_to_latex(unitary, prefix="\\text{Circuit = }\n")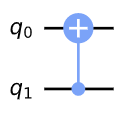
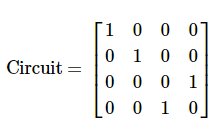
이는 위상 반동(phase kickback)의 예시 이다.
위상 반동(Phase kickback)
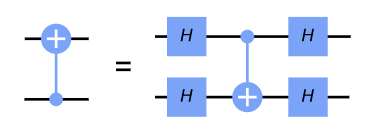
앞에서 위가 성립함을 알 수 있었다.
이는 반동(위상 반동, phase kickback)의 예시이며, 위상 반동은 매우 중요하며 양자 알고리즘에서 널리 사용된다.
반동(kickback)이란, 게이트에 의해 큐비트에 추가된 고유값(eigenvalue)이 제어된 연산을 통해 다른 큐비트에 '반동(kicked back)'을 일으키는 것을 의미한다.
예를 들어, 큐비트 |->에 X 게이트를 적용하면 위상이 -1이 된다.
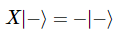
(∣−⟩을 target 큐비트로 하는 CNOT 게이트에서)
control 큐비트가 ∣0⟩ 또는 ∣1⟩일 때, 이 위상은 전체 상태에 영향을 주지만, 이것은 전역 위상이기 때문에 관찰 가능한 효과는 없다.
// 전역 위상만 다른 상태들은 물리적으로 구분되지 않는다.
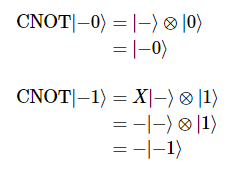
흥미로운 점은, Control 큐비트가 중첩 상태일 때, |1> 방향의 control 큐비트의 구성요소가 해당 target 큐비트의 위상 계수(phase factor)에 영향을 끼치며, 이렇게 적용된 위상 계수는 control 큐비트의 상대 위상에 변화를 준다는 것이다.
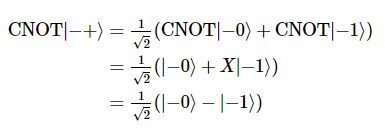
이는 다음과 같이 분리된 두 개의 큐비트 상태로 나타낼 수 있다.
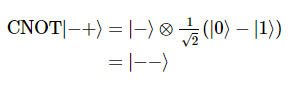
CNOT 게이트를 H 게이트로 감싸는 것은 큐비트의 기저를 계산 기저(∣0⟩, ∣1⟩)에서 (∣+⟩, ∣−⟩)으로 변환한다.
어떤 하드웨어는 한 방향으로의 CNOT만 허용하는데, 이 변환 특성을 통해 CNOT을 양 방향 모두 가능하게 할 수 있어 유용하다.
T-게이트를 사용한 반동
CNOT 게이트 이외에도, controlled 되는 연산인 controlled-T 게이트가 있다.
T-게이트의 행렬은 다음과 같다.
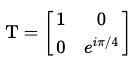
Controlled-T 게이트는 다음과 같다.
qc = QuantumCircuit(2)
qc.cp(pi/4, 0, 1)
display(qc.draw())
# See Results:
qc.save_unitary()
qobj = assemble(qc)
unitary = usim.run(qobj).result().get_unitary()
array_to_latex(unitary, prefix="\\text{Controlled-T} = \n")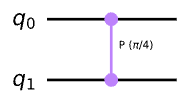
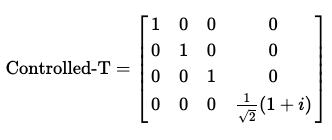
Controlled-T 게이트의 행렬은 다음과 같이 나타낼 수 있다.
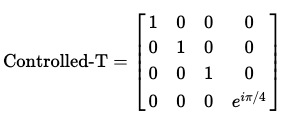
보다 일반적으로, 다음의 규칙을 적용하여 어떠한 controlled-U 연산에 대한 행렬을 찾을 수 있다.
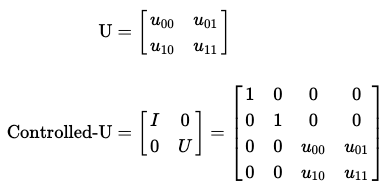
혹은, Qiskit의 큐비트 순서를 사용한다면 다음과 같이 나타낼 수 있다.
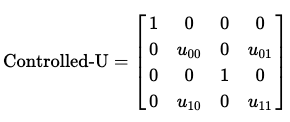
상태 |1>의 큐비트에 T-게이트를 적용한다면, 해당 큐비트에 e^(iπ/4)의 위상을 추가한다.
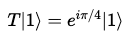
이는 전역 위상이므로 관찰할 수 없다.
그러나, |+> 상태의 다른 큐비트를 사용하여 이러한 연산을 제어한다면, 위상은 더이상 전역적이지 않고 상대적이게 되며, 제어(control) 큐비트의 상대적 위상을 변경한다.
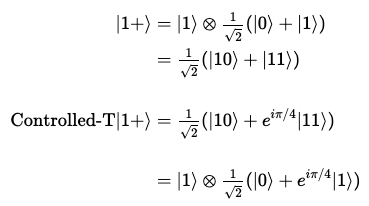
이는 target 큐비트를 변화시키지 않으면서, control 큐비트를 블로후 구 상에서 Z-축으로 회전시키는 효과가 있다.
qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
display(qc.draw())
# See Results:
qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
plot_bloch_multivector(final_state)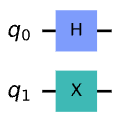
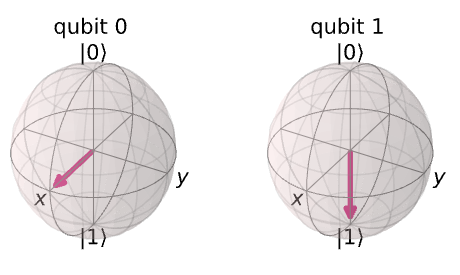
qc = QuantumCircuit(2)
qc.h(0)
qc.x(1)
# Add Controlled-T
qc.cp(pi/4, 0, 1)
display(qc.draw())
# See Results:
qc.save_statevector()
qobj = assemble(qc)
final_state = svsim.run(qobj).result().get_statevector()
plot_bloch_multivector(final_state)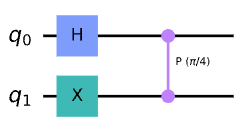
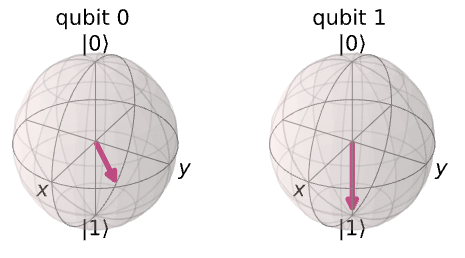
위의 코드 실습에서, 가장 좌측 큐비트가 블로흐 구 상에서 Z-축으로 π/4만큼 회전된 것을 확인할 수 있다.
정확히는, controlled-T-게이트로 연결된 두 큐비트 모두 회전한 것이다.
이를 통해, Qiskit이 controlled-Z-rotation 게이트를 대칭적으로(제어와 타겟 대신 두 개의 제어) 표현하는지를 알 수 있다.
모든 경우에, 명확한 제어와 타겟 큐비트가 없기 때문이다.
More Circuit Identities
// 추후 계속
