Deutsch-Jozsa(도위치-조사) 알고리즘
Deutsch-Jozsa 알고리즘은, 고전 알고리즘보다 뛰어난 성능을 보인 최초의 양자 알고리즘이다.
특정 문제에 대한 계산 도구로 양자 컴퓨터를 사용하는 것이 이점이 있다는 것을 보여주었다.
Deutsch-Jozsa Problem
입력으로 비트 문자열(n개의 비트)을 받고, 0 혹은 1을 반환하는 미지의(hidden) 불리언(Boolean) 함수 가 있다.
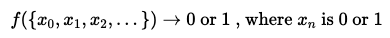
주어진 불리언 함수의 특성은, 균형함수이거나 상수함수여야 한다.
상수 함수는 모든 입력에 대해 0이나 1을 반환하는 반면, 균형 함수는 모든 입력의 절반에 대해 0을 반환, 나머지 절반에 대해 1을 반환한다.
주어진 미지의 함수 가 균형(balanced)인지, 상수(constant)인지를 확인하는 것이 우리의 임무이다.
Deutsch-Jozsa 문제는 단일 비트 Deutsch 문제의 -비트 확장, 일반화이다.
The Classical Solution
Quantum Solution의 효율성을 증명하기 위해서는 먼저 해당 문제의 classical solution에 대해 알아야 한다.
고전적인 방식은 다음과 같다.
최상의 경우, 오라클(oracle)에 대한 두 개의 쿼리(query)만으로 해당 부울 함수()가 균형을 이루는지를 확인할 수 있다.
예를 들어, and 을 얻는다면, 두 개의 다른 출력을 얻었으므로 해당 함수가 균형을 이루는 것을 알 수 있다.
최악의 경우, 시도하는 모든 입력에 대해 동일한 출력이 나온다면, 가 상수함수인지 균형함수인지 확인하기 위해, 가능한 모든 입력의 절반을 시도한 후, 추가적으로 1회를 더 시도해야 확신할 수 있다.
이 경우에, 가능한 입력의 전체 개수가 개라면, 개의 입력을 시도해야 한다.
예를 들어, 4-비트 문자열이 있을 때 가능한 16개의 전체 조합에서 8개를 체크하여 출력으로 모두 0이 나왔다 할 지라도, 9번째 입력이 1을 반환하여 가 균형함수가 될 가능성이 있다.
// 이 아래는 굳이?
확률적으로, 이것은 매우 희박하다.
사실, 연속적으로 같은 결과를 얻는다면, k번째를 입력할 때 해당 함수가 상수함수일 확률을 다음과 같이 나타낼 수 있다.
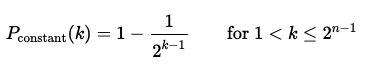
현실적으로, 이상의 결과를 확신할 수 있다면, 조기에 고전 알고리즘을 종료할 수 있다.
허나 의 확신을 위해서는, 의 입력값을 체크해야 한다.
Deutsch-Jozsa Algorithm (Quantum Solution)
양자 컴퓨터를 사용하여 개선한 방식은 다음과 같다.
상태 를 로 매핑하는 양자 오라클로 구현된 함수 가 있는 경우, 함수 를 한 번 호출하는것 만으로 이 문제를 100%의 신뢰도로 문제를 해결할 수 있다.
여기서, ⊕는 모듈러-2 덧셈(xor 게이트, addition modulo 2) 연산이다.
Deutsch-Jozsa 알고리즘의 일반적인 회로이다.
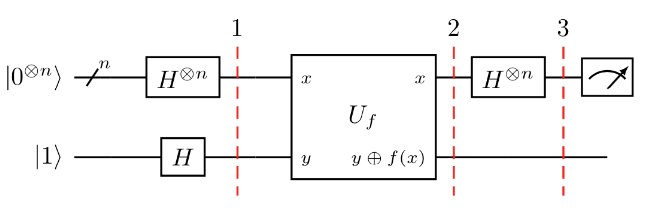
알고리즘 단계는 다음과 같다.
-
두 개의 양자 레지스터를 준비한다.
첫 번째는 |0>으로 초기화된 -qubit 레지스터이며, 두 번째는 |1>로 초기화된 한개의 큐비트 레지스터이다.
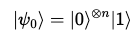
-
각각의 큐비트에 하다마드 게이트를 적용한다.
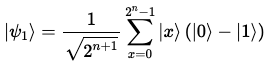
-
를 로 변환하는 양자 오라클을 적용한다.
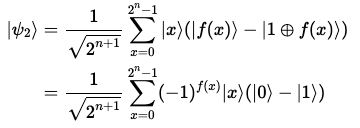
각각의 에 대해, 는 0 또는 1이다. -
이 때, 두 번째 단일 큐비트 레지스터가 무시될 것이다.
첫 번째 레지스터의 각각의 큐비트에 하다마드 게이트를 적용한다.
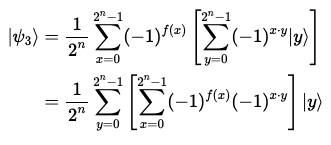
은 비트 곱의 합이다. -
첫 번째 레지스터를 측정한다.
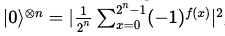
Constant라면, 첫 번째 레지스터의 큐비트들의 상태에 대해 변화가 없었으므로, n개의 모든 큐비트가 초기 상태와 동일하게 |0> 상태로 관측될 것이다.
따라서, 초기 상태인 |0> 상태의 n개의 큐비트들을 측정할 확률은 1이다.
Balanced라면, 유니타리 f의 phase kickback에 의해서 큐비트들의 상태에 변화가 가해졌으므로, |0> 상태가 아닌 큐비트가 반드시 한 개 이상 관측될 것이다.
따라서, |0> 상태의 큐비트들을 측정할 확률은 0이다.
Why Dose This Work?
Constant Oracle
오라클이 상수(constant)라면, 입력 큐비트들에 대해 어떠한 영향도 없을 것(전역 위상만 변함)이다.
그러므로, 쿼리 전과 후의 양자 상태는 동일할 것이다.
H-게이트와 그의 역행렬(inverse)가 동일하므로, 2번 단계에서 하다마드 게이트를 적용하여 변경하였던 양자 상태를, 4번 단계에서 다시 하다마드 게이트를 적용하여, 첫 번째 레지스터의 초기 양자 상태인 |00...0>을 복구할 것이다.
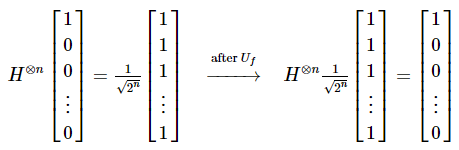
Balanced Oracle
2단계 이후, 입력 레지스터는 계산 기저의 모든 상태에 대해 동일한 중첩을 유지하고 있을 것이다.
오라클이 균형(balanced)이라면, 위상 반동(phase kickback)에 의해 해당 상태들의 정확히 절반에 대해 음의 위상이 더해질 것이다.
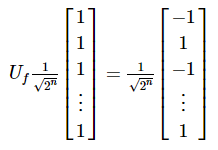
오라클을 쿼리한 이후의 양자 상태는 오라클을 쿼리하기 전의 양자 상태와 직교할 것이다.
따라서, 4단계에서 H-게이트를 적용할 때, |00...0>에 대해 직교하는 양자 상태로 끝날 것이다.
이는 모두 0인 상태(all-zero state)를 절대 측정할 수 없음을 의미한다.
