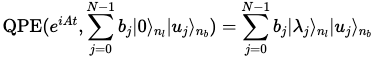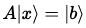선형 시스템의 방정식은 과학, 공학, 탐구 등 많은 분야에 존재한다.
따라서, 행렬을 효율적으로 조작하는 것은 큰 관심사이다.
행렬을 조작하는 대부분의 고전적인 방식은 동작에 다항(polynomial) 시간이 걸린다.
데이터 분석(data analysis)이 점점 강력해짐에 따라, 이러한 행렬의 크기는 동작에 소요되는 다항 시간을 지나치게 길게 만든다.
The HHL algorithm
Introductiopn
HHL 알고리즘은 선형 방정식의 솔루션 벡터의 근사치를 계산하여 문제를 해결한다.
Conditions
주어진 선형 시스템은 낮은 조건수(low condition number) 를 가져야 하며, 행렬 는 -sparse(성긴 행렬)이어야 한다.
이는 가 행 또는 열당 최대 개의 0이 아닌(non-zero) 항목을 가져야 함을 의미한다.
고전 컴퓨터에서, 켤레 기울기(conjugate gradient) 방식 크기 의 -sparse 시스템을 해결하는 것은 의 동작 시간을 요구한다.
여기서, 는 근사치(approximation)의 정확도를 나타낸다.
해당 알고리즘의 사용자는 솔루션 벡터(solution vector) 자체의 값 대신 솔루션 벡터에 대한 스칼라 관측(measurement)에 관심이 있다고 가정한다.
그래서, 사용자는 의 값 자체에는 관심이 없으며, 오히려 에 특정 연산자 을 적용한 에 관심이 있다고 가정할 수 있다.
따라서, 고전 알고리즘이 전체 해답을 반환할 때, HHL은 솔루션 벡터의 근사 함수만을 반환할 수 있다.
또한, 데이터 로드, 해밀턴 시뮬레이션(hamiltonian simulation)과 결과 함수를 계산할 수 있는 효율적인 오라클의 가정 하에, 행렬 는 유니타리 연산자로 변환될 수 있는 에르미트 행렬이어야 한다.
Significance in Machine Learning
추후
Some mathematical background
양자 컴퓨터로 선형 방정식 시스템을 해결하기 위한 첫 번째 단계는 문제를 양자 언어로 인코딩하는 것이다.
시스템을 리스케일링함으로써, 우리는 와 를 정규화하여 각각 양자 상태 와 로 매핑할 수 있다.
대개 이러한 매핑은 (resp. )의 번째 컴포넌트가 양자 상태 (resp. )의 번째 기저 상태의 진폭과 일치한다는 것에 사용된다.
리스케일링한 문제는 다음과 같다.
가 에르미트 행렬(Hermitian)이므로, spectral decomposition을 가진다.
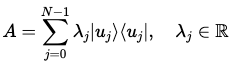
는 각각의 고유값 을 갖는 의 (j번째) 고유 벡터이다.
이는 고유값으로 스케일링된 고유 벡터의 외적의 합으로 적을 수 있다.
그러므로, A의 역을 다음과 같이 나타낼 수 있다.
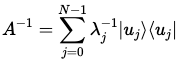
A가 가역행렬이며 에르미트 행렬일 때, 고유 벡터의 직교 기저를 가져야만 한다.
따라서, 의 고유 기저에 다음과 같이 를 쓸 수 있다.
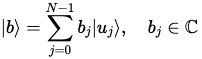
HHL의 목표는 다음의 상태에 있는 판독 레지스터로 알고리즘을 종료하는 것이다.
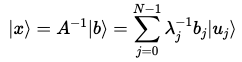
양자 상태에 대해 말하고 있으므로, 이미 암시적인 정규화 상수를 가지고 있다.
Description of the HHL algorithm
HHL 알고리즘은 으로 초기화된 3개의 양자 레지스터를 사용한다.
첫 번째 레지스터는 로 나타낸다.
해당 레지스터는 의 고유값의 이진 표현을 저장하기 위해 사용된다.
두 번째 레지스터는 로 나타내며, 해당 레지스터는 벡터 결과(vector solution)를 포함한다.
또한, 이라 한다.
나머지 레지스터는 보조 큐비트의 역할을 한다.
이들은 개별적 계산에서 중간 단계에 사용되는 큐비트들이지만, 각 계산의 처음에는 으로 세팅되고 각 계산의 마지막에는 의 상태를 복원하기 때문에 이후의 설명에서는 무시될 것이다.
HHL 알고리즘의 고수준 회로도는 다음과 같다.
단순화를 위해, 이후에 일어나는 모든 계산들은 정확하다고 가정한다.
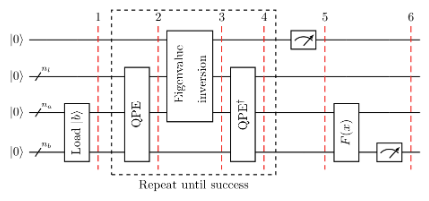
-
데이터 를 로드한다.
다음과 같이 변환이 수행된다.
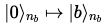
-
다음의 Quantum Phase Estimation(QPE)를 적용한다.
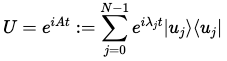
의 고유 기저로 표현되는 레지스터의 양자 상태는 다음과 같아진다.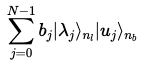
는 의 -bit 이진 표현이다. -
보조 큐비트를 더하고, 조건 의 회전을 적용한다.

는 정규화 상수이다.
또한 위에서 표현된 것처럼, 의 크기는 최소 고유값 보다 작아야 한다.
즉, 이다. -
를 적용한다. 발생할 수 있는 QPE의 에러들을 무시할 경우, 결과는 다음과 같다.
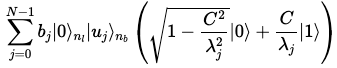
-
보조 큐비트를 계산 기저로 측정한다.
결과값이 1일 경우, 해당 레지스터의 다음과 같은 측정 후 상태에 있다.
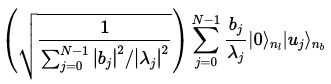
정규화 요소는 결과와 일치한다. -
을 계산하기 위해 관측 가능한 을 적용한다.
Quantum Phase Estimation (QPE) within HHL
QPE는 HHL 알고리즘의 핵심이다.
QPE는 고유 벡터 와 고유값 와 함께 유니타리 가 주어졌을 때, 를 찾기 위한 양자 알고리즘이다.
Definition
가 유니타리이며, 가 각 고유값 의 하나의 고유벡터라고 하자.
양자 위상 추정(QPE) 알고리즘은, 를 위한 유니타리 게이트와 를 입력으로 사용하며, 상태 를 반환한다.
는 에 대한 이진 근사치를 나타내며, 아래 첨자 은 자릿수로 잘림을 나타낸다.
이다.
HHL에서는 인 QPE가 사용된다.
는 우리가 해결하고자 하는 시스템과 연관된 행렬이다.
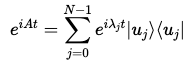
그리고, 고유값 을 갖는 고유 벡터 에 대해, QPE는 결과값 을 낼 것이다.
는 의 -비트 이진 추정치를 나타낸다.
그러므로, 각 는 비트로 정확하게 나타낼 수 있다.