[양자컴퓨터] Simon's Algorithm

Simon's Problem

내용을 알 수 없는(블랙박스) 함수 $f$가 있다.
해당 함수는 일대일(one-to-one, 1:1)이거나 이대일(two-to-one, 2:1)이다.

• 일대일(one-to-one) 함수: 모든 입력에 대해 각각 특정한 하나의 출력이 대응된다.
  

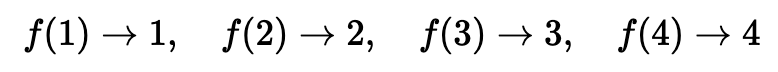
• 이대일(two-to-one) 함수: 두 개의 입력에 대해 특정한 하나의 출력이 대응된다.
  

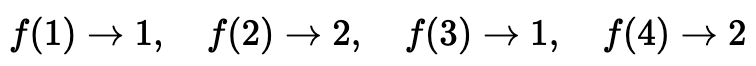
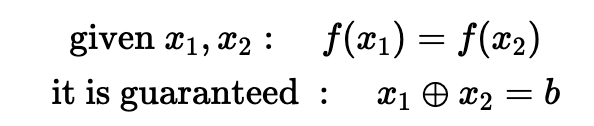
해당 이대일(2:1) 매핑은 미지의 비트열 $b$에 따른 것이다.

$if,$ $y = x ⊕ b$,
$f(x) = f(y)$ 이다.

블랙박스 $f$가 주어졌을 때, $f$가 일대일 함수인지, 이대일 함수인지 얼마나 빠르게 판단할 수 있을까?
만약, 이대일 함수라면 얼마나 빠르게 $b$를 구할 수 있을까?

결과적으로, 두 경우 모두 비트열 $b$를 찾는 문제로 귀결된다.
여기서 $b = 000...$ 는 일대일함수 $f$를 나타낸다.

Classical Soltion

고전적으로,
$b$가 100% $f$에 의해 주어질 때, $b$를 알기 위해서는 $2^{n-1}+1$개의 입력을 체크해야 한다. ($n$은 입력 비트들의 개수)

이는, 동일한 출력의 두 경우를 찾을 때 까지 가능한 입력의 절반 이상을 체크해야 함을 의미한다.

Deutsch-Jozsa 문제와 비슷하게, 최선의 경우 두 번의 시도만으로 문제를 해결할 수 있다.
그러나, $f$가 일대일 함수이거나, 이대일 함수에서 최악의 경우에는, $2^{n-1}+1$번의 시도를 해야 한다.

해당 알고리즘은 $Ω(2^{n/2})$의 하한이나, 일반적으로 시간복잡도는 $n$의 지수적으로 증가한다.

Simon's Algorithm ( Quantum Solution)

사이먼 알고리즘의 양자 회로는 아래와 같다.

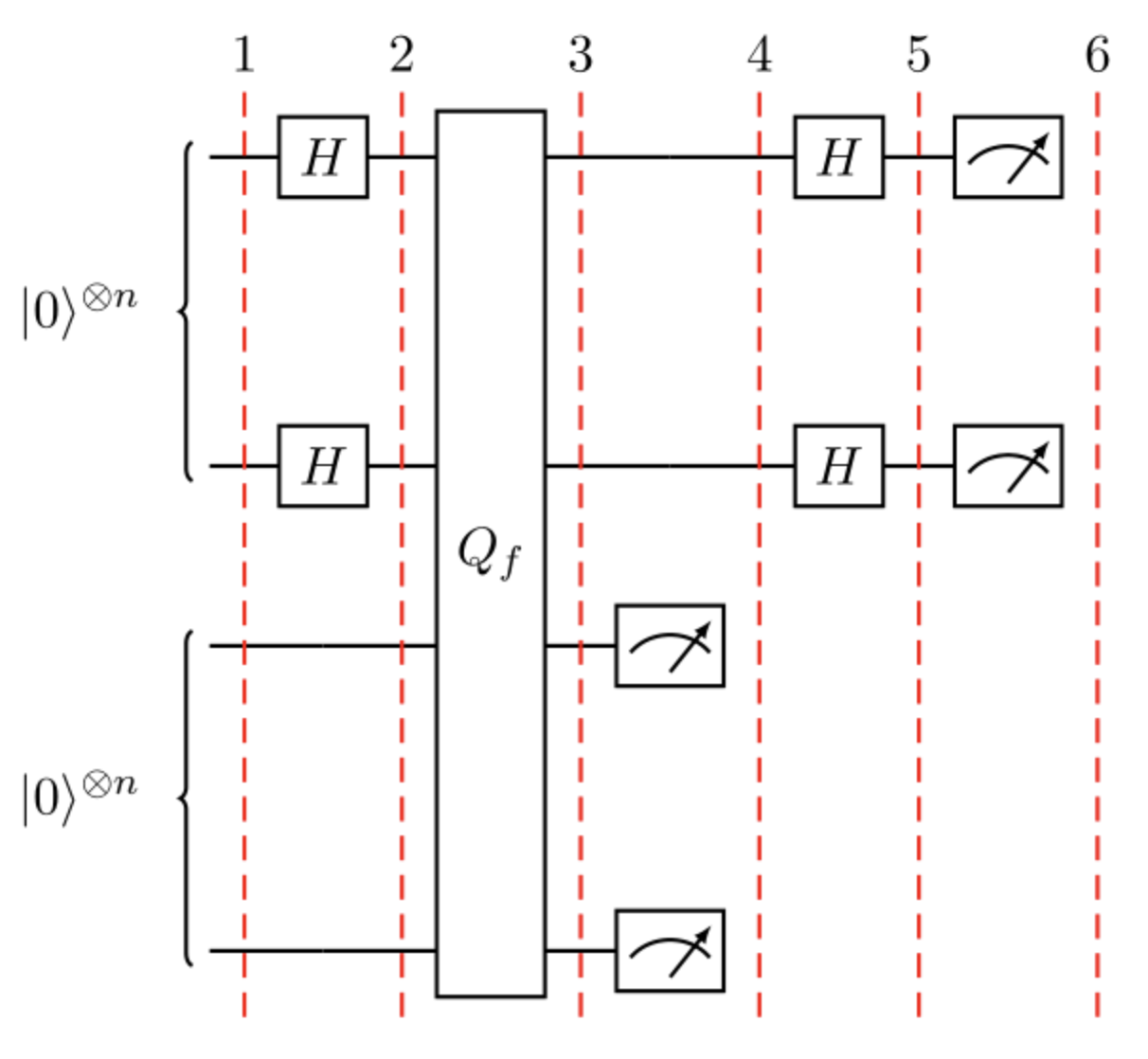
쿼리 함수 $Q_f$는, 두 양자 레지스터에서 다음과 같이 작동한다.

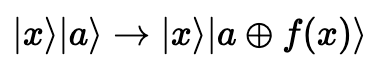
두 번째 레지스터가 $|0〉 = |00...0〉$ 상태에 있는 특별한 경우,

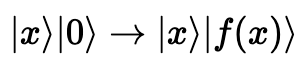
와 같이 나타낼 수 있다.

알고리즘의 순서는 다음과 같다.

1. 두개의 $n$-큐비트 입력 레지스터들을 $|0〉$으로 초기화한다.
   

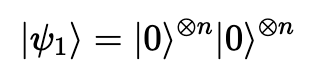
2. 첫 번째 레지스터에 하다마드 게이트를 적용한다.
   

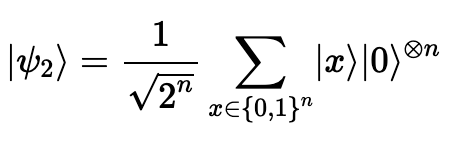
3. $Q_f$를 적용한다.
   

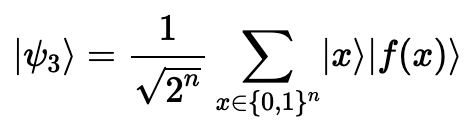
4. 두 번째 레지스터를 측정한다.
   $f(x)$의 값이 관측될 것이다.
   문제의 설정 때문에, 관측값 $f(x)$는 두 가능한 입력인 $x$ 와 $y = x ⊕ b$에 대응된다.
   그러므로, 첫 번째 레지스터는 다음과 같이 변한다.
   
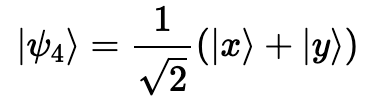
   ( 두 번째 레지스터는 측정하였으므로 생략 )

5. 첫 번째 레지스터에 하다마드 게이트를 적용한다.
   

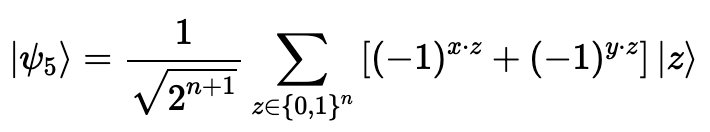
6. 첫 번째 레지스터를 측정하면 특정한 문자열 $z$를 얻을 수 있다.
   문자열 $z$는 아래를 반드시 만족한다.
   
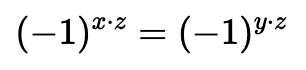
   따라서, 위의 수식을 통해 아래를 도출할 수 있다.
   
   위의 수식을 통해, 측정된 문자열 $z$는 $b$와 내적하면 0이 된다는 것을 알 수 있다.
   따라서, 해당 알고리즘을 대략 $n$번 반복하면 우리는 $z$에 대한 $n$개의 별개의 값을 얻을 수 있으며, 다음과 같은 방정식을 만들 수 있다.
   
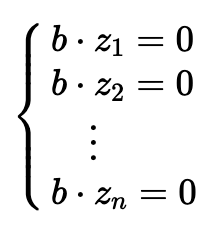
   위 연립방정식으로부터, $b$를 도출해낼 수 있다.

해당 양자 알고리즘은 고전적인 알고리즘보다 지수적으로 적은 단계를 수행한다.
Shor's Algorithm에 영감을 주었으며, 특수한 상황을 해결하는 데 고전적인 시스템보다 기하급수적인 속도 상승을 보여준 첫 번째 양자 시스템이다.