바킹독 0x10 강 - 다이나믹 프로그래밍

📚 동적 계획법(Dynamic Programing)이란?

• 여러 개의 하위 문제를 먼제 푼 후 그 결과를 쌓아올려 주어진 문제를 해결하는 방법.

DP를 사용하면 중간 과정의 중복을 없앨 수 있어 극적인 시간 차이가 발생할 수 있다.

피보나치 예시

• 재귀만 사용했을 경우

public static int fibo(int n){
	if (n<-) return 1;
	return fibo(n-1) + fibo(n-2);
}

이미 진행한 트리에 대해 다시한번 계산을 진행하기에 시간 복잡도가 배로 올라간다.

• DP를 사용했을 경우.

public static int fibo(int n){
	int[] dp = new int[20];
	dp[0] = 1;
	dp[1] = 1;
	for(int i = 2 ; i <= n; i++{
		dp[i] = dp[i-1] + dp[i-2];
	}
	return dp[n];
}

이미 배열을 만들어놓은 경우 계산이 중복되지 않아 O(n) 의 시간복잡도로 풀 수 있음.

💡 DP 를 푸는 과정

1. 테이블 정의하기
2. 점화식 찾기
3. 초기값 정하기

예시 문제 1. 1로 만들기

• 링크 : https://www.acmicpc.net/problem/1463

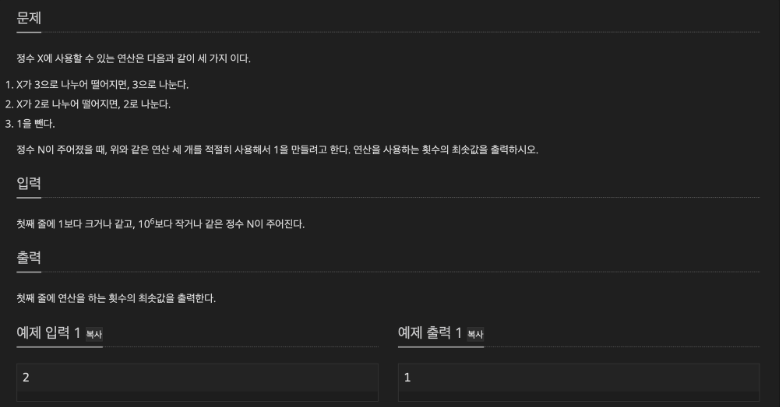
1. 테이블 정의하기

   dp[i] : i 를 1로 만들기 위한 연산 사용 횟수의 최솟값으로 잡음.

   dp[n] 이 주어졌을 때 다음 dp[n+1] 을 이전 연산 기준으로 진행할 수 있기 때문.

2. 점화식 찾기

   각 값의 놓고 생각해보기.

   dp[12] 이전의 값들을 모두 알고 있다고 생각해보자. 그렇다면 dp[12]의 이전의 연산 과정을 생각해보면

   3으로 나누거나 (dp[12] = dp[4] + 1)

   2로 나누거나 (dp[12] = dp[6] + 1)

   1을 빼거나 (dp[12] = dp[11] + 1)

   인 것을 알 수 있다. 여기서 우리는 점화식을 추론할 수 있다.

   dp[n] = min(dp[n/3] + 1, dp[n/2] + 1, dp[n-1] + 1)

3. 초기값 정하기

   해당 문제에서 초기값은 DP[1] = 0이다.

정답 코드

package 동적계획법;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

// 1463 1로 만들기
public class boj_1463 {

  public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    int n = Integer.parseInt(br.readLine());
    int[] dp = new int[n + 1];
    for (int i = 2; i < n + 1; i++) {
      dp[i] = dp[i - 1] + 1;
      if (i % 2 == 0) {
        dp[i] = Math.min(dp[i], dp[i / 2] + 1);
      }
      if (i % 3 == 0) {
        dp[i] = Math.min(dp[i], dp[i / 3] + 1);
      }
    }
//    System.out.println(dp[n]);
    Arrays.stream(dp).forEach(System.out::println);
    br.close();
  }
}

예시 문제 2. 피보나치 함수

• 링크 : https://www.acmicpc.net/problem/1003

1. 테이블 정의하기

   문제가 이해하기 힘들어 보이지만 간단하게 재귀로 피보나치 함수를 구현했을 때, 가장 마지막 재귀값인 0, 과 1이 얼마나 호출됐는지 구하는 문제이다.

   나는 dp[n] 일때 가지는 (0의 개수, 1의 개수) 를 테이블로 삼았다.

2. 점화식 찾기

   간단히 생각해보자. (0의 개수, 1의 개수) 라고 할 때,

   dp[2] = dp[1](0,1) + dp[0](1,0) → (1,1)

   dp[3] = dp[2] + dp[1] → dp[1](0,1) + dp[0](1,0) + dp1 → (1,1) + (0,1)

   dp[4] = dp[3] + dp[2] → dp[2] + dp[1] + dp[1] + dp[0] → (1,2) + (1,1)

3. 초기값 정하기

   초기값은 기존 피보나치와 같이

   dp[0] = (1,0)

   dp[1] = (0,1)

   이다.

구현 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;

// 피보나치 함수
public class boj_1003 {

  public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    int tc = Integer.parseInt(br.readLine());
    StringBuilder sb = new StringBuilder();

    List<ST> dp = new ArrayList<ST>();

    dp.add(0, new ST(1, 0));
    dp.add(1, new ST(0, 1));

    for (int i = 2; i < 41; i++) {
      dp.add(i, ST.plus(dp.get(i - 1), dp.get(i - 2)));
    }

//    dp.stream().forEach(i -> System.out.println(i.toString())); // 테스트

    for (int t = 0; t < tc; t++) {
      int n = Integer.parseInt(br.readLine());
      sb.append(dp.get(n).toString()).append('\n');
    }
    System.out.println(sb.toString());
    br.close();
  }

  public static class ST {

    int zeroCount;
    int oneCount;

    public ST(int zeroCount, int oneCount) {
      this.zeroCount = zeroCount;
      this.oneCount = oneCount;
    }

    static ST plus(ST st0, ST st1) {
      return new ST(st0.zeroCount + st1.zeroCount, st0.oneCount + st1.oneCount);
    }

    @Override
    public String toString() {
      return String.format("%d %d", this.zeroCount, this.oneCount);
    }
  }

}

결론.

DP 문제는 개인적으로 많이 풀고 외우는게 장땡이라고 생각한다.

나올 수 있는 문제가 아주 많거니와 테이블을 어떻게 세우느냐가 관건이기 때문이다.