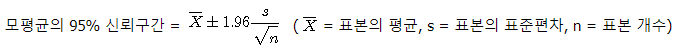모집단(Population): 알고싶은 대상의 전체 데이터
표본 (Sample): 그 대상의 일부 데이터
우리는 모집단에 대한 가설을 수립한다.
표본을 통해 가설이 맞는지 검증하는 과정이 가설검정이다.
자료의 종류에 맞게 X->Y 에 대해서 그래프(시각화)와 가설검정(수치화)을 수행하고 결과를 평가합니다.
검정통계량
- 종류: t통계량, 카이제곱 통계량, f통계량 등..
- 각각의 분포를 가진다.
- 분포를 통해 그 차이의 정도로 판단한다.
- 수치화 시켜서 나타낸 것이 pvalue
다변량 분석 정리표
X(독립변수)-->Y(종속변수)일 때 X와 Y 변수의 유형이 연속형(숫자형)인지 범주형인지에 따라 시각화 및 가설검정 수행 방법이 달라진다.
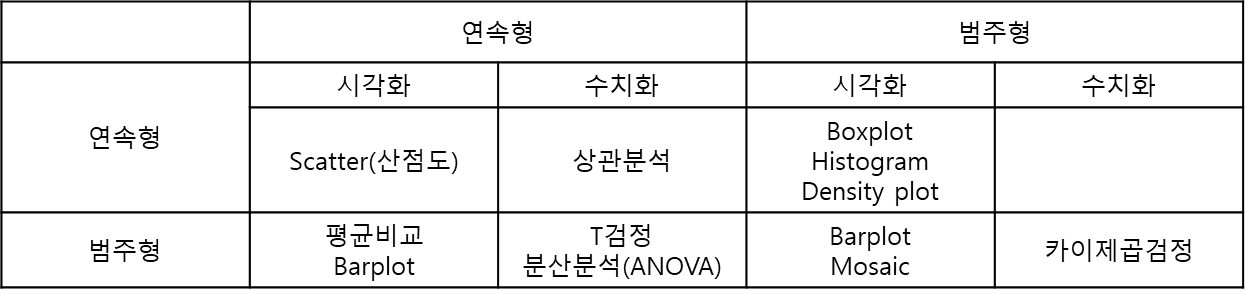
* 숫자 -> 숫자 : 상관분석
* (독립변수)범주 -> 숫자 : t검정, 분산분석(anvoa)
* 숫자 -> 범주 : 로지스틱 회귀분석 (회귀모형의 회귀계수 P.value)
* 범주 -> 범주 : 카이제곱검정다변량 분석, 연속형 -> 연속형
두 연속형 변수의 관계에서의 관점은 '직선'(Linerity)를 파악하는 것이다.
공분산(共分散, 영어: covariance)은 2개의 확률변수의 선형 관계를 나타내는 값이다. 만약 2개의 변수중 하나의 값이 상승하는 경향을 보일 때 다른 값도 상승하는 선형 상관성이 있다면 양수의 공분산을 가진다.
시각화
🔸 plt.scatter(x축값, y축값)
🔸 sns.scatterplot(x변수, y변수, data=df)
🔸 sns.regplot(x변수, y변수, data=df)
🔸 sns.jointplot(x변수, y변수, data=df)
🔸 sns.pairplot(df)
▪ plt scatter() 예시, 보스턴 집값 데이터셋
seaborn.scatterplot — seaborn 0.12.2 documentation
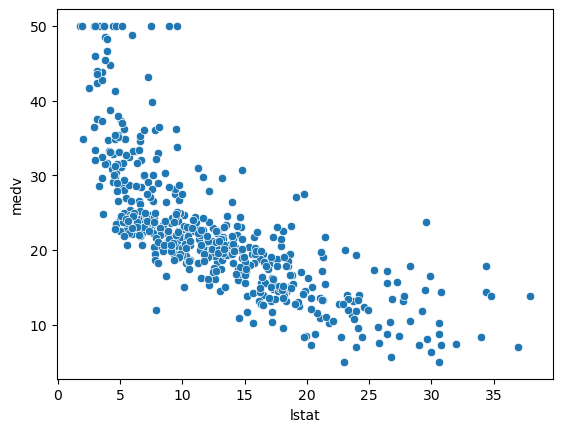
음수의 공분산을 갖고있는 강한 상관관계를 보여준다.
# lstat(하위계층비율) -> mdev(집값)
plt.scatter(boston['lstat'], boston['medv'])
plt.show()
# plt.scatter('lstat', 'medv', data = boston)
sns.scatterplot(x='lstat', y='medv', data=boston)
plt.show()▪ regplot() 예시
seaborn.regplot — seaborn 0.12.2 documentation
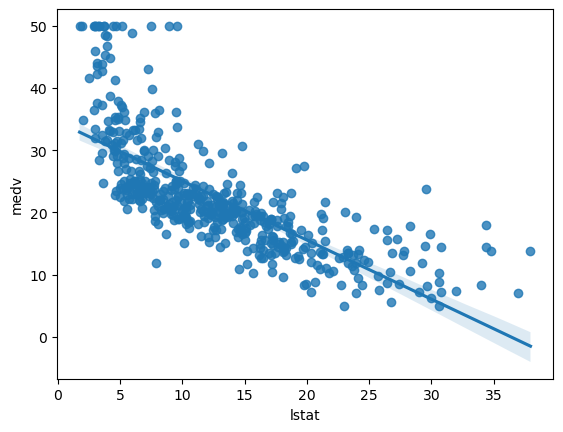
sns.regplot(x='lstat', y='medv', data=boston)
plt.show()▪ jointplot() 예시
seaborn.jointplot — seaborn 0.12.2 documentation
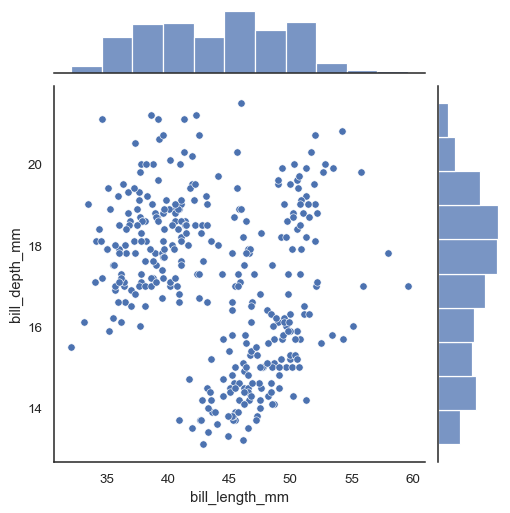
▪ pairplot() 예시
seaborn.pairplot — seaborn 0.12.2 documentation
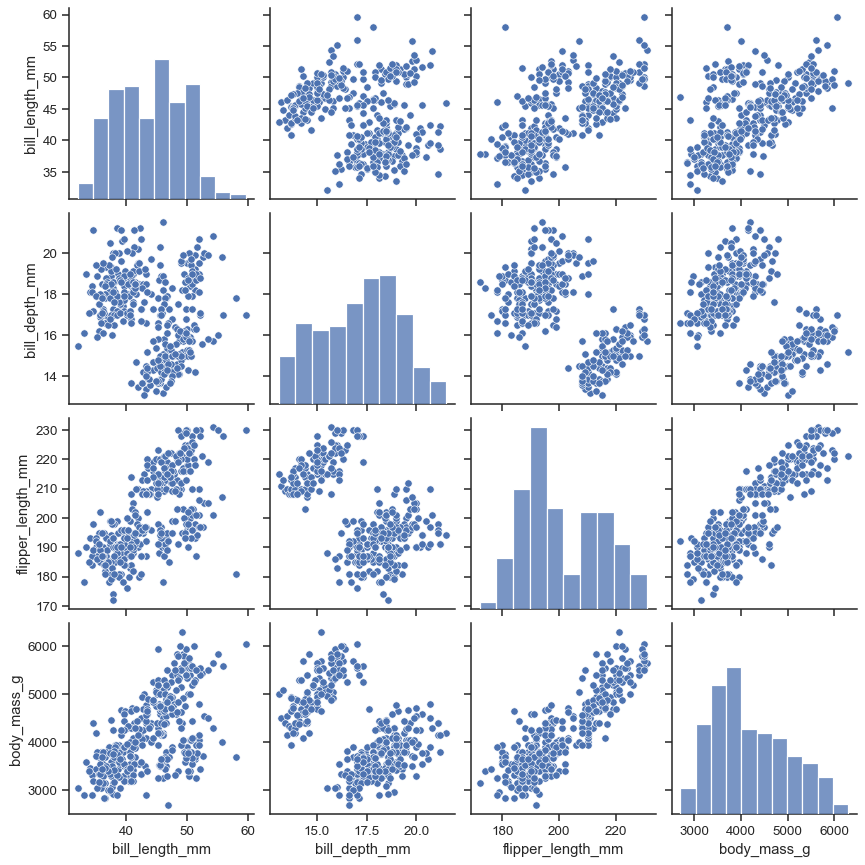
수치화
시각화를 통해서 눈으로 확인했다면 다음은 관계를 수치화하는데 사용하는 것이 상관계수다.
상관계수 검정을 상관분석이라고 한다.
상관계수 (correlation) : r 로 표현
- -1 ~ 1사이의 값
- -1, 1에 가까울수록 상관관계가 높다.
피어슨 상관분석 scipy.stats모듈
- 주의: 데이터에 NaN이 있으면 계산 불가
import scipy.stats as spst
# lstat(하위계층비율) -> mdev(집값)
spst.pearsonr(boston['lstat'], boston['medv'])- 결과: 튜플형태 (상관계수, p-value)
PearsonRResult(statistic=-0.7376627261740148, pvalue=5.081103394387554e-88)
p-value(유의확률)
- 귀무가설이 옳다고 가정했을 때, 통계치가 관측될 확률
- p-value < 0.05, 즉 확률이 5% 미만인 경우 신뢰구간 95%에 포함되지 않음으로 귀무가설을 기각하고 대립가설이 맞다고 판단
df.corr()
데이터 타입이 수치형(int, float)인 경우 변수간의 상관계수 값이 나타난다.
타이타닉 데이터 예시
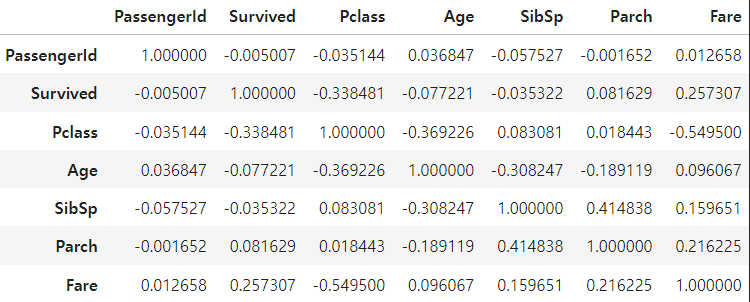
상관계수의 한계
직선의 기울기, 비선형 관계는 전혀 고려되지 않는다.
다변량 분석, 연속형 -> 범주형
시각화
95% 신뢰구간(Confidence Interval)
표본이 100개를 샘플링하여 각각의 신뢰구간을 구했을때 95번은 모집단의 평균을 포함한다.
데이터가 많을수록, 편차가 적을수록 신뢰구간은 좁아진다.(편차가 적을 수록 값이 밀집) 신뢰구간은 좁을 수록 믿을만하다. 즉 오차범위가 적을수록 좋다.
🔸 sns.barplot(x변수, y변수, data=df)
sns.barplot(x="Survived", y="Age", data=titanic)
plt.grid()
plt.show()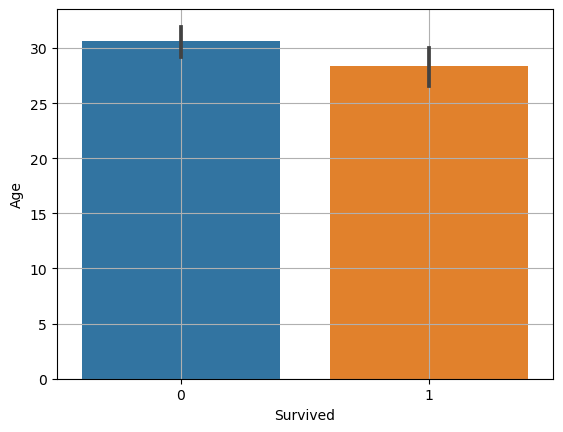
해석: 신뢰구간이 겹침으로 성별에 따른 생존여부는 관계가 크지 않다.
수치화
NaN의 값을 제거하고 수행한다.
t-test: 독립변수 범주가 2개
두 그룹간의 평균차이를 표준오차로 나눈 값
t 통계량: -2보다 작거나 2보다 크면 차이가 있다.
<예제>
귀무가설: 타이타닉 탑승객 생존 여부별 나이의 차이가 없다.
대립가설: 타이타닉 탑승객 생존 여부별 나이의 차이가 있다.
반드시 범주별 데이터를 나누고 ttest_ind()사용
# 타이타닉 t-test검정
temp = titanic.loc(titanic['Age'].notnull()]
# 범주화 데이터 저장
die = temp.loc[temp['Survived']==0, 'Age']
survive = temp.loc[temp['Survived']==1,'Age']
#t-ttest
spst.ttest_ind(die, survive) # (t통계량 , p-value)
spst.ttest_ind(survive,die) # survive의 부호만 반대 위에와 값은 동일
# 결과 #
Ttest_indResult(statistic=-2.06668694625381, pvalue=0.03912465401348249)
# 해석 #
-2.06 : 2보다 작음으로 차이가 조금 있다.
0.039 : 0.05보다 작음으로 차이가 조금 있다.
t-test가 음수인 이유는 두 평균의 차이 임으로 die, survive의 작성 순서에 따라서 달라진다.
ANOVA((ANalysis Of VAriance): 독립변수 범주가 2개 이상
여러 집단간의 차이 비교
f통계량 = 집단 간 분산 / 집단 내 분산
= 전체평균 - 각 집단 평균 / 각 집단의 평균 - 개별 값
값이 2~3 이상이면 차이가 있다고 판단
<예제>
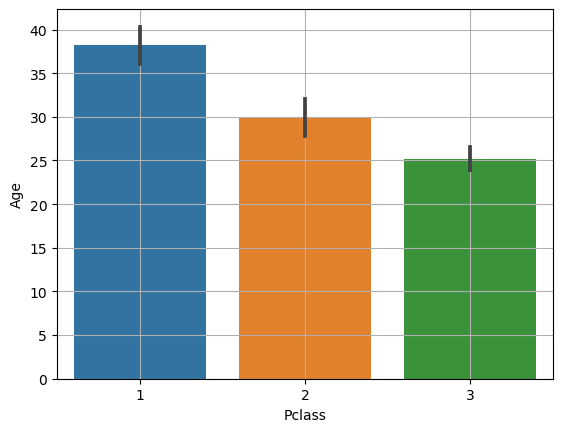
해석: Pclass 마다 차이가 큰 것으로 보인다.
# 분산 분석을 위한 데이터 만들기
# NaN 행 제외 (그룹별 저장을 할 때 nan이 자동으로 빠짐)
temp = titanic.loc[titanic['Age'].notnull()]
# 그룹별 저장
P_1 = temp.loc[temp.Pclass == 1, 'Age']
P_2 = temp.loc[temp.Pclass == 2, 'Age']
P_3 = temp.loc[temp.Pclass == 3, 'Age']
spst.f_oneway(P_1, P_2, P_3)
F_onewayResult(statistic=57.443484340676214, pvalue=7.487984171959904e-24) #(f통계량, pvalue)
# 해석 #
f통계량은 집단 간의 분산이 집단 내의 분산보다 57.443배 더 크다는 의미
다변량 분석, 범주형 -> 범주형
교차표 (crosstab)
https://pandas.pydata.org/docs/reference
/api/pandas.crosstab.html
범주형 변수와 범주형 변수끼리는 교차표로 집계하여 시각화, 수치화에 모두 사용된다.
pd.crosstab(행, 열, normalize= )
- normalize 옵션: 비율로 반환 / value_counts(normalize=True)에서도 사용
- columns : 열 기준
- index : 행 기준
- all : 전체 기준
pd.crosstab(titanic['Survived'], titanic['Sex'])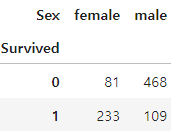
pd.crosstab(titanic['Survived'], titanic['Sex'], normalize = 'columns')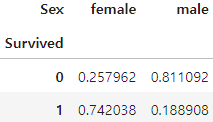
pd.crosstab(titanic['Survived'], titanic['Sex'], normalize = 'index')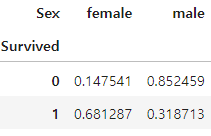
pd.crosstab(titanic['Survived'], titanic['Embarked'], normalize = 'all')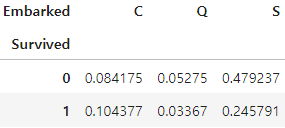
시각화
🔸 mosaic(dataframe, [feature, target])
mosaic(titanic, [ 'Pclass','Survived']) 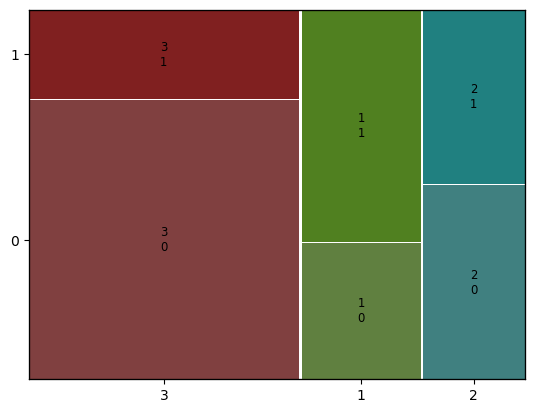
해석: x축은 Pclass의 승객 비율을 나타내고 y축은 각 등급별 생존자와 사망 비율을 나타낸다. (1:생존)
수치화
카이제곱 검정 (chi-squared test)
: 기대빈도와 실제 데이터의 차이
: 두 범주형 변수가 서로 상관이 있는지 독립인지를 판단

- 결과값이 클수록 기대값과 실제값 간의 차이가 크다
- 집단간의 수가 많을 수록 값은 커진다.
- 자유도의 2배보다 크면 차이가 있다고 본다.
자유도란 : 범주의 수 - 1
즉, 범주형 변수 값의 유형 갯수 - 1
<예시>
타이타닉 Pclass -> Survived
자유도 계산
(3-1) * (2-1) = 2 (자유도는 2)
따라서 2의 2배인 4 이상이면 차이가 있다고 볼 수 있다.
# 1) 교차표 집계 , normalize 설정 안해야한다! 앞뒤 행, 열 순서는 카이제곱 통계량 수치와는 상관 없다.
table = pd.crosstab(titanic['Survived'], titanic['Pclass'])
# 2) 카이제곱검정
spst.chi2_contingency(table)
# 결과 #
Chi2ContingencyResult(statistic=102.88898875696056, pvalue=4.549251711298793e-23, dof=2, expected_freq=array([[133.09090909, 113.37373737, 302.53535354],
[ 82.90909091, 70.62626263, 188.46464646]]))
# 해석 #
카이제곱 통계량, p-value, dof(자유도), expected_freq(기대빈도)