[머신러닝] 모델 평가하기

syEON·2023년 8월 29일
머신러닝
1
post-thumbnail

분류 문제 (Classification) : 범주형 변수 데이터를 적절히 분류하는 것 / 지도학습
회귀 문제(Rregression): 수치형 변수의 값을 예측 하는 것 / 지도학습

분류, 회귀 문제에 따라 각각 다른 알고리즘 모델링과 성능 평가 모델을 사용해야 함으로 잘 숙지해야한다.

분류회귀
알고리즘 모델링DecisionTree
KNeighborsClassifier
LogisticRegression
RandomForesetClassifier
XGBClassifier		LinearRegression
KNeighborsRegressor
DecisionTreeRegressor
RandomForestRegressor
XGBRegressor
성능 측정, 평가accuracy_socre
recall_score
preicsion_score
classification_report
confusion_matrix
f1-score		mean_absolute_error
mean_squared_error
root_mean_squared_error
mean_absolute_percentage_error
r2_score

모델 성능평가에 들어가기 앞서 데이터 분리 코드를 간단하게 정리하였다.

데이터 분리

# 모듈 불러오기
from sklearn.model_selection import train_test_split

# 7:3으로 분리
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=1, shuffle = True, stratify = y)  
# shuffle은 default가 True라서 명시하지 않아도 된다.
# stratify는 target 변수로 지정. 의미: label데이터 값의 비율(갯수)을 동일하게 나눈다.

모델 평가

  • 분류 모델 평가: 실제값과 예측값이 많이 맞을수록 우수, 정확도를 높이자!
  • 회귀 모델 평가: 실제값과 예측값 차이(=오차) 가 작을 수록 우수, 오차를 줄이자!

[기호 정리]

yy : 실제값, 우리가 예측하고 싶은 Target의 값

y^\hat{y} : 예측값, 우리가 모델로 예측한 Target의 값

yˉ\bar{y} : 평균값, 예측값이 평균값보다 오차를 얼마나 더 줄였는지 중요

모델 평가하기 공통 코드
함수(실제값, 예측값) #실제값, 예측값 변수의 순서가 변경되어도 상관없는 함수들이 있지만 아닌경우도 있음으로 유의한다!!

회귀 모델 평가

SSE, MSE, RMSE, MAE, MAPE 모두 오류이므로 작을 수록 좋다.

특징
MSE는 제곱한 형태로 오차값이 이차원 그래프 형식으로 그려진다.
어떤 값이든 미분이 가능하다.
그러나 오차를 제곱한 형태임으로 이상치에 대한 영향을 많이 받는다.
상대적으로 MSE> RMSE > MAE 가 이상치에는 덜 민감하지만 미분이 안되는 구간도 있다.

  • SSE (Sum Squared Error) : 오차 제곱의 합
    오차: 실제값과 예측값에 대한 차이, 아직 해결하지 못한 값)

     SSE=∑i=1n(y^i−yi)2\ SSE=\sum_{i=1}^{n}(\hat{y}_{i}-{y}_{i})^2

  • MSE (Mean Squared Error) : SSE의 평균
    라이브러리: from sklearn.metrics import mean_squared_error

     MSE=1n∑i=1n(yi−y^i)2\ MSE=\frac{1}{n}\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^2

  • RMSE (Root Mean Squared Error) : MSE의 루트 값

     RMSE=1n∑i=1n(yi−y^i)2\ RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^2}

    라이브러리는 따로 없고 MSE 라이브러리를 사용하여 변경한다. 

    mean_squared_error(y_test, y_pred)**(1/2)   #방법1
mean_squared_error(y_test, y_pred, squared=False)   #방법2

  • MAE (Mean Absolute Error): 오차 절대값 합의 평균
    라이브러리: from sklearn.metrics import mean_absolute_error

     MAE=1n∑i=1n∣yi−y^i∣\ MAE=\frac{1}{n}\sum_{i=1}^{n}|y_{i}-\hat{y}_{i}|

  • MAPE (Mean Absolute Percentage Error) : MAE를 비율화
    라이브러리 : from sklearn.metrics import mean_absolute_percentage_error

     MAPE=1n∑i=1n∣yi−y^iyi∣\ MAPE=\frac{1}{n}\sum_{i=1}^{n}\left |\frac{y_{i}-\hat{y}_{i}}{y_{i}}\right |




오차에 대한 여러 시각

  • SSE (Sum Squared Error): 실제값 - 예측값 , 아직 해결하지 못한 값

     SSE=∑i=1n(y^i−yi)2\ SSE=\sum_{i=1}^{n}(\hat{y}_{i}-{y}_{i})^2

  • SSR (Sum Squared Regression): 예측값 - 평균값, 클수록 좋은 성과

     SSR=∑i=1n(y^−yˉ)2\ SSR=\sum_{i=1}^{n}(\hat{y}-\bar{y})^2

  • SST (Sum Squared Total): 실제값 - 평균값, 우리에게 주어진 최대 오차 범위

     SST=∑i=1n(yi−yˉ)2\ SST=\sum_{i=1}^{n}(y_{i}-\bar{y})^2

  • SST = SSR + SSE
  •  R2\ R^2 (R-Squared) : 결정계수
    라이브러리 : from sklearn.metrics import r2_score
    전체 오차 중에서 회귀식이 잡아낸 오차 비율 (일반적으로 0~1 사이)
    클수록 오차가 적은 것

     R2=SSRSST=1−SSESST=1−∑i=1n(yi−y^i)2∑i=1n(yi−yˉi)2\ R^2= \frac{SSR}{SST} = 1-\frac{SSE}{SST}=1-\frac{\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^2}{\sum_{i=1}^{n}(y_{i}-\bar{y}_{i})^2}
    SST(전체 오차)에서 SSR(회귀식을 통해 잡아낸 오차)의 비율, 즉 얼마나 오차를 잡아냈나!
    => 값이 클수록 성공!!


실습

mean_absolute_error(y_test, y_pred)
mean_squared_error(y_test, y_pred)
#RMSE 구하는 방법
mean_squared_error(y_test, y_pred)**(1/2)   #방법1
mean_squared_error(y_test, y_pred, squared=False)   #방법2
mean_absolute_percentage_error(y_test, y_pred)
r2_score(y_test, y_pred)

공통 모델 평가

score()를 하면 r2_score()와 동일한 결과가 나오는 것으로 보아 회귀 모델의 score는 r2_score()를 사용하고 있다.
테스트데이터 셋을 인자로 작성해야 함을 주의한다!!

model.score(x_test, y_test)

분류 모델 평가

혼동행렬 분석

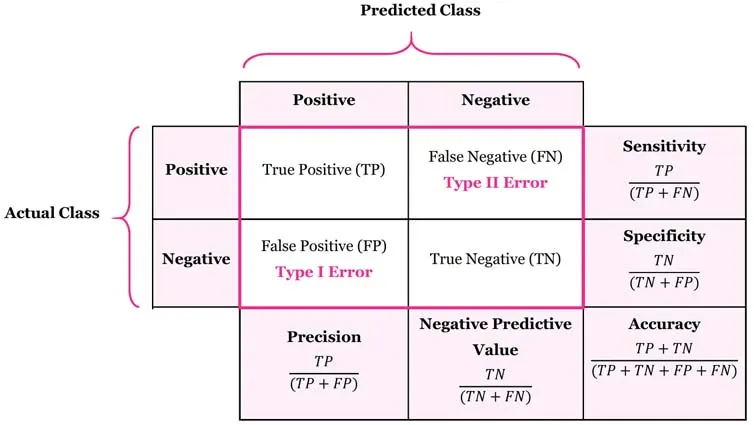
뒷 글자가 Predict, 앞 글자가 Actual 실제값이다.
정밀도와 재현율은 기본적으로 Positive에 대해 값이다. 평가함수 파라미터에 average=None을 적으면 Negative에 대한 값도 같이 볼수 있다.



  • Confusion Matrix : 혼동행렬의 갯수
    라이브러리: from sklearn.metrics import confusion_matrix
    코드: confusion_matrix(y_test, y_pred)
    결과 예시 heatmap으로 변경 코드 
 sns.heatmap(confusion_matrix(y_test, y_pred),
           annot=True,
           cmap='Blues',
           cbar=False,
           annot_kws={'size':12})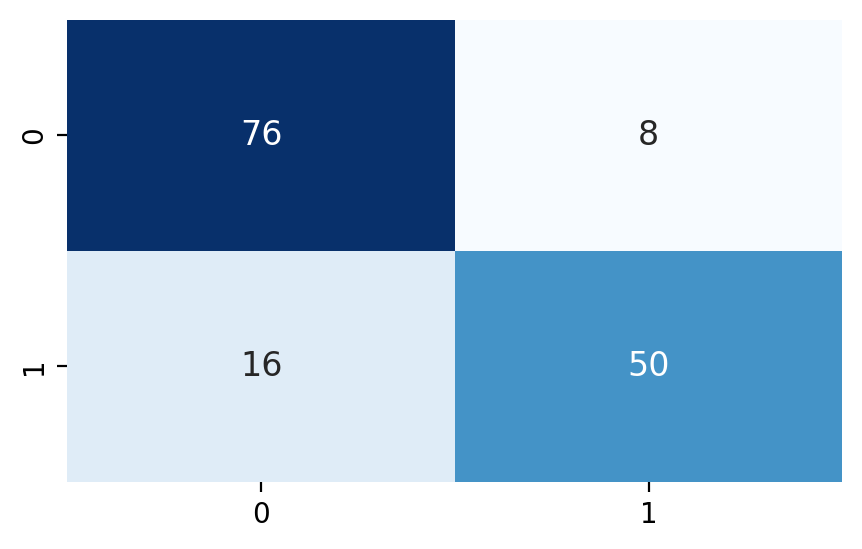

  • Accuracy: 정확도 (TN + TP)
    라이브러리: from sklearn.metrics import accuracy_score

     Accuracy=TP+TNTP+TN+FP+FN\ Accuracy = \frac{TP+TN}{TP+TN+FP+FN}

  • Precision: 정밀도 (FP + TP) , 예측값 기준

     Precision=TPTP+FP\ Precision = \frac{TP}{TP+FP}
    label의 데이터가 이중분류, 삼중분류에 따라 파라미터를 유의해야한다.

print(sklearn.metrics.precision_score(y_test, y_pred))   # 결과: default는 정밀도 1 (posivie기준 값)
print(sklearn.metrics.precision_score(y_test, y_pred, average=None)) #정밀도 0, 정밀도 1  #다중분류일 때 이렇게 사용해야 에러 없다!
print(sklearn.metrics.precision_score(y_test, y_pred, average='binary')) #첫번째 default의 averge값이 binary

print(sklearn.metrics.precision_score(y_test, y_pred, average='macro')) #평균 
print(sklearn.metrics.precision_score(y_test, y_pred, average='weighted')) #가중치 평균
  • Recall: 재현율 (FN+ TP), 실제값 기준
    라이브러리: from sklearn.metrics import recall_score

     Recall=TPTP+FN\ Recall = \frac{TP}{TP+FN}

sklearn.metrics.recall_score(y_test, y_pred, average=None)
  • f1-score: 정밀도 + 재현율 조화 평균
    라이브러리: from sklearn.metrics import f1_score

     F1=2×Precision×RecallPrecision+Recall\ F1 = \frac{2\times Precision\times Recall}{Precision+Recall}

sklearn.metrics.f1_score(y_test, y_pred, average=None)
  • classification_report
    라이브러리: from sklearn.metrics import classification_report
    결과 예시

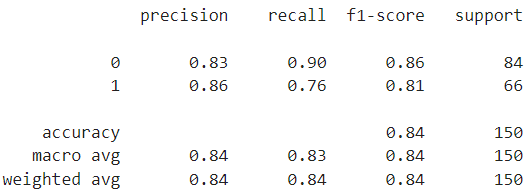
macro avg: 위의 각 분류마다의 평균 값 ex 0.83과 0.86의 평균 0.84
weighted avg: 가중치 평균으로 0, 1의 데이터 갯수에 따른 가중치를 두어 계산
support: 분류별 평가 데이터의 갯수 및 총합 (분류별 데이터의 갯수가 같기 위해서는 데이터셋을 나눌때 stratify = y 파라미터를 지정한다!)


Specificity
특이도, Negative중에서 Negative로 예측한 비율 (TN + FP)
코로나의 음성확인자를 판별하는 과정에서 Specificity가 중요해졌다.

공통 모델 평가
score()를 하면 accuracy()와 동일한 결과가 나오는 것으로 보아 분류 모델의 score는 accuracy()를 사용하고 있다.
테스트데이터 셋을 인자로 작성해야 함을 주의한다!!

model.score(x_test, y_test)  #accuracy
profile
syEON
:)
이전 포스트

Data Understanding: EDA, CDA(2)

다음 포스트

[머신러닝] 기본 알고리즘 LinearRegression, KNN, DecisionTree, LogisticRegression

0개의 댓글