1446 : 지름길

김준태·2023년 10월 26일

DP 백준

코딩테스트

목록 보기

11/13

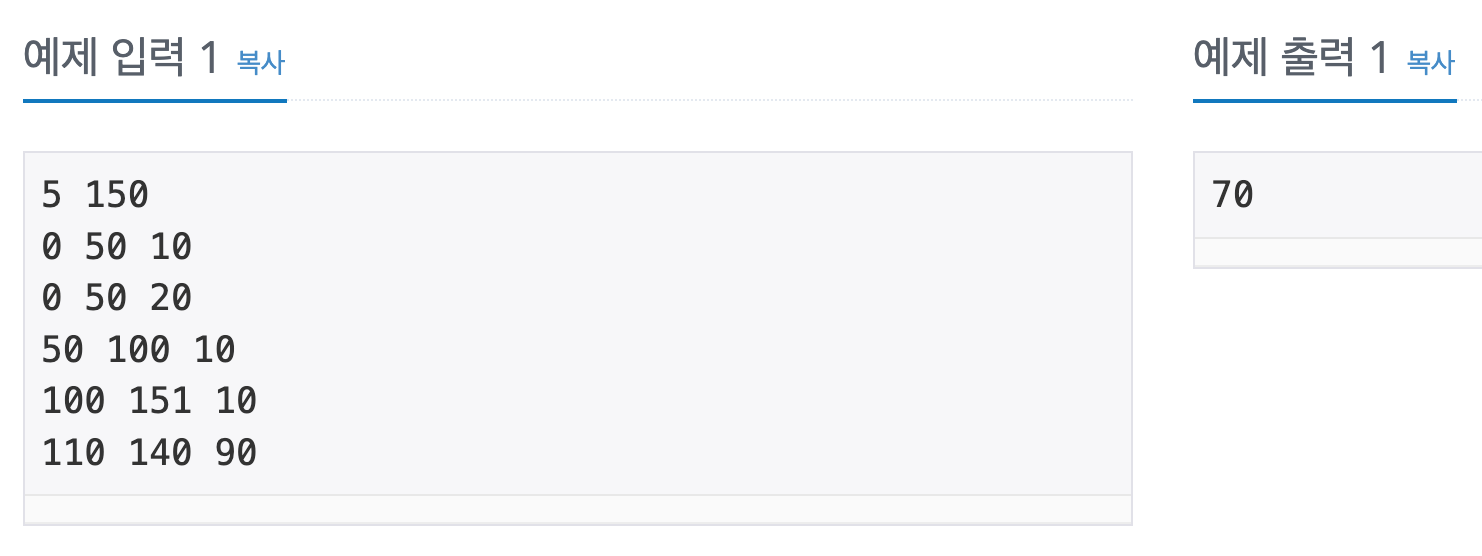
☀️ 문제 링크

https://www.acmicpc.net/problem/1446

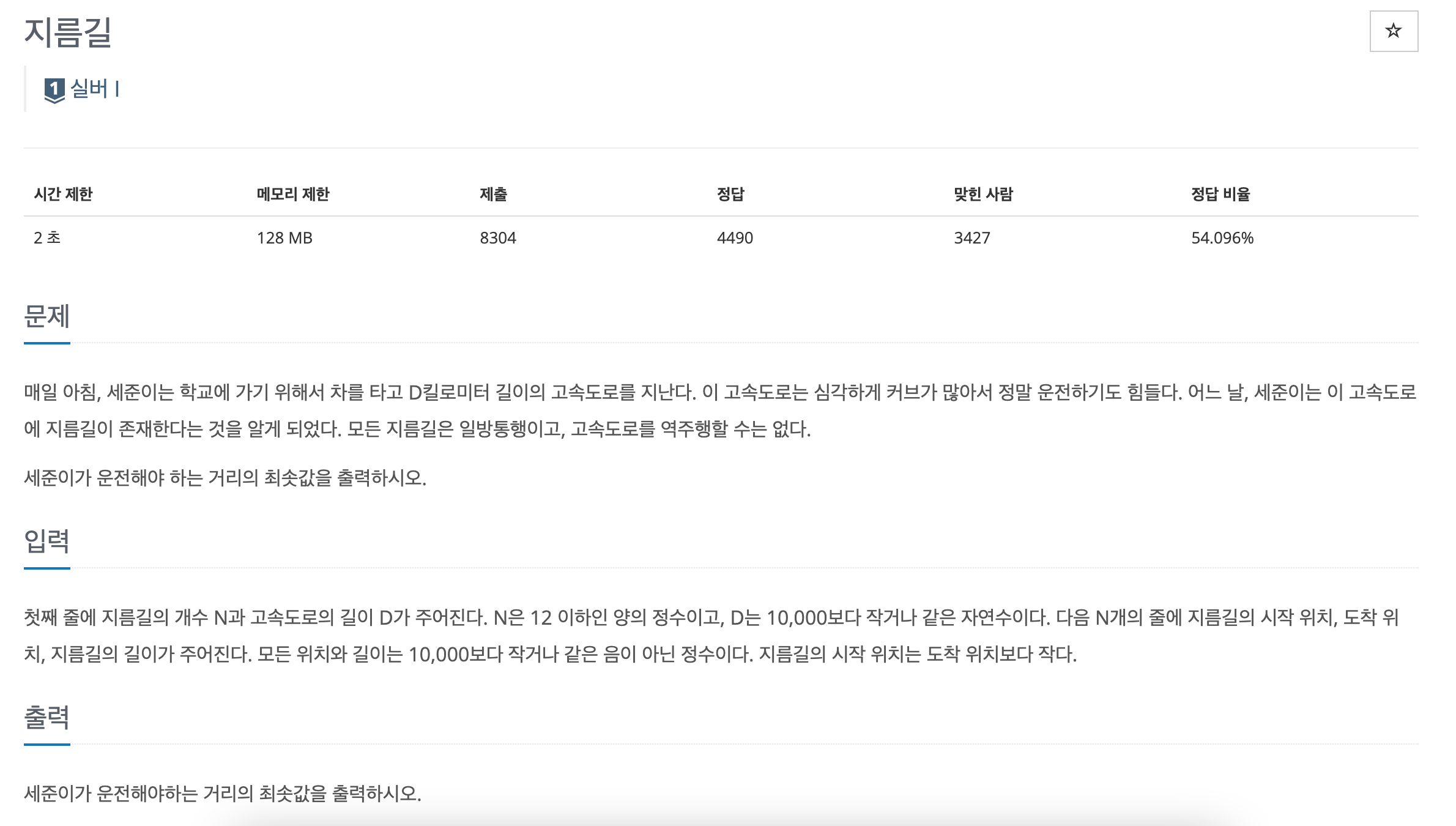
🌻 문제 간단한 설명

DP를 활용해서 최소 이동거리를 구하는 문제이다.

if(지름길이 있고 && 그냥 이동하는 거리 < 지름길을 이용하는 거리) 일경우 지름길을 선택한다.

예) 0 -> 50 (그냥 이동거리 50)

지름길 (0 50 10) 이용시 이동거리 10

50 < 10 이므로 dp[50] 의 값은 10 이다.

⚡️ 풀이

🌝 전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int[] dp = new int[M + 1];
        int[][] shortcuts = new int[N][3];

        for (int i = 0; i < N; i++) {
            shortcuts[i] = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
        }

        Arrays.sort(shortcuts, (o1, o2) -> o1[0] - o2[0]);

        for (int i = 1; i <= M; i++) {
            dp[i] = dp[i - 1] + 1;
            for (int[] shortcut : shortcuts) {
                if (i == shortcut[1]) {
                    dp[i] = Math.min(dp[i], dp[shortcut[0]] + shortcut[2]);
                }
            }
        }

        System.out.println(dp[M]);
    }
}

🌛 코드별 설명

입력받고 배열 생성하는 부분은 생략한다.

정렬

지름길의 시작지점을 기준으로 정렬해준다.

정렬에는 다양한 방법이 있다.

// 참고로 이건 오름차순
Arrays.sort(shortcuts, (o1, o2) -> o1[0] - o2[0]);

or

Arrays.sort(shortcuts, Comparator.comparingInt(o -> o[0]));

// 이건 내림차순
Arrays.sort(shortcuts, (o1, o2) -> o2[0] - o1[0]);

DP 값 입력 & 정답 출력

for (int i = 1; i <= M; i++) {
	// dp[1] = 1 거리 기본값 저장
    dp[i] = dp[i - 1] + 1;
    // 지름길 하나씩 순회하면서 탐색 (최대길이 12)
    for (int[] shortcut : shortcuts) {
    	// i = 현재거리 / shortcut[1] = 지름길 도착위치
        if (i == shortcut[1]) {
        	// Math.min의 비교값 설명
        	// dp[i] -> 지름길을 타지 않았을 경우의 거리
            // dp[shortcut[0](지름길 시작지점)] -> 지름길 시작지점의 최소이동거리
            // shrtcut[2] -> 지름길을 이동했을 경우 소요 이동거리
            dp[i] = Math.min(dp[i], dp[shortcut[0]] + shortcut[2]);
        }
    }
}

System.out.println(dp[M]);