OS - 2.6 (MV) (6) Multi-Level Page Tables

  현재 Paging에 관해 열심히 공부하고 있다. 잠시 멈추고, 우리가 이 개념을 공부하는 근본적인 이유를 복기해보자. Process Loading이다. 우리는 지금 Process의 Loading 방법에 대해 논하고 있다.

  Loading 시, 연속적인 할당은 External Fragmentation이 높아 폐기한다고 했다. 그래서 Page 단위로 잘라서 Load하는 Paging이 도입된 거였다. 비연속적인 할당을 도모한 것이다. 물론, 이로 인해 Internal Fragmentation이 조금 올라가지만, 그래도 이정도는 괜찮은 것이다.

~> 그런데, 여기서 새로운 문제가 발생한 것이다. 비연속적으로 할당하다 보니, 어떤 Page가 어디에 있는지를 알아야 했다. 그래서 Page Table이 도입된 것이다.

~> 허나, Page Table은 그 자체가 너무 크다. 모든 Process에게 하나씩 있어야 함을 고려하면 더더욱 그 크기는 부담스럽다.
~~> 그래서, Main Memory에 Page Table을 두기로 결정한 것이다.

~> 하지만, 이에 따라 Double Memory Access 문제가 떠올랐고, 여기서 바로 직전 포스팅에서 배운 TLB 개념이 등장한 것이다. MMU HW 안에 TLB라는 Cache를 두어 조금 더 빠른 메모리 접근을 도모한다.

그런데 이때, Page Table은 어디있는가. TLB를 쓰든 안쓰든 여전히 Main Memory에 존재한다.

그리고, VAS의 일부 공간은 사용하지 않는대도 불구하고 Page Table에 맵핑된다.

뭔가, Page Table 그 자체의 크기를 줄일 방법이 있지 않을까?

Some Problems

Size of Page Table

• 각 Process에 대해 Page Table이 존재한다.

  • 32-Bit Machine일 경우, Address는 32Bits로 표현된다.

    • 즉, 2^32 = 4GB의 Virtual Address Space를 가진다.

  • Page 크기가 4KB라 할 경우, Offset이 4K = 2^12, 즉, 12Bits로 표현되는 것이고, 그말은 즉, Page의 개수는 2^20 = M개임을 의미한다.

    • 만약, Page Table의 Entry가 4Bytes이면, 이는 각 Process마다 4MB의 Page Table이 있어야 한다는 것이다. ★★★
      • Process가 많아지면 이는 너무나 큰 공간 부담이다.
        • 나아가, 이러한 Page Table은 연속적인 메모리 공간이라 다른 문제도 야기한다. ★

Page Tables are too huge. They consume too much memory.

만약, Offset의 Bits를 좀 더 늘리면 어떨까? 즉, Page 크기를 좀 더 키우고, Page 개수를 조금 줄이면 Page Table 자체를 위한 공간은 줄어들지 않을까?

• 일리 있는 말이다.

  • 위 32-Bit Machine 예시에서 Offset을 위한 Bit 개수를 14로 늘려보자.
    • Page Size는 16KB, Page 개수는 2^18개로 줄었다.
      • PTE가 4Bytes이면 Page Table의 크기는 2^20 x 4B = 1MB가 될 것이다.

• Page Table의 크기가 꽤나 줄었다. 허나, 이것이 반드시 좋은 것일까?

  • Big Page를 통해 Page Table 크기 자체는 줄었지만, 반대로 Big Page로 인한 Internal Fragmentation이 극심해진다. 불필요하게 Page가 커져, 내부에 남는 공간이 많아지는 것이다. ★★★

Unused Space

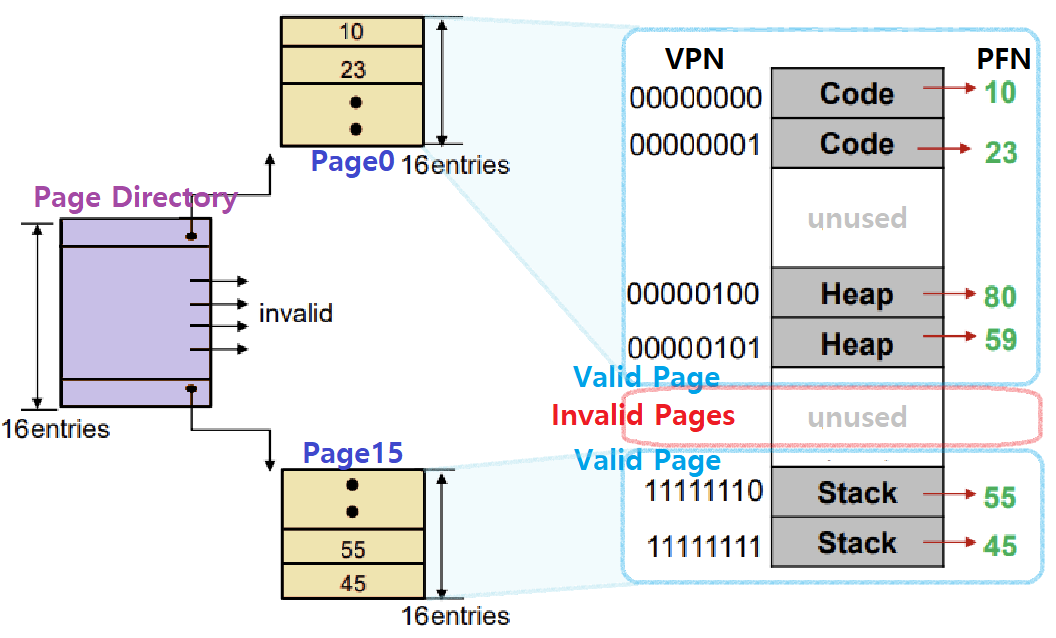
  한편, Page Table의 대부분은 Unused, 즉, Invalid Entries로 유지된다는 문제도 있다. 예를 들어, 14-Bit로 Logical Address를 표현하고, Page 크기가 1KB인 System이 있다고 하자. 당연, 10Bits는 Offset, 4Bits는 VPN으로 쓰일 것이다.

  Page Table Entry의 개수는 16개가 될터인데, PTE 사이즈 하나가 4Bytes라 하면, 총 64B가 Page Table을 위해 필요할 것이다. 아래와 같이 말이다.

• Page Table의 16개의 Entry 중 4개의 Entry만 사용되고 있는 Process이다. 나머지 12개의 Entry는 Unused로, 12/16 = 3/4 = 75%가 낭비되고 있는 것이다.
  • 이러한 작은 예시 System에서도 이정도인데, 만일 32-Bit Computer이면, 대다수의 Light한 Process에 대해선 수 많은 메모리 공간이 Page Table을 위해서 낭비될 것이다. 매 Process마다 Page Table 공간의 75%씩 낭비한다는 것이다. 기존의 Paging대로라면!

Thus, we need to 'really' unuse that unused entries!!!

~> 우리는 이제 이러한 Paging Issue에 대한 몇 가지 Solution 기법들을 알아볼 것이다. 아래를 보자.

Hybrid Approach

Paging with Segmentation

  앞에서 배웠던 Segmentation의 논리를 입히는 것이다.

Hybrid Approach : Paging & Segments

Page Table for each Segment ★★★

Process의 VAS를 Segment로 나누고, 각 Segment에 대해서 Page Table을 둔다. ★

• Segment Table을 둔다. ★★★

  • 그 Segment Table에는 각 Segment의 Page Table에 대한 BASE, BOUNDS Registers를 둔다.

• 각 Segment의 Physical Address에 대한 Page Table의 Physical Address가 시작하는 위치를 BASE Register에 담아둔다. ★

  • 그리고 해당 Page Table들의 Size(End)를 명시하는 BOUND Register를 둔다. ★

  아래와 같이 각 Process에 대해 3개의 Page Table을 운용하는 방식이 가능하다.

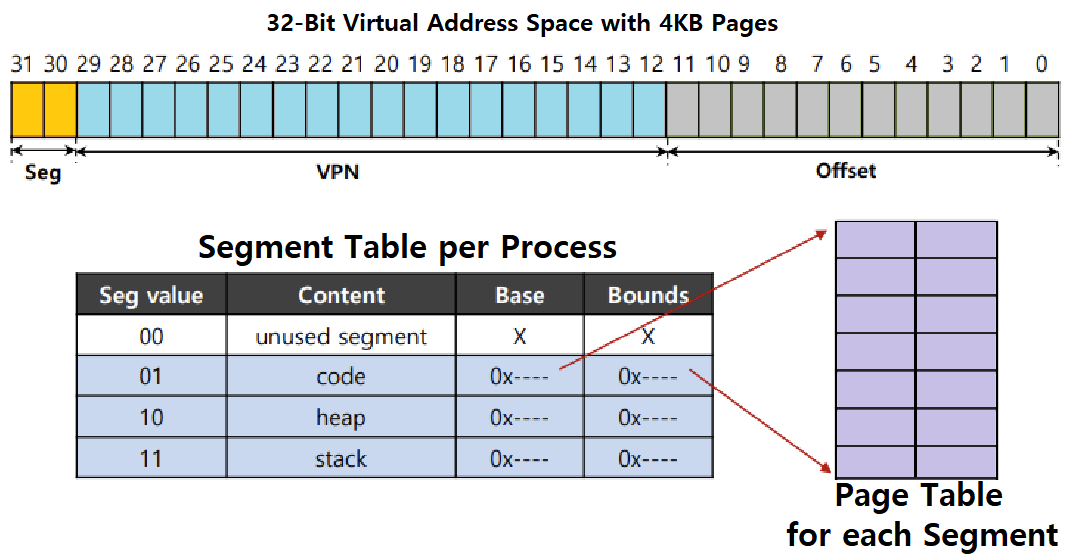
• Segment를 총 3개를 두었기 때문에 Segment Table Index를 위한 Bits를 2개 마련해두었음에 주목하자. (Logical Address Format의 변형) ★★★

  • 이로 인해 Page의 개수가 당연히 조금 줄어들 것이다. ★
  • 대신, Page Table의 Size도 줄어들 것이다. ★★★

• 각 Segment에 대해, BOUNDS 값을 줄임으로써 Page Table의 Size를 필요한만큼으로 줄일 수 있을 것이다. ★

  • Memory Waste를 줄일 수 있다. ★

SegIndex = (vaddr & SEG_MASK) >> SN_SHIFT;
VPN = (VirtualAddress & VPN_MASK) >> VPN_SHIFT;
AddressOfPTE = Base[SegIndex] + (VPN * sizeof(PTE));
/* ... */

~> 이러한 동작 방식을 지닐 것!

허나, 이러한 Hybrid Approach를 통한 Paging Problem 해결 시도는 여전히 문제가 있다.

Code, Stack Segment의 낭비는 줄일 수 있지만, Heap Segment의 낭비는 막을 수 없다. 특히 Sparsely-used Heap의 경우 이러한 단점이 두드러질 것이다. 많이 쓰지는 않지만 쓰긴 하므로 할당은 해야하고, 하지만 할당하면 공간이 많이 낭비되고,,, 그런 문제! ★★

"조금 더 획기적인 방법이 필요하다... 조금만 바꾸면 될 거 같은데..."

Multi-Level Page Tables

Page Directory

  그래서 등장한 Approach가 바로 'Multi-Level Page Table' 개념이다.

"Page Table에 대해서도 Paging을 하자!"

• Linear한 Page Table을 마치 Tree 자료구조처럼 취급하는 것이다.
  • Page Table을 Page-Size의 특정 Unit(Page)으로 쪼갠다. ★★
  • 특정 Page의 PTE들이 모두 Invalid이면, 그 Page는 애초에 할당하지 말자. ★★
    • Invalid한 Entry로 채워진 Page Table 부분(Page Size)에 대해선 아예 할당하지 말자는 것이다.
  • 특정 Page가 Valid인지 알아내기 위해, Page Directory라는 새로운 자료구조를 도입하자. ★★
    • Page Table에 대한 Page들마다 하나씩 Entry가 존재한다. (Page Directory)
      • 이러한 Entry를 PDE(Page Directory Entry)라 부르자.
        • "PDE : Valid Bit + PFN" ★★★

즉, Page Table이 Main Memory에 올라가 있고, 그것을 여러 Page로 쪼갠 후, 그 Page들을 포인팅하는 Page Directory가 따로 또 존재하는 것!

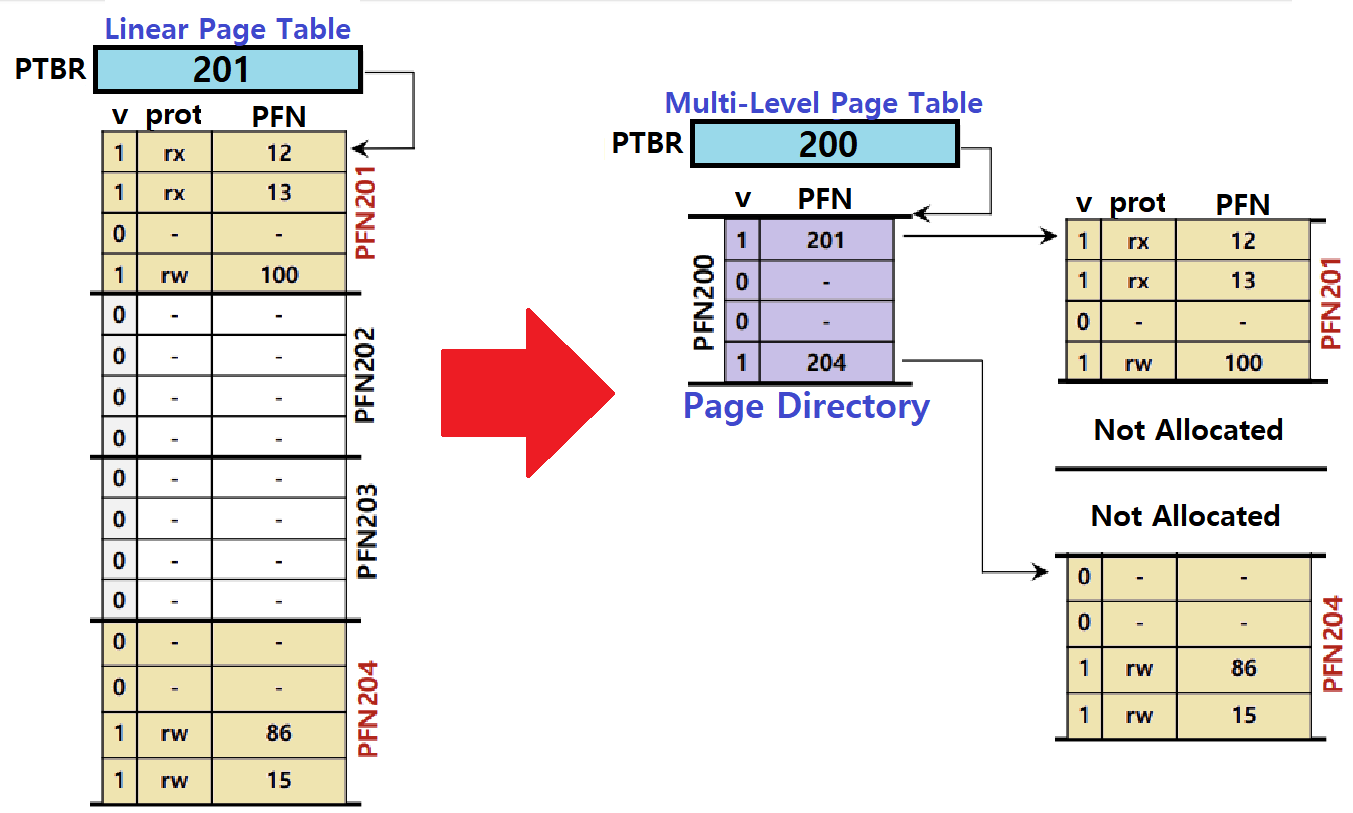
• 좌측은 지금까지 학습한 일반적인 Linear Page Table이다. 16개의 Entry를 가진 Page Table이며, 이 System에서 한 Page(Frame)의 사이즈는 4개 Entry를 포함할 수 있다.

  • 따라서, Linear Page Table은 4개의 '연속적인' Physical Frame들에 마련된다.
    • 이때, 맨 위 4개의 Entry와 맨 아래 4개의 Entry만이 실제 Valid한 VPNtoPFN Translation 정보를 담고 있고, 나머지 Entry들은 Invalid하다.
      • 만약, 이 Page Table을 Frame 단위로 보았을 때, 중간의 두 Frame의 모든 소속 Entry들이 Unused(Invalid)인 것이다.

• 우측은 Multi-Level Page Table이다. 위와 똑같은 상황이라 가정하자.

  • Multi-Level Page Table이기 때문에 Page Directory 자료구조가 새로 도입된다.

    • 한 Page Table은 4개의 Frame으로 나타낼 수 있으니 Page Directory는 총 4개의 Entry를 가지며, 하나의 Frame에 표현할 수 있다. ★★★

  • 이 Page Directory의 한 Entry는 Page Table을 표현하는 한 Frame이 '어떤 Frame인지'를 나타낸다. ★★★

    • 이때, Valid Bit를 두어, 해당 Frame의 Validity를 표현한다. 해당 Frame의 모든 Entry(Translation 정보)가 Unused(Invalid)이면, 해당 Frame 자체가 Invalid가 되어, 실제 Physical Frame으로의 맵핑 정보가 Page Directory에 기입되지 않게 된다. ★★★

이 예시에선, 기존 Linear Page Table에선 Page Table의 표현을 위해 총 4개의 Physical Frame이 쓰였던 것이, Multi-Level Page Table이 되면 총 3개(하나는 Page Directory를 위한 Frame)로 줄어들었음을 알 수 있다. ★

PDE엔 Page Table을 기록하고 있는 Physical Frame의 PFN이 있고, 그 PFN을 따라가서 찾은 Frame의 PTE는 VPNtoPFN Translation 정보가 들어있다. 즉, PFN이 들어있다.

So, we need 'PFN of Page Table Frame', and 'PFN of Frame that we want to access'.

Page Directory의 Entry 개수는 최대 Page 개수만큼 있어야 한다. ★★★

Pros and Cons

  이러한 Multi-Level Page Table은 다음과 같은 장단점을 지닌다.

• Pros

  • 실제로 Process가 사용하는 Address Space만큼만 Page Table Space를 할당한다. ★
    • 즉, 불필요한 Page Table 할당이 사라진다.
  • Page Table의 확장이 용이하다. ★

• Cons

  • 기존 Linear Page Table 방식에 비해 공간 효율은 늘어나지만 Access 횟수가 늘어나기 때문에 시간 효율은 떨어진다. ★★

    • Time-Space Tradeoff

      • 그래서, 이 방식에선 더더욱 TLB Hit 유도가 중요하다. ★

        • TLB Miss인 경우엔 Page Table에서 올바른 Translation 정보를 얻기 위해 두 번의 Memory Loading을 거쳐야 한다. (Page Directory 한 번, Page Table 한 번) ★★★

          • 결론적으론 총 3번의 Access가 일어나겠지?

        • 반면, TLB Hit인 경우엔 성능이 훌륭할 것!

  • 구현이 복잡하다. HW의 도움도 필요하고. ★★

Two-Level Page Table

  조금 더 깊이있게 학습해보자. 아래의 예시를 보자.

• 어떤 System이 있다. 이 System은 다음과 같이 표현할 수 있다.

  • 16KB Address Space를 가진 System이다. Page Size는 64Bytes이다.

    • 16KB=2^14이므로 14Bits로 Logical Address를 표현할 것이다. Page Size에 따라, Offset은 6Bits, 8Bits는 Page 개수가 될 것이다.

  • PTE의 Size가 4Bytes라 가정하면, Linear Page Table 기준 Page Table의 Size는 2^10B = 1KB가 될 것이다.

    • 이때, PTE의 개수는 당연 2^8=256개이다.

      • PTE의 Size는 4Bytes이다. Page Size는 64Bytes이므로, 한 Page엔 16개의 PTE가 들어갈 수 있겠다. ★★★

    • 따라서, Page Table은 16개의 Page로 표현할 수 있다.

      • 그말은 즉슨, PDE의 개수는 16개인 것이다. ★★★
        • PDE의 Size가 4Bytes라 하면, Page Directory의 크기는 16x4Bytes, 즉, 64Bytes로, 하나의 Page에 Fit하게 들어갈 것이다. ★★★★★

  • 이때, 이 System에서 어떤 한 Process의 Page Table이 아래 그림과 같이 구성되었다고 하자.

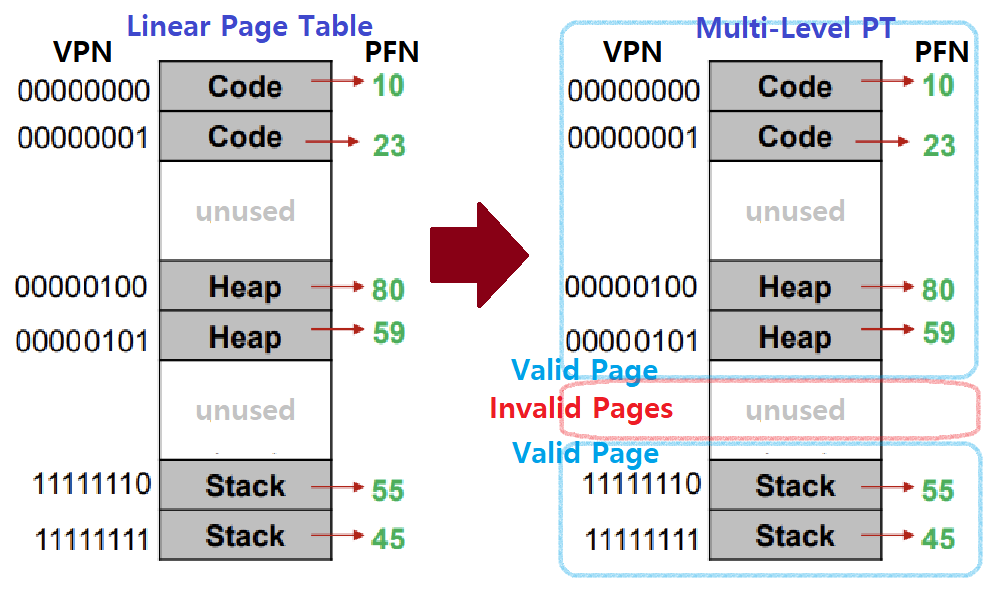
~> 여기서, Multi-Level Page Table 시, 이 Page Table을 위해 필요한 Page의 개수는 몇 개인가?
~~> 그렇다. 단 2개의 Page만 필요하다. Page Size는 64Bytes, 즉, 16개의 Entry를 커버할 수 있는데, Page Table의 5번 PTE까지가 첫 번째 Page에 들어가므로 여기서 하나의 Page가 Valid해진다.
----> 그리고, 같은 논리로, 마지막 Page가 Valid해진다.
----> 그외 나머지, 그 사이의 14개의 Page들은 모조리 Invalid(Unused)할 것이다. ★

따라서, 본 예제에선 Multi-Level Page Table 기준, 총 3개의 Page만으로 Page Table을 구성할 수 있다.

기존 Linear Page Table이었을 경우 16개나 필요했을텐데 말이다! (상당한 효율) ★★★

  위 상황을 약간 더 구체적으로 묘사하면 아래 그림과 같다. Page Directory에 주목해서 보도록 하자.

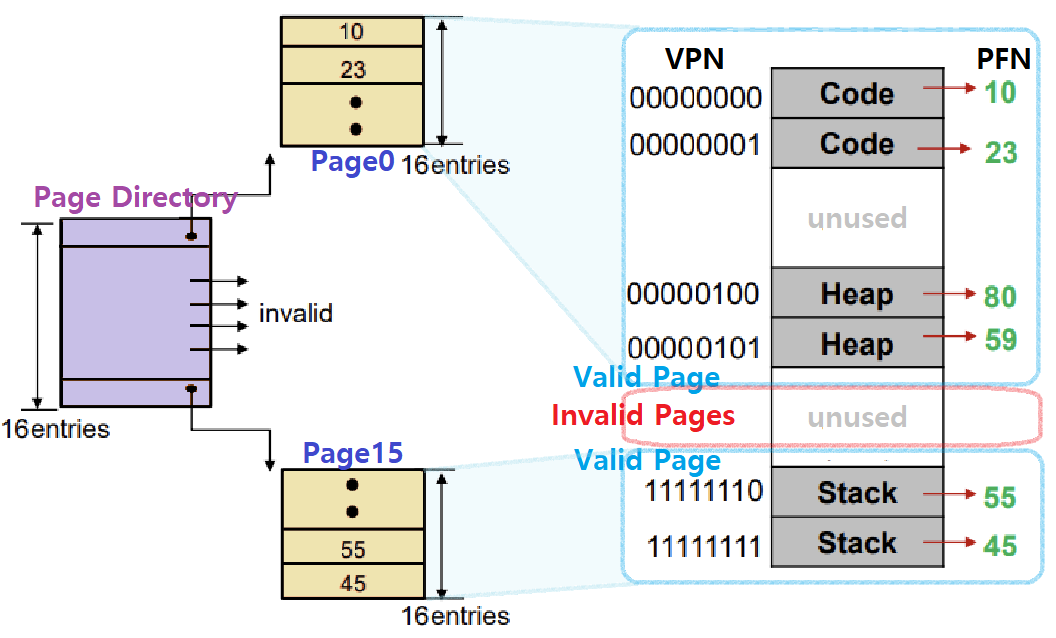
• 이 예시에선 Page Directory가 하나의 Page에 Fit하게 마련될 수 있음을 주목하자. ★

  한편, 이러한 예시에서, 한 가지 궁금증이 들지 않는가?

"그렇다면, Logical Address에 Page Directory Index에 대한 정보가 있어야 하는 것 아닌가요?"

맞다. Page Directory Index를 알아야 한다. 왜냐? 그래야만 PDE가 알려주는 Frame으로 가서 그 Frame에서 Translation 정보를 알 수 있기 때문이다.

따라서, Logical Address Format에 Page Directory Index를 위한 Bits를 마련해야한다.

~> 위 예시에선 PDE의 개수가 16개이므로 4Bits가 Page Directory Index를 위한 공간으로 할당될 것이다.
~~> 따라서, 위 예시 System의 Logical Address Format은 다음과 같아질 것이다.

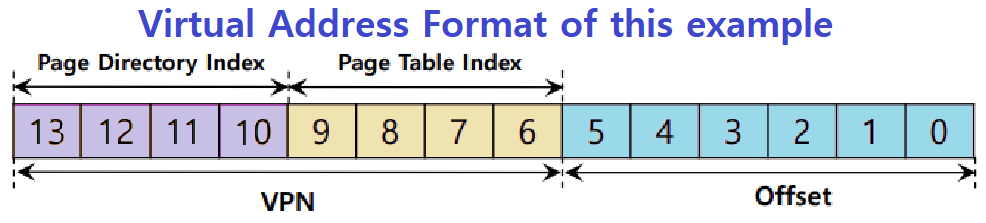
Page Directory Index를 위한 4Bits와 Page Table Index를 위한 4Bits가 모여 VPN을 위한 8Bits가 됨을 주목하라. ★★★★★

2^4 x 2^4 = 2^8이기 때문에, 기존의 Linear Page Table에서의 Logical Page 개수엔 전혀 변함이 없는 것이다. 단지 Level만 바뀐 것이다. ★★★★★

• Page Directory Index (PDIndex)

  • VPN에서 PDE의 Address를 찾는데 사용되는 부분이다.
  • PDEAddr = PageDirBase + (PDIndex x sizeof(PDE))

• Page Table Index (PTIndex)

  • PDE가 가리키는 Valid Page of Page Table에서 PTE의 Address를 찾는데 사용된다.
  • PTEAddr = (PDE.PFN << SHIFT) + (PTIndex x sizeof(PTE)) ★★★
  • PhysAddr = (PTE.PFN << SHIFT) + Offset ★★★

  이 예시의 메모리 구성 상태를 다시 한 번 확인해보면 아래와 같다. 복습해보도록 하자.

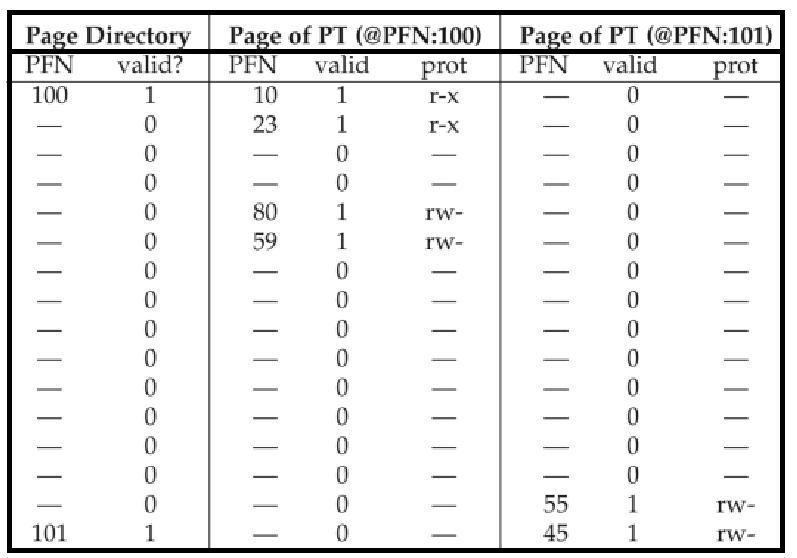
~> 'Single-Level Page Table (Linear Page Table)' 시엔 16개의 Page가 Page Table을 위해 필요했던 것에서, 'Two-Level Page Table'이 되면서 3개의 Page만 필요해졌음을 다시 한 번 강조한다. ★★★

※ 간단한 연습 : Logical Address Space가 1M=2^20인 System이 있다고 하자. Logical Address를 표현하는데에 총 20Bits가 쓰이는 것이다.
~> 이때, Page Size가 1KB라 하면, 총 10Bits가 Offset으로 쓰이겠다.
~~> 나머지 상위 10Bits는 Two-Level Page Table 기준 'PDIndex + PTIndex' 정보이자 VPN 정보가 될 것이다. ★
~> Entry가 4Bytes라 하면, 한 Page엔 2^8=256개의 Entry가 있을 수 있고, 따라서, Page Table의 Entry 개수는 2^10이므로 총 4개의 Frame이 (Linear) Page Table의 구현에 필요하다.
~> 여기서, Page Directory의 구성 상태에 따라 '실제로 필요한 Page의 개수'가 정해질 것이다. (Page Directory는 총 4개의 Entry가 필요하겠지 ★)

Three-Level Page Table

  Multi-Level Page Table에선 Level을 계속해서 추가할 수 있다. 다음과 같은 System을 생각해보자.

• Virtual Address가 30Bits로 구성된다. Page Size는 512Bytes로, Offset에 9Bits, VPN에 21Bits가 필요하겠다.

  • PTE의 크기가 4Bytes라 하면, Page Table의 크기는 2^21 x 2^2B = 8MB가 된다.
    • Page Size가 512B=2^9B이니, 2^9 / 2^2 = 2^7으로, 한 Page 안엔 PTE가 128개씩 들어갈 수 있다.
      • VPN이 21Bits로 표현되니, PTIndex는 7Bits이므로 나머지 14Bits가 PDIndex로 쓰인다.
        • 즉, Page Directory의 Entry 개수는 2^14개이다.
          • Page Directory가 너무 크다. Page Directory를 위해 32개의 Frame이나 필요해진다. ★

• Page Size는 2^9B이고, Page 내엔 2^7개의 Entry가 들어갈 수 있는데,,,

  • 그렇다면, Page Directory에 대해서 Paging을 한 번 더 적용하면 어떤가?
    • 즉, PDE 개수가 2^14개인데, 한 Page엔 PTEorPDE가 2^7개씩 들어갈 수 있으므로, Page Directory를 2^7개의 Page로 쪼개는 것이다. ★★★

즉, 3-Level이 되는 것!

Level이 하나 더 늘더라도 Page에 Entry가 Fit하게 들어가도록 맞춰주자는 것이다. ★

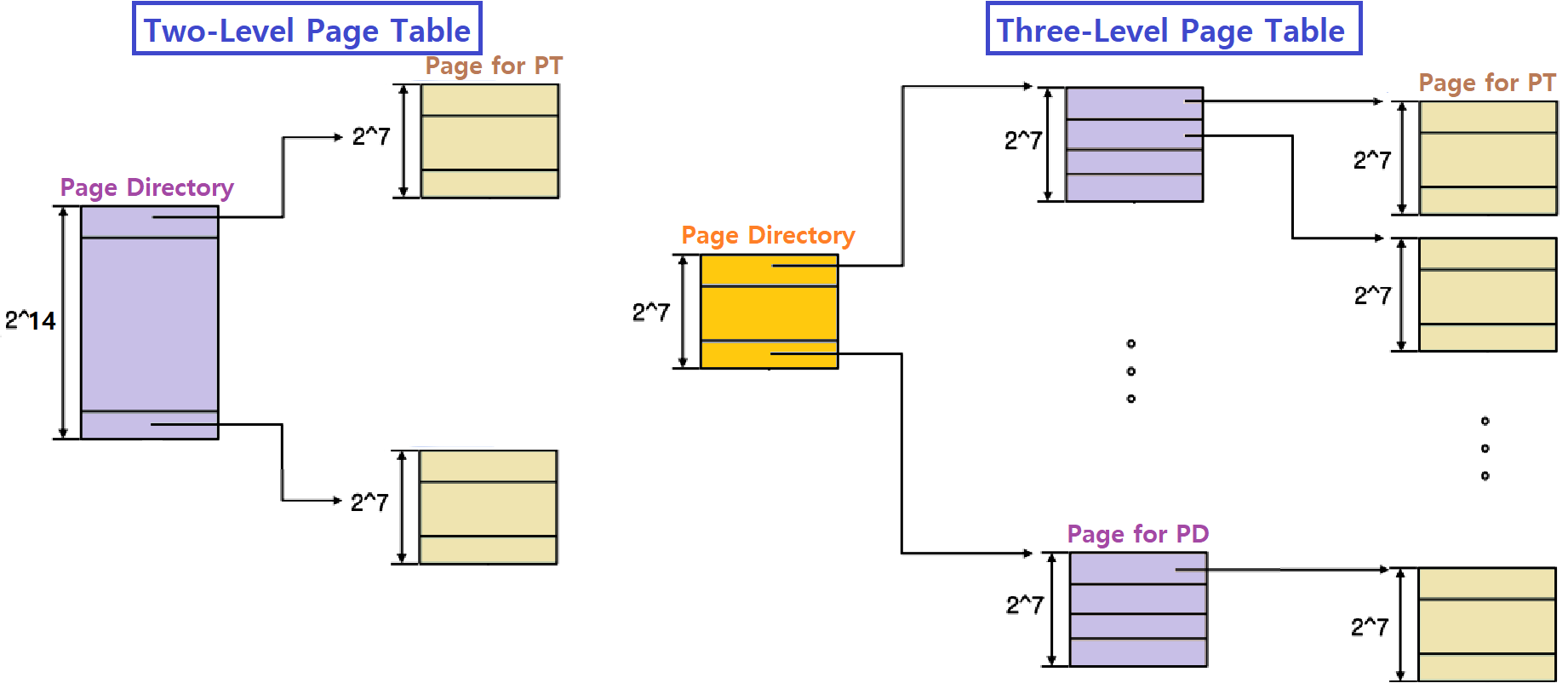
• 위 그림처럼, 3-Level로 Page Table을 구성할 수 있다.
  • 최우측의 Frame들만이 실제 VPNtoPFN Translation 정보가 담긴 Page Table을 구성하고, 나머지 중간, 최좌측 Frame들은 Page Directory 부분이라 할 수 있겠다. ★★

이때, 여기서 Page Table의 Entry가 모두 Valid하다고 할 경우, Total Frame 개수는 몇개일까?

(2^7 x 2^7 + 2^7 + 1)개이다.

(2^7 x 2^7)은 Real Page Table, 2^7은 중간 단계 Page Directory, 1은 Page Directory의 Frame 개수이다. ★★★

기존의 Two-Level Page Table에선 (2^14 + 2^7)개의 Frame이 필요했을 것! 즉, Level을 하나 추가함으로써 Frame이 하나 더 늘어난 것이다. (2^14는 Real Page Table, 2^7은 Page Directory의 Frame 개수) ★★★

이때, Three-Level Page Table에선 Process의 Memory Access 명령 수행 시 총 4번의 Memory Access가 이뤄지는 것이다. ★★★★★

첫번째 PD 1번, 두 번째 PD 1번, PT 1번, 실제 Data의 Frame Access 1번으로 총 4번!

  이 예시에서 Logical Address Format은 아래와 같을 것이다.

Address of PTE (by code)

  이 전체 과정을 코드로 표현하면 다음과 같다. (Two-Level Page Table 기준)

VPN = (vaddr & VPN_MASK) >> SHIFT;
Success = TLB_Lookup(&TlbEntry, VPN);

/* TLB Hit */
if (Success == true) {
	if (CanAccess(TlbEntry.ProtectBits) == true) {
		Offset = vaddr & OFFSET_MASK;
		paddr = (TlbEntry.PFN << SHIFT) | Offset;	// 그냥 TLB Entry 그대로 사용!
		Register = AccessMemory(paddr);
    }
	else RaiseException(PROTECTION_FAULT);
}
/* TLB Miss : It needs 'Full Multi-Level Lookup' */
else {
	PDIndex = (VPN & PD_MASK) >> PD_SHIFT;			// Page Directory Index
	PDEaddr = PDBR + (PDIndex * sizeof(PDE));		// PDE의 Address 계산
	PDE = AccessMemory(PDEaddr);					// PDE 추출

	if (PDE.Valid == false) 						// Valid Page가 없는 곳을
    	RaiseException(SEGMENTATION_FAULT);			// 접근하려하면 SEGFAULT ★★
    else {
		PTIndex = (VPN & PT_MASK) >> PT_SHIFT;		// Page Table Index
		PTEaddr = (PDE.PFN << SHIFT) + (PTIndex * sizeof(PTE));	// PTE 위치 ★★
		PTE = AccessMemory(PTEaddr);							// PTE 추출

		if (PTE.Valid == false) 					// Invalid Entry를 접근하면
			RaiseException(SEGMENTATION_FAULT);		// SEGFAULT ★★
		else if (CanAccess(PTE.ProtectBits) == false)
			RaiseException(PROTECTION_FAULT);
		else {
			TLB_Insert(VPN, PTE.PFN, PTE.ProtectBits); // TLB에 Translation 업데이트
			RetryInstruction();						// Access 재시도!
        }
    }
}

~> 위 코드는 상당히 중요한 정보를 담고 있으니 차분히 분석하도록 하자.
~~> 가장 중요한 부분은 PTE의 주소를 계산하는 부분으로, PDE의 PFN 정보를 Left Shift한 후, Page Table Index를 이용해 '중간 단계 Offset'을 만들어 PTE를 접근하고 있음에 주목하자. 마치 PDE의 PFN이 PTBR Value처럼 작동하는 것이다. ★★★

Exercises

  자, 위에서 학습한 내용을 몇 가지 간단한 예제를 통해 다시 한 번 복습해보자. Logical Address가 64Bits로 표현되고, Page Size는 32KB, PTE Size는 4Bytes인 System을 가정하자. (문제 풀이 간에 Invalid Entry는 없다고 가정)

Question1) Page Offset을 위한 Bits는 몇 개 필요한가?
Answer) 15개
Reason) 32KB = 2^15B이므로 15Bits가 필요하다.

Question2) 각 Page에는 PTE가 최대 몇 개 들어갈 수 있는가?
Answer) 8K개
Reason) Page Size는 32KB, PTE Size는 4Bytes이므로 2^15 / 2^2 = 2^13개 가능하다.
~> 그리고, 이는 곧 PTIndex를 위해 13Bits가 할당될 것임을 암시 ★★★

Question3) 각 Page Table이 Page Boundary에 Fit하게 들어가기 위해선 몇 개의 Level이 필요한가?
Answer) 4 Levels
Reason) 현재 Logical Address 64Bits는 "15(Offset)+13(PTIndex)+36(나머지)"로 구성된다. 이때, 한 Page 안엔 Entry가 총 2^13개씩 가능하다. 나머지 36Bits를 2^13씩 자르면 총 3개의 Page Directory 단계가 발생한다(10 + 13 + 13). 따라서, Page Table을 고려하면 Four-Level Page Table이어야 한다. ★★★
~> Logical Address의 MSB쪽은 10Bits만 둔다. 그래야 맞음. (자명)

Question4) 이 System을 위해 필요한 총 Page의 개수는 얼마인가?
Answer) (1 + 2^10 + 2^10 x 2^13 + 2^10 x 2^13 x 2^13)
Reason) Page Directory를 위 레벨부터 0번, 1번, 2번이라 하면, 0번 PD를 위해선 1개의 Frame이, 1번 PD를 위해선 2^10개의 Frame이, 2번 PD를 위해선 2^10 x 2^13개의 Frame이 필요하며, Page Table을 위해선 2^10 x 2^13 x ^13개의 Frame이 필요하다. 따라서 총 Frame 개수는 (1 + 2^10 + 2^10 x 2^13 + 2^10 x 2^13 x 2^13)개이다. ★★★★★

Question5) 이 Page Table은 총 몇 개의 Frame을 Address할 수 있는가?
Answer) 2^49개
Reason) Q4와의 차이점을 명확히 인지하자. 이 Page Table을 '위한' Frame의 개수와, 이 Page Table이 '접근할 수 있는' Frame의 개수는 엄연히 다른 이야기이다. 이 Page Table의 총 Entry 개수를 보면 되는데, 이 System의 Logical Address에서 VPN이 총 몇 Bits인지 보면 된다. 그렇다 49Bits이다. 이는 즉슨, Process VAS의 총 Page 개수가 2^49개임을 의미하고, 이것이 곧 Address할 수 있는 Frame의 개수와 같다. ★★★

Question6) Page Table의 Size는 얼마인가? (Byte 단위로)
Answer) (1 + 2^10 + 2^10 x 2^13 + 2^10 x 2^13 x 2^13) x 2^15
Reason) 이는 Q4를 그대로 이용하면 된다. 이 Page Table을 구축하기 위한 Frame의 개수는 (1 + 2^10 + 2^10 x 2^13 + 2^10 x 2^13 x 2^13)이다. 여기에 Frame(Page) Size인 2^15를 곱해주면 되겠다. ★★★
~> Linear Page Table의 Size와 구분하도록 하자! ★★★★

Question7) 이 System에서 특정 Page를 Address하기 위해 필요한 Memory Access 횟수는 얼마인가?
Answer) 5번
Reason) 쉽다. 0번 PD, 1번 PD, 2번 PD, PT, 진짜 접근하려는 Page, 이렇게 총 5번의 Memory Access가 필요하다.

Inverted Page Table

  여태 설명한 것이 일반적인 Page Table 구축 방법론이라면, 이 'Inverted Page Table'은 특별한 구축 방법이다.

Inverted Page Table : Physical Memory의 각 Page에 어떤 Process가 올라가는지를 특정 Table로 관리해서 지정해주자!

즉, 방향이 바뀐 것이다. ★

• 이 '특정 Table'에는,

  • 한 Entry가 Memory의 한 Page에 대응한다.

  • 각 Entry에는 Page의 실제 저장 위치에 대한 Virtual Address가 저장되어 있다.

    • 그리고, 그 Page가 어떤 Process의 Page인지를 pid나 ASID 등을 추가로 기록해서 나타낸다. ★

  • 각 Process의 Page Table을 저장하기 위한 메모리가 줄어든다. 필요한 Page만 올리면 되기 때문!

  • 허나, Page Reference를 위한 Table Search가 필요하기 때문에 시간 효율이 떨어진다.

    • 이를 개선하기 위해 Hash를 쓰곤 한다.

  • 일부 OS에서 실제로 운용하는 방식이다.

즉, Logical Address에 Process에 대한 정보도 함께 둔다고 생각하면 된다. ★

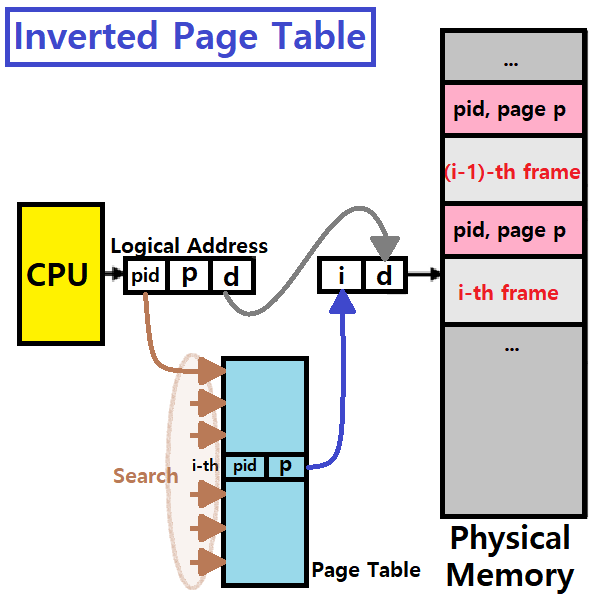
• Inverted Page Table의 Size는 어떻게 알 수 있을까?
  • Page Size가 1K, Physical Memory가 1M라 하자.
    • 2^20 / 2^10 = 2^10. 즉, 2^10개의 Frame이 있고, 이는 곧 Inverted Page Table에 2^10개의 Entry가 필요함을 의미한다.
      • Entry가 4Bytes이면 Page Table의 크기는 4KB가 되겠다. ★
        • 기존 Multi-Level Page Table보다 Page Table의 Size는 훨씬 더 줄어든다. ★★

  금일 포스팅은 여기까지이다.

+PS at 13/01/23) 현재 Velog 주인장 본인의 연구실 활동으로 인해 OS 연재를 마무리할 여력이 없어 당분간(또는 영원히..?) OS 연재는 멈추겠습니다. 지난 학기 OS 기말고사 + PintOS Project 후반 Phase가 겹쳐서 작년 11월부터 연재를 못하고 있었는데, 방학 때 마무리할 계획이었으나 현재는 연구실 활동에 전념할 시기라 판단되어 (제 스스로에 대한 약속이었는데 지키지 못해) 안타깝지만 연재를 멈추겠습니다. 저 역시 아직 OS에 대해 모르는 부분이 많고, 본 연재에 부족한 내용도 일부 있을 수 있기에 본 연재가 참조하는 교재인 OSTEP을 열심히 봐주시길 바랍니다. 저도 틈날때마다 계속 공부하겠습니다.