SP - 5.6 Thread-Level Parallelism

Modern Days CPU

  지금까지 우리는 Critical Section에 대한 Mutual Exclusion을 제공해 Synchronization 문제를 해결했었다. 그 과정에서, 프로그램이 돌아가는 기반 컴퓨터가 단일 CPU인지, Multicore인지는 고려하지 않았었다.

  허나, 알다시피 현대 컴퓨터는 대부분 Multicore CPU를 탑재하고 있다. Single Chip에 여러 CPU Core를 넣어놓은 것이다.

  한편, 현대 컴퓨터에선 Hyperthreading 개념도 등장한다. 여러 개의 Instruction Stream들이 하드웨어를 공유할 수 있게 하는 개념이다. load/store/add 등의 HW 연산들이 하나가 아닌 여러 HW를 동시에 사용할 수 있게 해준다. 어떻게? Register Set과 Program Counter 등을 여럿 둠으로써 말이다.

  예를 들어, 4 Core CPU에 특정 Hyperthreading(ex. 2배로 만들어주는)을 적용하면, 마치 8개의 CPU가 있는 것처럼 동작할 수 있는 것이다. 마치 8개의 Core가 있는 것처럼 말이다.

• Multicore & Hyperthreaded CPU가 주는 이점

  • Thread 위에 Work를 분배함으로써 실제로 Parallel Execution이 일어나게 할 수 있다.

    • 자동으로 이런 분배 행위가 일어난다.
      • 예를 들어, 다양한 APP을 동시에 돌리거나, 복수의 Client에게 Service를 제공하거나 하는 식으로!

  • 나아가, Big Task를 Sub Tasks로 쪼개고, 이들을 Multiple Parallel Threads에 부여함으로써, 수행 속도 향상을 도모할 수 있다.

Typical Multicore Processor

  Thread에는 가능하면 최대한 Independent Task들을 부여해 '동시 수행' 이루어지도록 유도해야한다. 그래야 현대 Multicore System에서 이를 '진짜로' Parallel하게 수행할 수 있기 때문이다.

"그러나, 일반적으로 Thread들이 공유하는 자료구조가 있기 때문에 '완벽하게' Parallel하게 동작하기란 쉽지 않다."

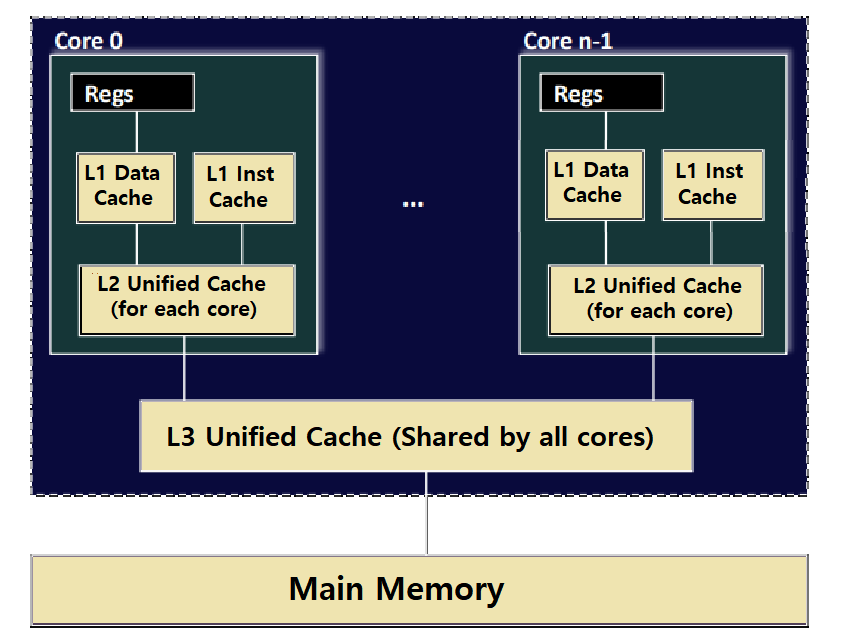
• 위의 그림을 보자. 'Typical Multicore Processor'의 구조이다. 4개의 Core로 이루어져 있다고 가정하자.

  • 각 Core 안에는 복수의 Cache Memory가 존재한다.

  • 그리고, CPU(Core)들이 들어있는 Chip이 Main Memory와 연결되어 있다.

• Cache들은 L1, L2, L3의 Level로 구분된다.

  • 이 중, L1과 L2 Cache는 'Private Cache'로, 각 Core에 대해 하나씩 존재하고, 자기 자신(Core)들만 해당 Cache에 접근할 수 있다. ★

    • 즉, Core 0은 Core 1의 L1, L2 Cache에 접근할 수 없다.

  • 반면, L3 Cache는 'Shared Cache'로, 모든 Core가 Share한다. ★

• L1 Cache는 Data Cache와 Instruction Cache로 구분되고, L2, L3 Cache는 Unified Cache이다.

• 알다시피, 일반적으로 Main Memory는 DRAM으로, Cache Memory는 SRAM으로 만들며, Register Set에 가까울수록 수행 속도가 빠른 특성이 있다.

  • 즉, DRAM(Main Memory)이 가장 느리고, Register를 제외하고 보면, L1 Cache가 가장 빠른 것이다.
    • 수행 속도가 빠르다는 것은 Latency가 짧다는 의미이다. ★★★

이 L1, L2, L3 Cache 관계는, Core가 Data를 찾을 때, 처음에 Register에서 찾고, 없으면 L1 Cache에서 찾고, 없으면 L2 Cache에서 찾고, 없으면 L3 Cache에서 찾고, 여기까지도 없으면 Main Memory에서 Data를 찾는 식으로 진행됨을 의미한다. ★

Thread-Level Parallelism

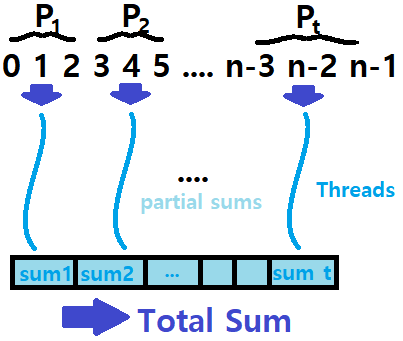
Parallel Summation Example

  위의 'Typical Multicore Processor' 구조를 염두한채로, 'Parallel Summation' 예제를 보자.

• 0부터 n-1까지의 값을 더하는 굉장히 간단한 프로그램을 만들어보자.

  • 결과는 당연히 공식에 따라 ((n-1)*n)/2일 것이다.

• 우리가 Multicore Processor를 이용해 Parallel Programming을 하기 위해선, 0부터 n-1까지의 수를 Partitioning해야한다.

  • 0부터 n-1까지를 특정 Range t를 기준으로 구분해, 각 조각을 Thread들에 할당하고자 하는 것이다.

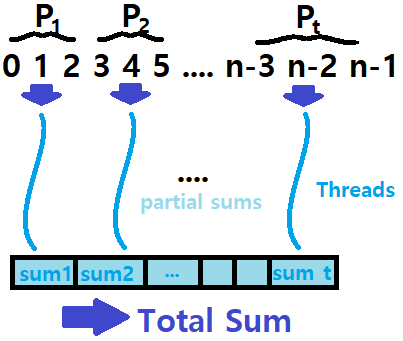
• n개의 수(0 ~ n-1)를 t로 나누니, 각 Partition에는 Flooring(n/t)만큼의 수들이 들어있을 것이다.

  • 이러한 t개의 Partition에 대해 t개의 Threads를 할당해, 각 Thread가 각 Partition Range를 Summation하도록 처리하는 것이다.

  • 분석의 편의를 위해, n이 t의 배수에 해당하는 값이라 하자.

Q) 굳이 이렇게 덧셈을 해야하나요?
A) Multicore Processor를 이용한 Parallel Programming을 이해하기 가장 쉬운 예시가 바로 이 예시이다. 따라서, 실제로는 유용한 프로그램은 당연 아니다.

• 이 예시 프로그램을 돌리는 Machine을 가정하자. 본 포스팅의 참조 교재에서는 다음과 같은 스펙의 Machine을 언급한다.
  • 8 Cores
  • Each core can do 2x Hyperthreading
    • 그렇다. 이 PC는 마치 16개의 Core가 있는 수준의 성능을 보일 것이다.

Bad Implementation - Mutex

  이러한 'Parallel Summation Thread Program'을 구현하는 방법은 무엇이 있을까? 처음 시도해볼 수 있는 방법은, Thread들이 각자의 부분 합을 Global Variable에 업데이트하되, Semaphore를 적용해 Synchronization을 시키는 방법이다.

• 여태 다루었던 개념을 그대로 적용한 것이다. 가장 Naive한 방법이라 볼 수 있다.
  • Thread를 여럿 띄우고, 각 Thread가 gsum이라는 Global Shared Variable을 Update하는 방식이다. Mutex를 입혀서 말이다.
    • 모든 Thread의 수행이 끝나면, 우리가 원하는 0 + 1 + ... + n-1의 결과가 gsum에 저장되어 있을 것이다.

• 모든 Threads가 Global Variable을 접근하기 위해선 Mutex를 잡아야 한다.

  • 즉, 모든 Threads의 접근이 직렬화된다. ★★★

  • Critical Section은 안전하게 보호되지만, 동시에 Cost가 높아지는 것이다. ★★

    • 왜냐? 쉽게 생각해보자. Thread들이 동시에 접근하지 않고, 일일이 줄을 서서 자기 차례를 기다린 다음, 변수에 접근하지 않는가. 따라서, Mutex의 사용은 이 상황에선 Cost가 높은 것이다.

void *sum_mutex(void *vargp); 		// Thread Routine
long gsum = 0; 						// Global Shared Variable for Summation
long nelems_per_thread; 			// 각 Thread에서 합할 Elements의 개수!
sem_t mutex; 						// gsum을 Protect할 Binary Semaphore

int main(int argc, char **argv) {
	long i, nelems, log_nelems, nthreads, myid[MAXTHREADS];
	pthread_t tid[MAXTHREADS];

	nthreads = atoi(argv[1]);				// t
	log_nelems = atoi(argv[2]);				// n
	nelems = (1L << log_nelems);			// 0부터 2^n까지 더할 것(2^n = N)
	nelems_per_thread = nelems / nthreads;	// 더할 Elem 개수, Flooring(N/t)
	sem_init(&mutex, 0, 1);					// Binary Semaphore

	for (i = 0; i < nthreads; i++) {
		myid[i] = i; 
		Pthread_create(&tid[i], NULL, sum_mutex, &myid[i]); // Thread를 띄움
	}
	for (i = 0; i < nthreads; i++)
		Pthread_join(tid[i], NULL); // Reaping Routine

	if (gsum != (nelems * (nelems-1))/2)
		printf("Error: result=%ld\n", gsum); // Sum이 제대로 이루어졌는지 확인

	exit(0);
}

/* Thread Routine */
void *sum_mutex(void *vargp) {
	long myid = *((long *)vargp); 			// 몇 번 Thread인지 기록
	long start = myid * nelems_per_thread; 	// 이 Thread의 Range의 시작 숫자
	long end = start + nelems_per_thread;	// 이 Thread의 Range의 끝 숫자
	long i;

	for (i = start; i < end; i++) { 		// 쭉 더한다.
		P(&mutex); 
		gsum += i; 							// Critical Section 보호하면서!
		V(&mutex); 
	}
		
	return NULL;
}

• 교재에 따르면, 0부터 2^31까지 더하도록 프로그램을 수행 했을 때, Thread 개수(이용하는 Core 개수)에 따라 다음과 같은 결과가 출력되었다고 한다.
  • Thread 개수는 곧 Core 개수이다. 왜냐? Parallel Program이므로! 현재 가정 Machine이 총 16개의 Core가 있는 것처럼 수행할 수 있기 때문에, Thread 개수가 16개일 때까지는 모든 Thread가 동시에 수행할 수 있는 것이고, 따라서 Thread 개수를 Core 개수라고 보는 것임.

결과 : Thread가 늘어났는데, 예상과 다르게 오히려 성능이 더 안좋아졌다. ★★★

즉, Mutex를 이용하더라도, (Shared Data Structure를 접근하는) Thread들을 사용하는 Thread Program은 Parallel Execution의 이득을 전혀 보지 못하는 것이다. 오히려, Thread 개수가 늘어날수록 경쟁이 더 심해져 더 느려질 뿐이다. ★★★★★

• 기본적으로 1개의 Thread로 프로그램을 돌렸을 때 51초가 걸렸으니, 이도 매우매우 느린 속도인데, Thread 개수가 늘어나면 오히려 더 느려지는 것이다.
  • 상당히 놀랍고 신기한 사실이다.

Good Implementation - Array

  앞선 Implementation에서, Threads가 Shared Data Structure를 접근토록 하니 아무리 Mutex를 사용하더라도('아무리'라는 Wording이 적절치 않을 수 있다) 속도가 더 느려지는 것을 본 바 있다.

  여기서 Idea를 얻어, gsum이라는 Shared Data Structure를 두지 말고, 하나의 Array를 두어, 각 Array Element가 각 Thread에 1대1 대응하게 만들어, Partial Sum을 Array Element에 두는 방식을 생각해보자.

~> Mutex를 사용할 필요 자체를 없애는 것이다.
=> Thread들이 Mutex를 잡기 위해 Contending하는 작업 자체를 사라지게 하는 것이다. ★★★

• Peer Thread i가 psum이라는 Global Array의 Element psum[i]에 Partial Sum을 기록하게 만드는 것이다.
  • Main Thread는 모든 Peer Threads의 종료를 기다리고, 종료되면 psum elements들을 모두 더하는 것이다.
    • Mutex Synchronization이 사라지는 것이다.

#define MAX_NUM		10000000
// ...
long psum[MAX_NUM];
// ...

/* Same Main Routine as previous example */
// ...

/* Thread Routine */
void *sum_array(void *vargp) { 
	long myid = *((long *)vargp);
	long start = myid * nelems_per_thread;
	long end = start + nelems_per_thread;
	long i; 

	for (i = start; i < end; i++) 
		psum[myid] += i; 				// Thread 각자가 자신의 Element에 Sum!

	return NULL; 
}

• 앞선 예제에서처럼, Threads를 최대 16개까지 띄워가며 실험해본다. 교재에 따르면 결과는 다음의 그래프와 같다.

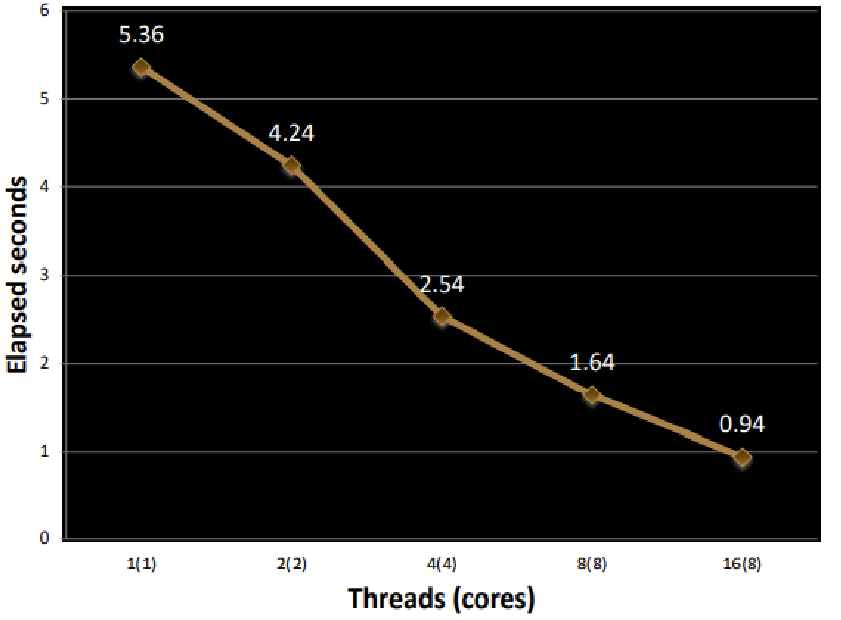
결과 : 드디어 Parallel Execution의 효과를 보고 있다. 예상대로, Threads가 많아질수록 프로그램의 수행 속도가 더 빨라지고 있다. 단일 CPU(Thread가 하나)일 때도, 이전 방식에 비해서 훨씬 효율적임을 알 수 있다.

즉, 아무리 Threads를 이용해 Multicore System 상에서 Parallel Execution을 도모하더라도, Threads가 Shared Data Structure를 다같이 접근하는 구조이면 오히려 프로그램 수행 속도가 느려진다는 것을 알 수 있다. ★★★

Mutex를 사용하지 않으면 속도가 빠를 것이다. 그런데, 알다시피 Mutex를 사용하지 않으면 Corruption이 일어날 것이다. ★★★★★

Great Implementation - Array with local

  Computer Architecture에 대한 이해 수준이 높은 프로그래머라면(사실 수준이 높지 않아도), 위의 Array Implementation에서 한 가지 개선할 수 있는 부분이 있다는 것을 눈치챌 것이다. 아래 코드에서 개선 지점을 찾아보자.

for (i = start; i < end; i++) { 
	psum[myid] += i;
}

~> 그렇다! Indexing을 통한 Memory Reference가 계속 이뤄지고 있다.
=> Array 크기가 작으면 상관 없겠지만, Array 크기가 크면, Array[i]의 실제 저장 위치가 Main Memory가 아닐수도 있다(Cache는 고려하지 말자).
--> 만약, Array[i]의 Virtual Memory Address의 Mapped Physical Memory Address가 Main Memory(or Cache)가 아니라, Disk이면 어쩔 것인가? 디스크가 아니라 메인 메모리여도 문제이다. DRAM 접근 속도는 SRAM 접근 속도보다 10배 가량 느리다. 디스크는 훨씬 더(약 1만배) 느리고.
----> Array Size가 크면 클수록 Memory Accessing Overhead가 발생할 확률이 높아진다. ★★★

"그렇다. Iteration 내에서 Array Element에 접근하지 말고, Thread Routine 내에 Temporary Summation Variable을 하나 마련하고, 거기다 Partial Sum을 수행한 다음에, 최종적인 Sum 결과만 Array Element에 넣으면 되지 않을까?"

  이 점을 고려하여, 아래와 같이 Thread Routine을 개선할 수 있다.

/* Thread Routine */
void *sum_local(void *vargp) {
	long myid = *((long *)vargp);
	long start = myid * nelems_per_thread;
	long end = start + nelems_per_thread;
	long i, sum = 0;

	for (i = start; i < end; i++)  
		sum += i; 
        
	psum[myid] = sum;
    
	return NULL;
}

• 교재에 따르면, 위와 같이 개선할 경우, 수행 속도는 아래 그래프와 같이 더더욱 향상된다고 한다.

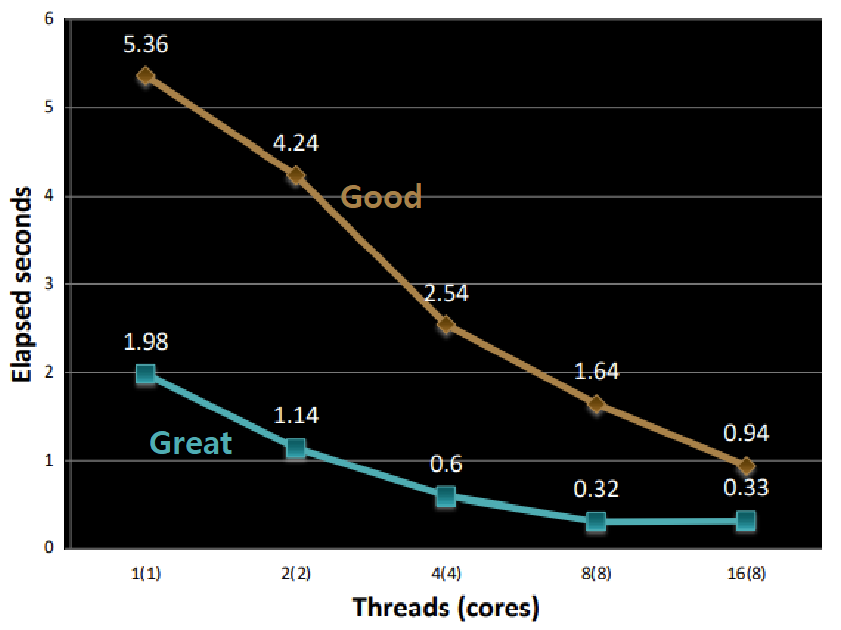
Performance Evaluation

  우리는 앞선 Parallel Summation 예제를 통해 Thread-Level Parallelism의 장점을 확인했다. 이번엔, 이러한 Parallel Program의 성능을 평가하는 방법에 대해 알아보자.

Measure Parameters

  아래와 같이 몇 가지 측정 파라미터들이 있다. Tk는 k개 Core를 이용해 프로그램을 수행한 Running Time을 의미한다. k개의 Thread를 띄운 것이라 생각하면 된다.

• Speedup : Sp = T1 / Tp
  • Thread(Core) 하나로 프로그램을 수행했을 때보다 Thread(Core) 여러 개로 프로그램을 수행할 때가 더 성능이 좋을 것이다(잘 만든 Parallel Program이라면).
    • 따라서, T1을 Tp로 나누어, 얼마만큼 속도 향상이 이뤄졌는지를 판단하는 것이다. 이를 Sp라고 한다.

• Relative Speedup : T1이 Parallel Version of Code일 때 (Core는 하나)

• Absolute Speedup : T1이 Sequential Version of Code일 때 (Core는 하나) ★

  • 보통, '절대 Speedup'을 기준으로 판단한다.
    • 그래야 Parallelism의 이점을 파악하기가 더 편하기 때문이다.

• Efficiency : Ep = Sp / p = T1 / pTp

  • Speedup을 p로 나눈 값이 Efficiency이다. 여기서 p는 Core의 개수를 말한다. ★

    • 이 수치는 Parallelism으로 인해 발생하는 Overhead를 측정할 때 유용하다. ★

    • 0초과 100이하의 Percentage 값으로 표현한다.

Ex) T1이 1, T4가 0.25라 해보자. S4는 1/0.25로 4이고, E4는 4/4=1 (100%)이다. 즉, Parallelism을 통해 속도는 4배 향상시켰는데, 그로 인한 Overhead는 없는 것이다. 매우 잘 된 병렬처리인 것이다.

Ex) T1이 1, T4가 0.5라 해보자. S4는 1/0.5로 2이고, E4는 2/4=0.5 (50%)이다. 즉, 50%의 손실이 생겼다는 뜻이다. Parallelism을 통해 속도 향상을 도모했지만, '가장 이상적인 향상'에 비했을 땐 50%의 손실이 발생했다는 것이다. ★★★

Example) Parallel Summation - Great.Ver

  앞선 Parallel Summation의 세 번째 Implementation에 대해 위의 측정 방법을 적용해보자. 교재에 따르면 그 결과는 아래 표와 같다.

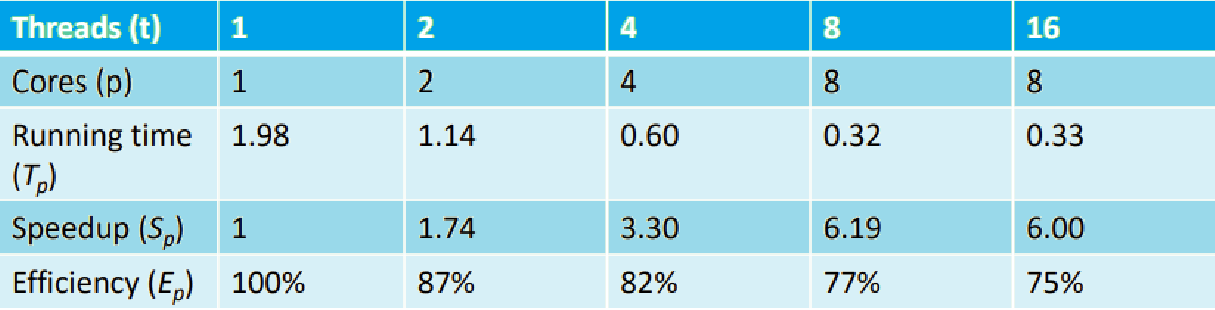
• Core는 최대 8개까지인데(앞서 언급) Hyperthreading을 통해 Threads는 16개까지 띄우고 있음을 기억하자.

• Core(Thread)가 하나일 때의 T1가 1.98이다.

• Core(Thread)가 두 개일 때의 T2는 1.14이다.

  • S2 = 1.98 / 1.14 = 1.74 (근사치)이다.
    • E2 = S2 / 2 = 0.87
      • 87%의 효율을 보였다. 즉, 13%의 손실을 본 것이다.
        • 효율성은 준수하다. 훌륭한 수준은 아니지만.

• 가면 갈수록 Running Time도 빨라지고 Speedup도 계속 올라가고 있지만, 동시에 Efficiency는 가면 갈수록 안좋아지고 있다.

  • 결국 Threads가 16개인 순간에는 Running Time, Sp가 오히려 더 떨어졌음을 알 수 있다.

• 통념상, Core/Thread 개수가 늘어날수록(Shared Data Structure 없이 '잘' Parallelism을 적용했을때) Speedup이 계속될 것만 같지만, 그렇지 않은 것이다.

  • Threads가 늘어날수록 성능이 좋아지다가, 어느 순간 Speedup이 꺾이는 지점이 있다. ★★★
    • 이 예시에서는 Threads(Cores)가 8개일 때가 가장 Best이다.

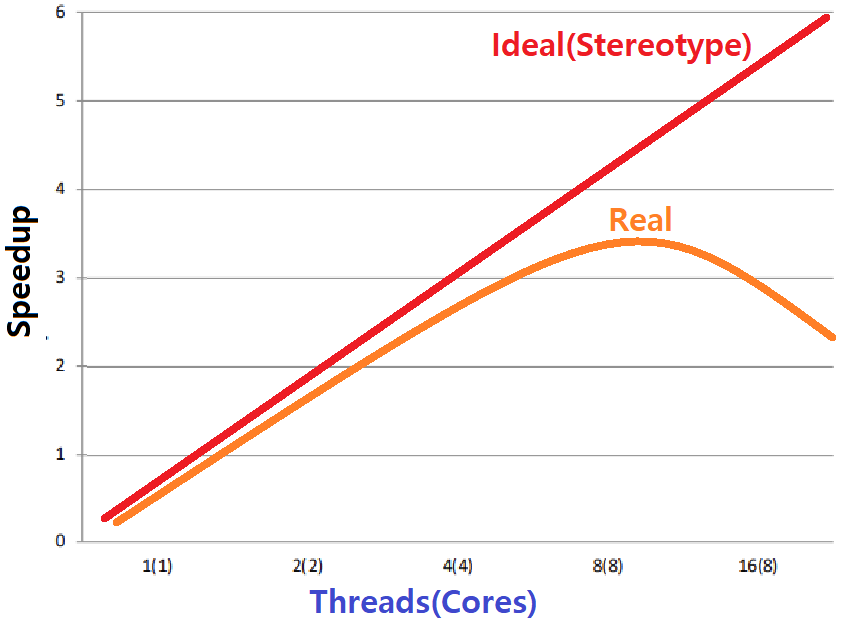
~> 이유가 무엇일까? 이에 대한 해답은 바로 아래 Part에서 구체화할 수 있다.

Multicore Overheads

Memory Consistency

  아래 그림을 보자. 메모리에 변수가 두 개 있다. 둘 다 int type이며, 변수 a의 값은 1, 변수 b의 값은 100이다. Thread1은 a라는 변수를 2로 바꾸고, b 변수를 읽어서 프린트한다. Thread2는 b라는 변수를 200으로 바꾸고, a를 읽어서 프린트한다.

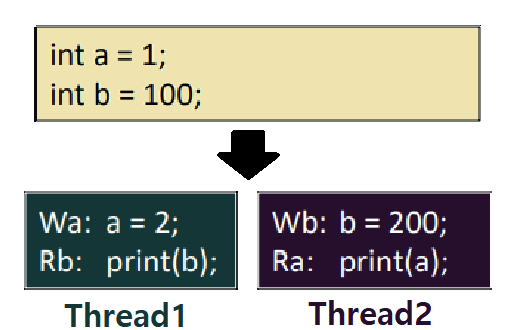
• 이때, 이 둘을 동시에 수행시키면, Interleaving이 가능하기 때문에 Print 결과가 Non-Deterministic하리란 것을 우리는 이미 알고 있다.
  • 이처럼, Thread Program의 Result는 HW 구조 및 동작에 따라 달라지기 때문에 미리 예측할 수 없는 현상을 'Memory Consistency'라 한다.

    Memory Consistency : Thread Program의 Result가 Memory Consistency Model에 의존하는 현상

Sequential Consistency

  한편, 현재 예시 상황에서 Thread1과 Thread2의 실행 순서 자체는 바꿀 수 없다. 두 Thread의 Execution Order는 이미 Fixed이다.

• Thread1 : Write_a -> Read_b

• Thread2 : Write_b -> Read_a

• 이를 고려한 채, 가능한 Sequence를 따져보면 다음과 같다(Write_a = Wa, Read_a = Ra와 같이 Notation을 사용한다. 그리고 Wa는 a를 2로 만들고, Wb는 b를 200으로 만든다).

  • Wa - Rb - Wb - Ra

    • 이 Sequence로 흐르면 출력 결과는 a = 2, b = 100

  • Wa - Wb - Ra - Rb

    • 이 Sequence로 흐르면 출력 결과는 a = 2, b = 200

  • Wa - Wb - Rb - Ra

    • 이 Sequence로 흐르면 출력 결과는 a = 2, b = 200

  • Wb - Ra - Wa - Rb

    • 이 Sequence로 흐르면 출력 결과는 a = 1, b = 200

  • Wb - Wa - Ra - Rb

    • 이 Sequence로 흐르면 출력 결과는 a = 2, b = 200

  • Wb - Wa - Rb - Ra

    • 이 Sequence로 흐르면 출력 결과는 a = 2, b = 200

  • 보면 알 수 있다시피, a = 1, b = 100이란 출력 결과는 불가능하다.

    • 이런 현상이 바로 Sequential Consistency이다.

      Thread Program의 Result가 각 Thread의 개별적인 Sequential Execution Order에 종속적이고, 이에 따라 Interleaving 상태가 결정되는 현상을 의미한다.

      Memory Consistency Model 중 하나이다.

Snoopy Cache

  Computer Architecture를 학습해본 경험을 떠올려보자. Cache Memory에서의 Write-Through, Write-Back Mechanism에 대해 배운 바 있을 것이다. 만약, 위의 Thread Program 예시에서, Cache의 Write-Back도 고려해야 한다면 어떤 느낌이 오는가?

  그렇다. 심란할 것이다. Thread Program을 분석할 때, Cache까지 고려하기 시작하면 더더욱 어려워진다. 하지만, 어렵다고 해서 그냥 넘어갈 순 없다. 아래를 보자.

• Cache가 있다는 것은 Main Memory의 Data에 대한 Copy가 Cache에 있음을 의미한다.

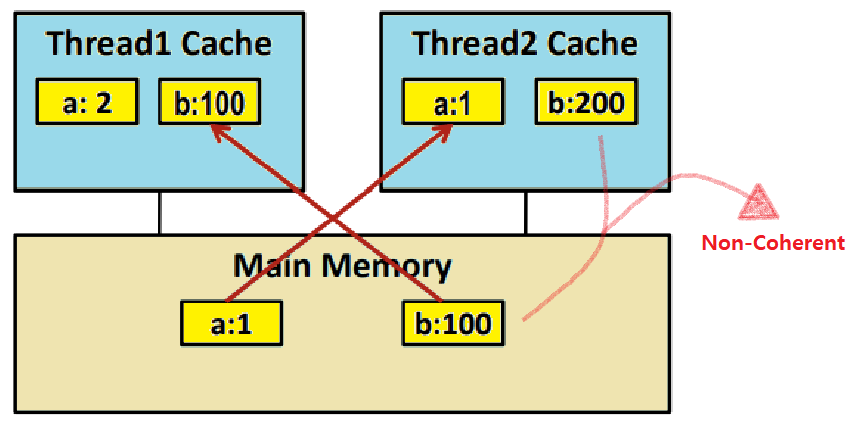
  • 이를 염두한 채, 위의 Thread Program에서, Thread1의 Wa와 Thread2의 Wb가 연달아 수행된 시점을 생각해보자. 이어서 Thread1의 Rb가 수행되려고 하는 상황이다.

    • T2의 Wb로 인해 변수 b가 200으로 업데이트되어 있다.

    • Thread2(Core2)의 L1 Cache에는 'b=200;' 명령이 수행되면서 b 변수를 저장하게 된다.

      • 따라서, Thread2의 L1 Cache에는 'b가 200으로 업데이트되었다는 사실'이 기록되어 있다(Thread2에서 b=200 명령 수행 시 load를 L1 Cache에서 했을 것이므로 ★★).

    • 하지만, Cache는 Write-Back Mechanism을 사용하므로, 'b가 200으로 업데이트되었음'이 아직 Main Memory에는 알려지지 않은 시점이 있을 것이고, 이 시점을 생각해보자.

    • Thread1에서 Read_b를 하려고 하는데, Thread1(Core1)에선 b 접근을 처음하므로 Main Memory에서 Fetch할 것이다.

      • 그런데, DRAM(Main Memory)의 b 값은 '이전의 100'이다.

    Parallelism에선 이러한 'Cache-Main Memory 최신화 문제'가 존재한다. ★

    이러한 예시 상황을 'Non-Coherent Cache Scenario'라고 한다.

"Non-Coherent Cache 문제를 어떻게 해결할 수 있을까?"
~> Snoopy Cache 개념을 도입한다!

• Snoopy Cache : Cache의 각 Block에 State를 나타내는 Tag를 붙인다.

  • Tag의 종류는 다음과 같다.

    • Exclusive : Writable Copy
      • Default Tag로, Modify가 가능한 Data Block이다. 먼저 Modify를 하는 Cache가 독점적으로 그 Data의 '최초 변경자'가 될 수 있기 때문에 Exclusive라고 부른다.
    • Shared : Readable Copy
    • Invalid : Cannot use value
      • 특정 Cache에서 Data A에 대해 Modify하면, Data A를 가지고 있는 모든 Cache에서 Data A가 있는 E-Tagged Block은 Invalid Tag가 붙는다. 쓸 수 없는 것이다. 대신, 최초 변경한 Cache의 Data A Block은 Invalid가 아니라 Shared가 되어, 다른 Cache에서 Read할 수 있게 된다.

  • 이런 매커니즘이 HW적으로 구현되어 있다(Bus Snooping).

Summary : Multicore Processor는 이처럼 Sequential Consistency, Snoopy Cache 등의 개념을 실현시키기 위해 내부적인, HW적인 Overhead가 불가피하다. ★★

그리고 이러한 Overhead는 Multicore Processor 위에서 Thread Program을 돌릴 때 어느 순간 변곡점이 발생하는 원인 중 하나로 꼽힌다. ★★★★

  Thread에 대한 포스팅은 여기까지 한다. 많은 길을 달려왔다. 이제는 Thread가 무엇인지 나름 자신있게 설명할 수 있을 것이다. 보다 더 심화된 Thread 및 관련 Computer Science 개념은 추후 OS 시리즈를 제작할 때 다뤄보도록 하겠다.