정의
그래프
그래프(Graph)는 연결되어 있는 데이터들의 관계를 표현하는 자료구조이다. 다양한 형태를 가질 수 있는 여러개의 노드(Node)와 노드 사이를 잇는 엣지(Edge)로 이루어져 있다. 그래프를 분류하는 방법에는 여러가지가 있다.
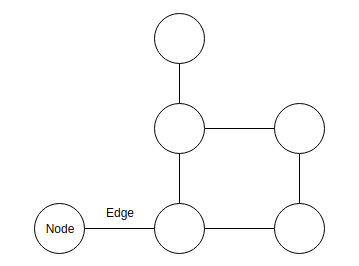
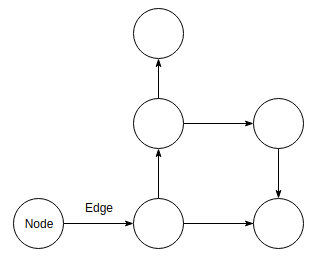
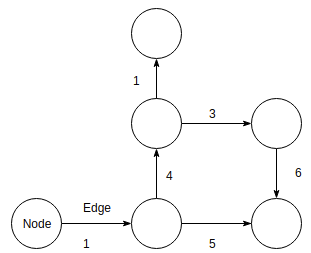
엣지의 상태에 따른 분류로는단방향 그래프(Undirected), 양방향 그래프(Directed), 가중치 그래프(Weighted)가 있다. 단방향 그래프는 말 그대로 노드 간에 방향성이 없으며 엣지(Node1, Node2)과 엣지(Node2, Node1)는 같은 의미이다. 반면 양방향 그래프는 노드간 방향성이 존재한다. 엣지(Node1, Node2)과 엣지(Node2, Node1)는 다른 의미다. 가중치 그래프는 엣지들이 값을 가지는 것이 특징이다. 가중치 그래프를 이용해 도시간 도로 연결 시 최소 비용을 구할 수 있다.
| undirected | directed | weighted |
|---|---|---|
 |  |  |
트리
노드의 상태에 따른 분류도 가능하다. 노드로 들어오는 엣지의 개수를 in-degree, 노드에서 나가는 엣지의 개수를 out-degree라고 한다. 트리(Tree) 특수한 형태의 그래프이다. 하나의 Root 노드를 가지며 in-degree가 1인 방향성을 가지는 그래프라고 할 수 있다. 트리 또한 자식노드의 위치, 노드가 가지는 데이터의 크기에 따라 분류할 수 있다.
트리는 노드로 이루어진, 계층적인 형태를 갖는 자료 구조다. 많은 양의 정보를 보기 쉽게 정리할 때 유용하며, 실생활에서 볼 수 있는 대표적인 예로는 족보, 컴퓨터 디렉토리, 회사 조직도 등이 있다.
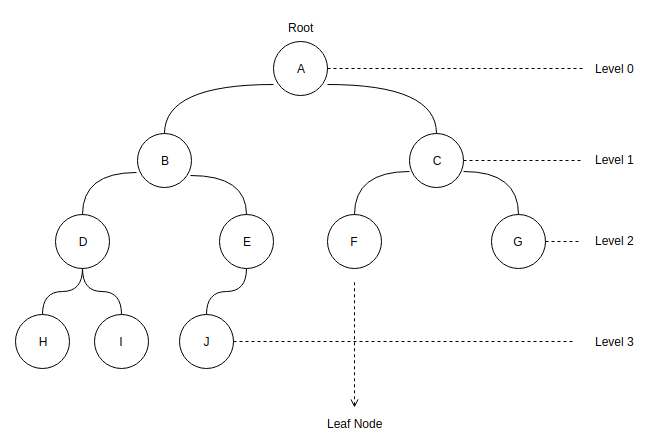
이진 트리
자식 노드를 최대 2개 가질 수 있는 노드들로만 이루어진 트리를 이진 트리(Binary Tree) 라고 하는데, 자식 노드들의 배치에 따라 완전 이진 트리, 포화 이진 트리, 정 이진 트리, 편향 이진 트리로 구분 할 수 있다. 완전 이진 트리는 왼쪽 자식 노드 부터 채워 가며, 마지막 레벨을 제외하고는 모든 자식 노드가 채워져 있는 트리이다. 포화 이진 트리는 모든 노드가 0개 혹은 2개의 자식노드를 가지며, 모든 리프 노드가 똑같은 레벨에 있는 트리이다. 정 이진 트리는 모든 노드가 0개 혹은 2개의 자식노드를 가지는 트리로, 포화 이진 트리의 하위 종류이다. 편향 이진 트리는 모든 노드들이 한 방향으로만 자식노드를 가지는 트리이다.
(이진 트리의 구분은 나중에 업데이트)
이진 탐색 트리
이진 탐색 트리(Binary Search Tree)는 이진 트리의 한 종류이다. 자식 노드를 0~2개 가지는 노드들로만 이루어져 있으며 왼쪽 자식 노드는 부모 노드보다 작고, 오른쪽 자식 노드는 부모 노드보다 크다. 데이터를 저장할 때 이미 부모 노드와 비교를 해서 저장하기 때문에 검색 속도가 빠르다.
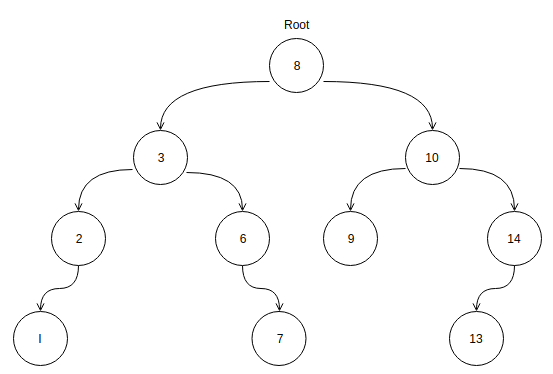
트리 순회(Tree Traversal)
| Pre-order Traversal(전위순회) | In-order Traversal(중위순회) | Post-order Traversal(후위순회) | Level-order Traversal(레벨순회) |
|---|---|---|---|
| Root 를 방문한다 => 왼쪽 subtree를 방문한다 => 오른쪽 subtree 를 방문한다 | 왼쪽 Subtree 를 방문한다 => Root 를 방문한다. => 오른쪽 | 왼쪽 subtree 를 방문한다. => 오른쪽 subtree 를 방문한다. => root 를 방문한다. | 특징 : 루트가 가장 먼저 나온다, 큐를 이용해 구현 |
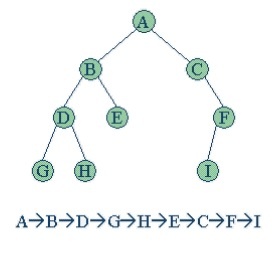 | 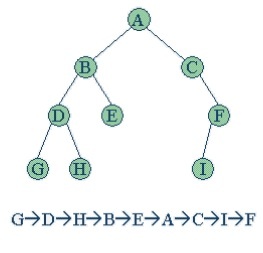 | 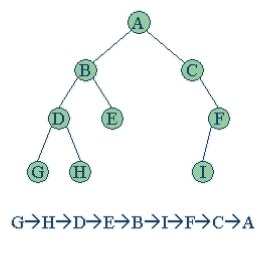 |  |
구성 및 구현 방법
그래프를 구현하는 방법은 2차원 배열을 사용하는 방법과 링크드 리스트를 사용하는 방법이 있다. 2차원 배열은 구현은 간단하지만 공간을 많이 차지하고, 링크드 리스트를 사용한 경우는 그 반대다. 그렇기 때문에 노드 개수가 적으면 2차원 배열을, 많으면 링크드 리스트를 사용하게 효율적일 수 있다.
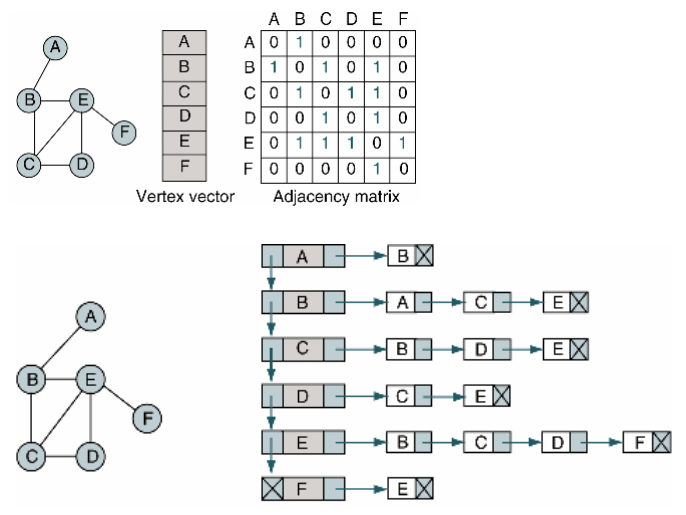
링크드 리스트를 사용하여 구현하는 방법에 대해서 정리해보자. 먼저 세가지 객체가 필요할 것이다. 노드와 엣지를 삽입하고 제거하는 메소드와 노드, 엣지 리스트를 가지고 있는 Graph 객체, 자식,부모 노드 리스트와 데이터를 가지고 있는 Node 객체, 데이터를 가지고 있는 Edge 객체.
기본적으로 그래
Object: Graph, Node, Edge
insertNode(), deleteNode()
insertEdge(), deleteEdge()
