백준 - 1002 (Python) - 터렛

백준 1002

터렛

문제

이 문제는 두 개의 터렛 각각에서 상대편 마린(타깃)까지의 거리가 주어졌을 때, 타깃이 위치할 수 있는 경우의 수를 출력하는 문제이다. 두 원의 위치 관계를 이용해서 풀이하면 된다.
각 터렛에서 타깃까지의 거리를 토대로 타깃이 위치할 수 있는 점을 조합하면 각 터렛을 중심으로 두 개의 원을 그릴 수가 있기 때문이다. 두 원의 위치 관계를 이용하기 위해선 두 터렛의 거리가 필요하다. 두 터렛의 거리를 반지름으로 하는 원이 있다고 가정하고서 원의 방정식을 활용해서 두 터렛의 거리를 구한다.

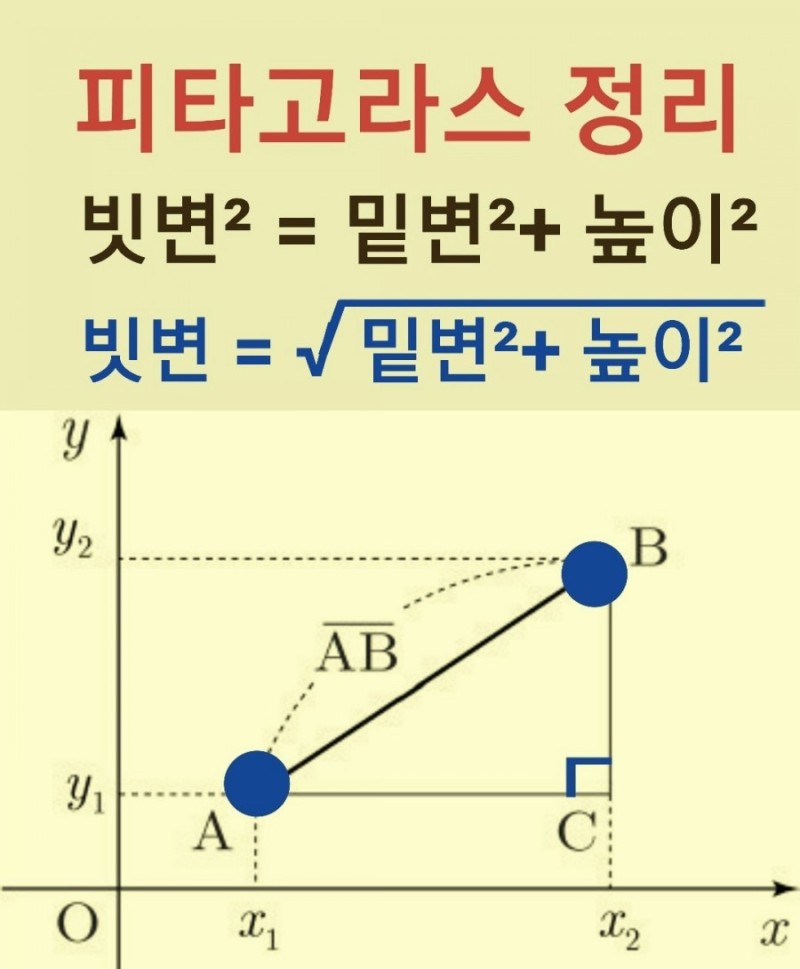
 r = ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
 #두 점의 좌표가 주어졌을 때 거리를 구하는 공식

아래 그림 설명을 보며 참고해보자.

이를 파이썬으로 표현하면 다음과 같다.

T = int(input())

for i in range(T):
    x1, y1, r1, x2, y2, r2 = map(int, input().split())

    r = ((x1 - x2)**2 + (y1 - y2)**2)**0.5
    R = [r1, r2, r]

    m=max(R)
    R.remove(m)

    if r == 0 and r1 == r2:
        print(-1)
    elif r == r1 + r2 or m == sum(R):
        print(1)
    elif m > sum(R):
        print(0)
    else:
        print(2)