[이코테] 구현

구현 문제

• 풀이를 떠올리는 것은 쉽지만 소스코드로 옮기기 어려운 문제

예시)

• 알고리즘은 간단한데 코드가 지나칠 만큼 길어지는 문제
• 실수 연산을 다루고, 특정 소수점자리까지 출력해야하는 문제
• 문자열을 특정한 기준에 따라서 끊어 처리해야하는 문제
• 적절한 라이브러리를 찾아서 사용해야하는 문제 * 순열, 조합 등

구현 능력이 요구되는 대표적인 알고리즘 유형은 완전 탐색과 시뮬레이션이 있다.

• 완전 탐색 문제는 모든 경우의 수를 다 계산해야하기 떄문에 반복문 혹은 재귀함수를 적절히 사용하며 예외 케이스를 모두 확인해야하는 경우가 많다. 그러므로 DFS/BFS 알고리즘을 사용한다
• 시뮬레이션 문제는 문제에서 제시한 알고리즘을 한 단계씩 차례대로 직접 수행하는 문제 유형을 의미한다.

왕실의 나이트

행복 왕국의 왕실 정원은 체스판과 같은 8 × 8 좌표 평면이다. 왕실 정원의 특정한 한 칸에 나이트가 서있다.
나이트는 매우 충성스러운 신하로서 매일 무술을 연마한다.
나이트는 말을 타고 있기 때문에 이동을 할 때는 L자 형태로만 이동할 수 있으며 정원 밖으로는 나갈 수 없다.
나이트는 특정 위치에서 다음과 같은 2가지 경우로 이동할 수 있다.

수평으로 두 칸 이동한 뒤에 수직으로 한 칸 이동하기
수직으로 두 칸 이동한 뒤에 수평으로 한 칸 이동하기

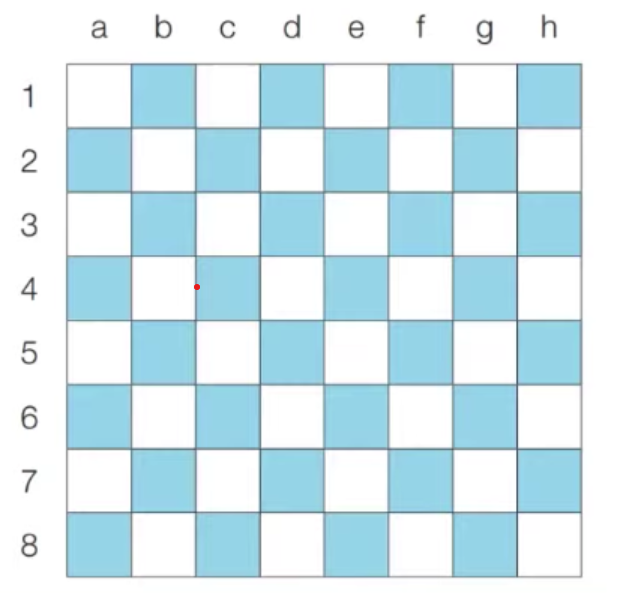
이처럼 8 × 8 좌표 평면상에서 나이트의 위치가 주어졌을 때 나이트가 이동할 수 있는 경우의 수를 출력하는 프로그램을 작성하라. 왕실의 정원에서 행 위치를 표현할 때는 1부터 8로 표현하며, 열 위치를 표현할 때는 a 부터 h로 표현한다.

c2에 있을 때 이동할 수 있는 경우의 수는 6가지이다.
a1에 있을 때 이동할 수 있는 경우의 수는 2가지이다.

입력
첫째 줄에 8x8 좌표 평면상에서 현재 나이트가 위치한 곳의 좌표를 나타내는 두 문자로 구성된 문자열이 입력된다. 입력 문자는 a1 처럼 열과 행으로 이뤄진다.

출력
첫째 줄에 나이트가 이동할 수 있는 경우의 수를 출력하시오.

해결 아이디어
나이트의 8가지 경로를 하나씩 확인하며 이동가능한지 확인한다.

• 리스트를 이용하여 8가지 방향에 대한 방향벡터를 정의한다.

# 현재 나이트의 위치 입력받기
input_data = input()
row = int(input_data[1])
column = int(ord(input_data[0])) - int(ord('a')) + 1 #ord : 유니코드 정수 반환

# 나이트가 이동할 수 있는 8가지 방향 정의
steps = [(-2, -1), (-1, -2), (1, -2), (2, -1), (2, 1), (1, 2), (-1, 2), (-2, 1)]

# 8가지 방향에 대하여 각 위치로 이동이 가능한지 확인
result = 0
for step in steps:
    # 이동하고자 하는 위치 확인
    next_row = row + step[0]
    next_column = column + step[1]
    # 해당 위치로 이동이 가능하다면 카운트 증가
    if next_row >= 1 and next_row <= 8 and next_column >= 1 and next_column <= 8:
        result += 1

print(result)

럭키 스트레이크

사고과정

• 리스트로 숫자를 하나씩 담는다.
• 전체 길이가 홀수가 있을 수 있으므로 전체길이의 반의 몫을 구해서 앞 뒤로 숫자 합을 구한다.
• 두 개를 비교한다.

내가 푼 풀이

a=list(input())
a= [int(i) for i in a]
sum=0
for i in range(len(a)//2):
  sum+=a[i]
sum1=0
for i in range(len(a)//2,len(a)):
  sum1+=a[i]
if sum1!=sum:
  print('READY')
else:
  print('LUCKY')

책풀이

# list comprehension 사용
n=input()
length=len(n)
summary=0
for i in range(len(n)//2):
	summary+=int(n[i])
for i in range(len(n)//2, length):
	summary-=int(n[i])

if summary==0:
  print('READY')
else:
  print('LUCKY')

문자열 재정렬

사고과정

• 알파벳과 숫자를 분리해서 리스트에 담는다.
• 알파벳은 정렬하고 숫자는 합을 더한다.
• 문자와 숫자 모두 붙여서 출력한다.

n=list(input())
chr=[]
s=0
for i in n:
  if i.isalpha():
    chr.append(i)
  else:
    s+=int(i)
chr.sort()
for i in chr:
  print(i, end='')
print(s)

문자열 압축

사고과정

• 압축단위를 늘려가면서 모두 확인
  • 글자 단위로 나누기
    • 앞단어와 비교해서 같으면 개수 추가.
    • 앞단어와 다르면 글자 그대로 두고 다음 단어 확인
• 가장 짧은 압축된 총 길이 비교

def solution(s):
    answer = len(s)
    # 1개 단위(step)부터 압축 단위를 늘려가며 확인
    for step in range(1, len(s) // 2 + 1):
        compressed = ""
        prev = s[0:step] # 앞에서부터 step만큼의 문자열 추출
        count = 1
        # 단위(step) 크기만큼 증가시키며 이전 문자열과 비교
        for j in range(step, len(s), step):
            # 이전 상태와 동일하다면 압축 횟수(count) 증가
            if prev == s[j:j + step]:
                count += 1
            # 다른 문자열이 나왔다면(더 이상 압축하지 못하는 경우라면)
            else:
                compressed += str(count) + prev if count >= 2 else prev
                prev = s[j:j + step] # 다시 상태 초기화
                count = 1
        # 남아있는 문자열에 대해서 처리
        compressed += str(count) + prev if count >= 2 else prev
        # 만들어지는 압축 문자열이 가장 짧은 것이 정답
        answer = min(answer, len(compressed))
    return answer

# 남아있는게 이해가 안감
def solution(s):
    result=[]
    
    if len(s)==1:
        return 1
    
    for step in range(1, len(s)+1):
        compressed  = ''
        count = 1
        prev=s[:step]

        for j in range(step, len(s)+step, step):
            
            if prev == s[j:j + step]:
                count += 1
            else:
                if count!=1:
                    compressed += str(count)+prev
                else:
                    compressed+=prev
                    
                prev=s[j:j+step]
                count = 1
                
        result.append(len(compressed))
        

    return min(result)

상하좌우 문제

NXN 크기의 정사각형 공간에서 (1,1)에서 시작으로 상,하,좌,우 방향으로 이동한다. 공간 밖으로 나가는 방향은 무시한다.

해결 아이디어

개체를 차례대로 이동시킨다는 점에서 시뮬레이션 유형으로 구분됨. 시뮬레이션 유형, 구현유형, 완전탐색 유형은 유사한 점이 많다.

• 행렬과 같음 . dx는 행 (세로로 이동), dy는 열(가로로 이동)

0,0	0,1	0,2
1,0	1,1	1,2
2,0	2,1	2,2

n=int(input())
x,y=1,1
plans=input().split()

dx=[0,0,-1,1]
dy=[-1,1,0,0]
move=['l','r','u','d']
# 이동계획 하나씩 확인
for plan in plans:
   # 이동후 좌표 구하기
   for i in range(len(move)):
     if plan==move[i]:
       nx=x+dx[i]
       ny=y+dy[i]
   # 공간 벗어나는 경우 무시
   if nx<1 or ny<1 or nx>n or ny>n:
     continue
   # 이동수행
   x,y=nx, ny
print(x,y)

시각

모든 시각 중 3이 하나라도 포함되는 경우의 수를 구하는 프로그램을 작성하시오

해결 아이디어

가능한 모든 시각(246060=86400)의 경우를 하나씩 세서 풀 수 있는 문제. 완전 탐색 문제 유형

n=int(input()) # 포함될 숫자 
cnt=0
for i in range(n+1): #시
  for j in range(60): #분
    for k in range(60): #초
      if '3' in str(i)+str(j)+str(k):
        cnt+=1

print(cnt)