YOLO나 DETR과 같은 Object detection 모델을 학습함에 있어 예측 bbox와 gt bbox의 차이를 줄여 더 객체에 핏한 박스를 예측하는 bbox regression은 매우 중요합니다. 이번 블로그 포스트에서는 bbox regression을 위해 사용되는 중요한 스코어이자 메트릭(metric)인 IoU의 정의에 대해서 알아보고 이를 Python으로 구현해보는 시간을 가져보도록 하겠습니다.

Intersection over Union (IoU)

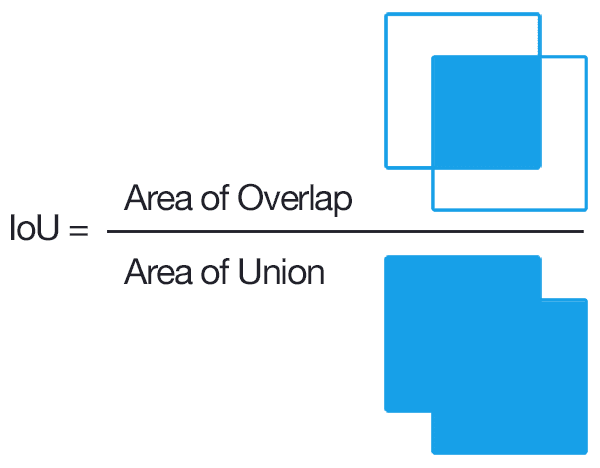
Intersection over Union 줄여서 IoU는 object detection 분야에서 객체의 bounding box 예측 값과 정답 사이의 오차를 0에서 1 사이의 값으로 나타낸 지표라고 할 수 있습니다. 여기서 0은 두 박스가 겹치지 않는다는 것을 의미하고 1은 완벽하게 겹침을 의미합니다. 이를 수식으로 표현하면 다음과 같습니다.

$IoU = \frac{|A \cap B|}{|A \cup B|}$
수식을 풀어서 설명하자면 bounding box A와 B의 IoU 값은 아래의 그림과 같이 두 박스가 겹치는 넓이 값을 두 박스의 합집합의 넓이로 나눈 값이라고 할 수 있습니다. 이를 미뤄보아 두 박스가 겹치지 않으면 그 넓이는 0이므로 IoU 값이 0이 되고, 두 박스가 완전히 겹친다면 두 박스의 합집합은 곧 교집합과 같으므로 IoU 값이 1이 됨을 알 수 있습니다.

Retrieved From https://www.google.com/url?sa=i&url=https%3A%2F%2Fpyimagesearch.com%2F2016%2F11%2F07%2Fintersection-over-union-iou-for-object-detection%2F&psig=AOvVaw2DiwRU2zNSSFiNKt1FZMYV&ust=1723471194652000&source=images&cd=vfe&opi=89978449&ved=0CBQQjhxqFwoTCJDCntSM7YcDFQAAAAAdAAAAABAE

Implementation

IoU 값을 정의하였으니 이제 이를 파이썬 코드로 구현해보도록 하겠습니다. 이를 곧장 구현하기에 먼저 bounding box (줄여서 Bbox라고 칭하겠습니다.) 클래스부터 정의해보겠습니다. 2차원에서 정의된 Bbox는 보통 두 가지 방법으로 표현할 수 있는데 이는 top left 좌표와 bottom right 좌표 값으로 표현하는 것과 박스의 중심 좌표와 너비 그리고 높이로 표현하는 방식이 있습니다. 그 중에서 이 포스트에서는 전자를 사용하도록 하겠습니다.

class Bbox:
	def __init__(self, x1, y1, x2, y2):
    	assert x2 > x1 and y2 > x1
    	self.top_left = (x1, y1)
        self.bottom_right = (x2, y2)
    def area(self):
    	width = self.bottom_right[0] - self.top_left[0]
        height = self.bottom_right[1] - self.top_left[1]

여기서 bottom_right 좌표 값은 top_left의 것보다 크다는 것이 일반적이기에 assert문을 걸어줬습니다.

그 다음으로는 해당 bbox의 넓이를 구하는 메소드를 추가했는데요. 여기서 의문이 들 수 있는 부분이 y좌표를 하단의 것에서 상단의 것을 빼는 것일 수 있습니다. 이미지의 좌표 값을 정의할 때 x좌표는 좌측에서 우측으로 갈수록, y좌표는 상단에서 하단으로 내려갈수록 값이 커진다는 것을 인지하시면 자연스럽게 이해가 가시리라 생각합니다.

이제 이 클래스에 다른 bbox 객체를 인자로 받아서 IoU의 분자 값인 intersection의 넓이을 구하는 메소드를 추가하고, $A\cup B=A+B-A\cap B$ 정의를 기반으로 두 bbox의 너비를 더하고 이 값에서 intersection 값을 빼주어 합집합의 넓이를 구하면 목표에 금방 다다를 것입니다!

    def intersection(self, other):
        x1 = max(self.top_left[0], other.top_left[0])
        y1 = max(self.top_left[1], other.top_left[1])
        x2 = min(self.bottom_right[0], other.bottom_right[0])
        y2 = min(self.bottom_right[1], other.bottom_right[1])
        
        if x2 <= x1 or y2 <= y1:
            return 0
        
        return (x2 - x1) * (y2 - y1)

이 메소드를 쉽게 이해하기 위해 위 그림을 다시 참고해보면 intersection 부분을 새로운 박스라고 생각해볼게요. 이 박스의 top_left 좌표는 두 박스의 top_left 좌표 중 더 큰 값을 가지는 점이 될 것이고, bottom_right의 것은 반대로 더 작은 값이 될 것입니다. 따라서 x1, x2, y1, y2를 위 코드와 같이 정의해주면 되고 만약 x2,y2 중 둘 중 하나라도 각각 x1, y1보다 작다면 그것은 두 박스가 겹치지 않는다는 것을 의미하므로 intersection 값은 0이고 이를 반환해주면 됩니다. 반면, 이 if문에 걸리지 않는 경우라면 width (x2-x1) 와 height(y2 - y1)을 곱하여 반환하면 됩니다.

이제 다왔습니다. 대망의 iou 메소드를 구현해보도록 하겠습니다. 구현은 간단합니다. 위 intersection 메소드를 활용해 두 박스의 겹치는 영역의 넓이를 구하고 이를 두 박스의 넓이의 합에서 빼주면서 합집합 영역으로 정의하고 이 둘의 비율을 반환해주면 됩니다.

    def iou(self, other):
        intersection_area = self.intersection(other)
        union_area = self.area() + other.area() - intersection_area
        
        if union_area == 0:
            return 0
        
        return intersection_area / union_area

지금까지 object detection 태스크에서 중요한 IoU의 정의와 python 구현에 대해서 알아봤습니다. 이 글을 읽고 나면 생길 수 있는 질문이 "그래서 이 값을 어떻게 쓰는거죠?" 일 수 있는데, 실제로 object detection 모델을 학습함에 있어서 이 IoU 값은 다양한 방식으로 활용됩니다.

예를 들어, IoU 값에 threshold를 정해서 모델이 예측한 bbox와 gt bbox가 비교할만한 대상인지를 판단할 수 있습니다. 우리는 이를 일반적으로 background / foreground prediction이라고 구분하기도 합니다. 또한, 그 유명한 NMS(Non-Maximum Suppression) 알고리즘에서도 IoU 값이 중요하게 사용되어 중복 검출을 제거하는 데 활용됩니다.

하지만 IoU의 활용은 여기서 그치지 않습니다. IoU는 단순히 평가 지표나 후처리 과정에서만 사용되는 것이 아니라, 모델의 학습 과정에서도 중요한 역할을 합니다. 이는 IoU를 기반으로 한 loss 함수들이 개발되어 있기 때문입니다.

따라서 다음 포스트에서는 이러한 IoU의 심화 활용에 대해 더 자세히 알아보겠습니다. 구체적으로, IoU 값을 training의 loss로서 활용하는 방법과 좀 더 일반화된 IoU의 변형 예제들을 살펴보겠습니다. 이를 통해 IoU가 object detection 분야에서 얼마나 폭넓게 사용되고 있는지, 그리고 어떻게 발전해왔는지를 이해할 수 있길 기대합니다.

읽어주셔서 감사드리고 언제나 피드백 및 댓글은 환영입니다~~ㅎㅎ