Graph
자료구조에서의 그래프는 여러개의 점들이 선으로 이어져 있는 복잡한 네트워크 망의 모습을 띄고 있음.
그래프에서의 점: 정점(vertex) , 선 : 간선 (edge)
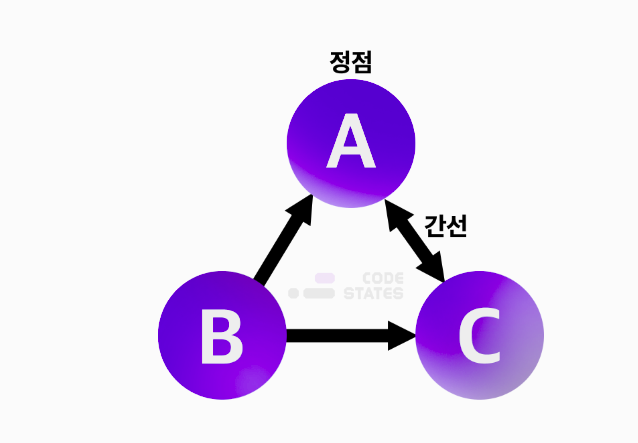
그래프용어
- 무(방)향 그래프 (undirected graph) : 정점과 정점이 서로 쌍방향으로 이어져 있는것.
반대는 단방향(directed)이며, 한쪽에서만 접근이 가능하고 나머지 하나에서는 접근이 불가.(일방통행) - 진입차수(in-degree)/ 진출차수(out-degree): 한 정점에 진입하고 진출하는 간선이 몇개인지 나타냄.
- 인접(adjacency): 두 정점간에 간선이 직접 이어져 있다면 두 정점은 인접한 정점
- 자기 루프(self loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 특징으로는 다른 정점을 거치지 않는다는것이 특징
- 사이클(cycle) : 한 정점에서 출발하여 다시 해당 정점으로 돌아간다면 사이클이 있다고함.
인접행렬
그래프 용어에서도 나온 인접을 이용한 행렬이며 서로 다른 정점들이 인접한 상태인지를 표시한 행렬으로 22차원 배열의 형태로 나타냄.
예시(위의 그래프와 동일함)
let a = [
[0,0,1], //A라는 정점이 C라는 정점을 바라본다는 의미
[1,0,1], //B라는 정점은 A와 C를 바라본다는 의믜
[1,0,0] //C라는 정점이 A라는 정점을 바라본다는 의믜
]인접 행렬은 두 정점 사이에 관계가 있는지 없는지를 확인하려고 사용하며 가장 빨느 경로를 찾고자 할 때 주로 사용.
Tree
자료구조의 트리는 나무를 뒤집어 놓은듯한 모습을 가지고 있음. 그래프의 여러 구조중 무방향 그래프의 한 요소이며 하나의 뿌리로부터 가지가 사방으로 뻗은 형태
트리구조는 데이터가 바로 아래에 있는 하나 이상의 데이터에 무방향으로 연결된 계층적 자료구조
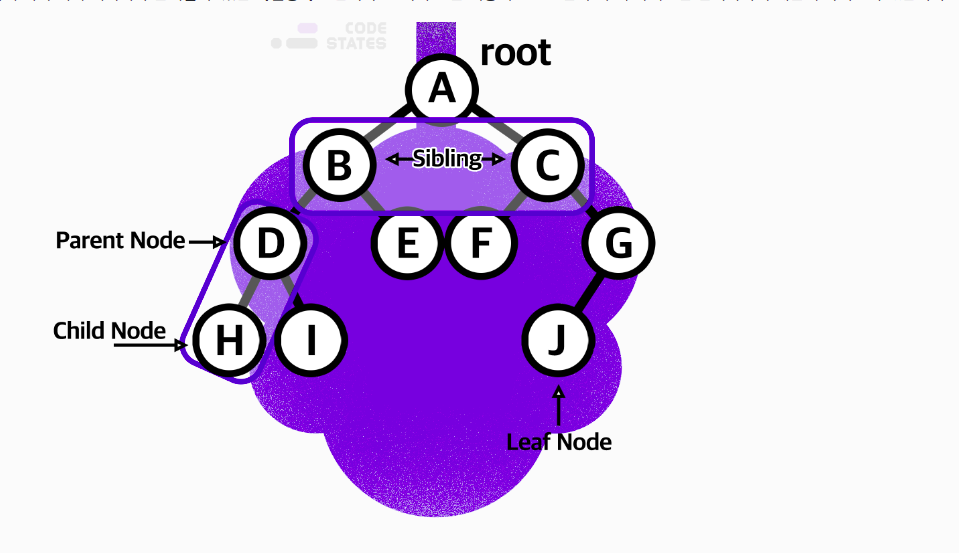
Tree용어 정리
- 노드(Node) : 트리 구조를 이루는 모든 개별 데이터
- 루트(Root) : 트리 구조의 시작점이 되는 노드
- 부모 노드(Parent node): 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
- 자식 노드(Cild node)두 노드가 상하 관계로 연결되어 있을때 상대적으로 루트에서 먼 노드
- 리프(Leaf) : 트리구조의 끝 지점이고 자식 노드가 없는 노드
Tree의 깊이, 높이 ,레벨
-
깊이 (depth) : 트리구조에서 루트로부터 하위 계층의 특정 노드까지의 깊이(depth)를 의미함.
루트 노드의 depth는 0이며(디폴트), 하나씩 아래로 내려올때마다 depth가 1씩 늘어남. -
레벨 (Level) : 트리구조에서 같은 깊이를 가지고 있는 노드를 묶어서 레벨로 표현 depth가 0인 루트의 레벨은 1이며 depth가 1씩 늘어날수록 level또한 1씩 늘어남.(디폴트 레벨은 root인 1)별도로 같은 레벨에 나란히 서있는 노드를 형제 노드(sibling Node)라고 함.
-높이 (Height) 트리 구조에서 리프 노드를 기준으로 루트까지의 높이(height)를 나타냄,최초 디폴트 값은 0
-서브트리 (Sub tree) 트리구조에서 root로 뻗어나오는 큰 트리의 내부에 또 다시 트리 구조를 갖춘 작은 트리를 서브 트리라고 함.
Tree의 탐색
트리 구조는 편리한 구조를 전시하는 것 외에 효율적인 탐색을 위해서도 사용함.
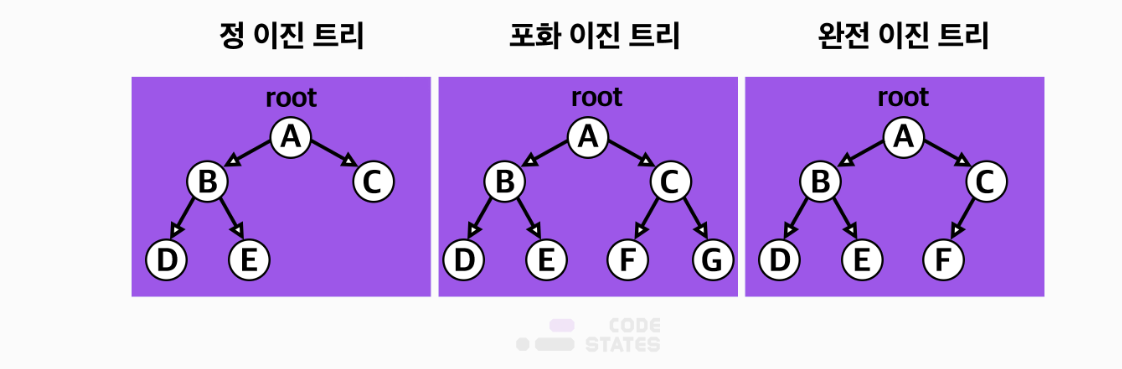
대표적인 트리구조는 이진 트리(binary tree)와 이진 탐색 트리(binary search tree)가 있음.
이진트리(Binary tree)
자식 노드가 최대 두 개인 노드들로 구성된 트리
두 개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나눌 수 있음.
이진트리는 자료 삽입, 삭제 방법에 따라 세가지 트리로 나뉨

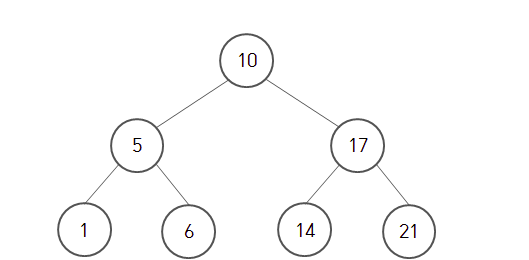
이진 탐색 트리(Binary Search Tree)
모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있음.
이진 탐색 트리는 균형 잡힌 트리가 아닐 경우, 입력되는 값의 순서에 따라 한쪽으로 노드들이 몰리게 될 수 있음(전부다 루트보다 큰값이면 오른쪽으로 쏠려버리기 때문)
사진으로 이해하면 더 빠르다.