Kruskal MST(Minimum Spanning Tree)을 활용한, 최소 비용 간선 구하기(Union & Find 이용) in C++

각 정점을 연결하는 간선의 최소 연결합을 출력하는 코드

정점의 수 v, 모든 간선의 수 e,
e개의 간선에 대해서는 출발 정점, 도착 정점, 간선의 비용이 주어진다.

#include <iostream>
#include <vector>
using namespace std;

struct Data {
    int s, e, val;
    Data(int a, int b, int c) {
        s = a;
        e = b;
        val = c;
    }
    bool operator< (const Data &d) const {
        return val<d.val;
    }
};
int v, e, res;
int unf[1001];
vector<Data> V;

int Find(int v) {
    if (v == unf[v]) return v;
    else return unf[v] = Find(unf[v]);
}
int Union(int a, int b) {
    int fa = Find(a);
    int fb = Find(b);
    if (fa != fb) unf[fa] = fb;
}

int main() {
    freopen("input.txt", "rt", stdin);
    cin >> v >> e;
    for(int i=1; i<=v; i++) {
        unf[i] = i;
    }
    for(int i=1; i<=e; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        V.push_back(Data(a, b, c));
    }
    sort(V.begin(), V.end());		// 오름 차순 정렬
    for (int i = 0; i < e; i++) {
        int fa = Find(V[i].s);
        int fb = Find(V[i].e);
        if (fa != fb) {		// 연결된 간선이 아니라면 res에 덧셈
            res += V[i].val;
            Union(V[i].s, V[i].e);
        }
    }
    cout << res;
    return 0;
}

간선의 비용에 따라 간선을 오름차순으로 정렬한뒤, 각 간선들을 연결해 나간다.

• struct Data : 출발 정점, 도착 정점, 간선의 비용을 저장하기위한 구조체
• bool operator < (const Data &d) const : Data 구조체에 sort함수 사용시 정렬의 기준을 정하기 위한 것이다.
• unf[1001] : Union & Find를 사용하기 위한 배열
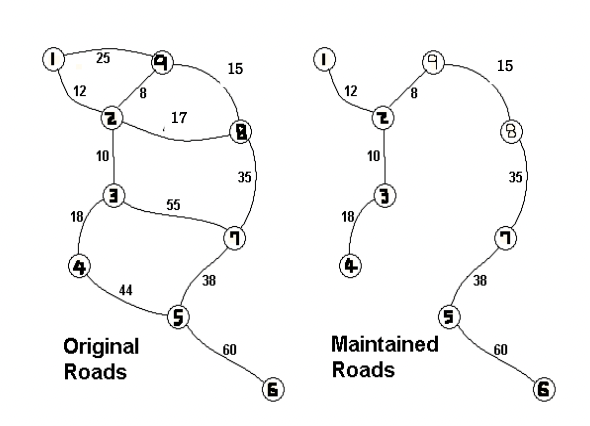
  ex)
  9 12
  1 2 12
  1 9 25
  2 3 10
  2 8 17
  2 9 8
  3 4 18
  3 7 55
  4 5 44
  5 6 60
  5 7 38
  7 8 35
  8 9 15