- 이것이 취업을 위한 코딩테스다 with 파이썬(이코테 2021) 유튜브 영상을 보면서 공부한 자료입니다.
- https://www.youtube.com/watch?v=m-9pAwq1o3w&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC
그리디 알고리즘
- 탐욕법이라고도 한다.
- 지금 당장 좋은 것을 선택하는 방법론을 의미한다.
- 일반적인 상황에서, 그리디 알고리즘은 최적의 해를 보장할 수 없을 때가 많다.
- 따라서 주어진 문제 상황에서, 그리디 알고리즘이 최적의 해를 보장하는지 생각해 보아야 한다.
<문제 1> 거스름 돈

입력 예시
1260
500 100 50 10
- 1번째 입력은 N
- 2번째 입력은 사용 가능 거스름돈
출력 예시
6
<풀이 1> 거스름 돈
문제 해결 아이디어
- 가장 큰 화폐 단위부터 돈을 거슬러 주면된다.
- 500원, 100원, 50원, 10원 동전을 차례대로 거슬러 준다.
정당성 분석
- 위 문제의 경우, 큰 단위의 동전이, 항상 작은 단위의 동전의 배수이기 때문에 탐욕법이 해답이 된다.
- 만약 500원, 400원, 100원의 동전이 주어진다면, 이 경우에는 탐욕법은 해답이 될 수 없다.
n = int(input())
coins = list(map(int, input().split()))
res = 0
for coin in coins:
res += n // coin
n = n % coin
print(res)
시간 복잡도
- 화폐의 종류만큼 for loop가 실행된다.
- 화폐의 종류가 k라고 할 때, 시간 복잡도는 O(k)이다.
<문제 2> 1이 될 때가지

입력 예시
25 5
- 첫째 줄에 N과 K가 공백을 기준으로 하여 각각 자연수로 주어진다.
출력 예시
2
- 첫째 줄에 N이 1이 될 때까지, 1번 혹은 2번의 과정을 수행해야 하는 횟수의 최솟값을 출력한다.
<풀이 2> 1이 될 때까지
문제 해결 아이디어
- 최대한 많이 나누기 연산을 해야 한다.
- 단, K가 2 이상이어야 한다.
n, k = map(int, input().split())
res = 0
while True:
target = (n // k) * k
res = res + (n - target)
n = target
if n < k:
break
res += 1
n = n // k
res = res + (n - 1)
print(res)<문제 3> 곱하기 혹은 더하기

입력 예시 1
02984
출력 예시 1
576
입력 예시 2
567
출력 예시 2
210
<풀이 3> 곱하기 혹은 더하기
문제 해결 아이디어
- 곱셈 연산이 더 큰 값을 만든다.
- 다만 두 수 중에 하나라도 0 혹은 1인 경우, 더하기를 수행하는것이 더 큰 값을 만든다.
- 즉, 두 수중에 하나라도 1이하라면, 더하기를 수행하는 것이 더 큰 값을 만든다.
data = list(map(int, input()))
res = data[0]
for i in range(1, len(data)):
if res <= 1 or data[i] <= 1:
res += data[i]
else:
res *= data[i]
print(res)<문제 4> 모험가 길드

입력 예시
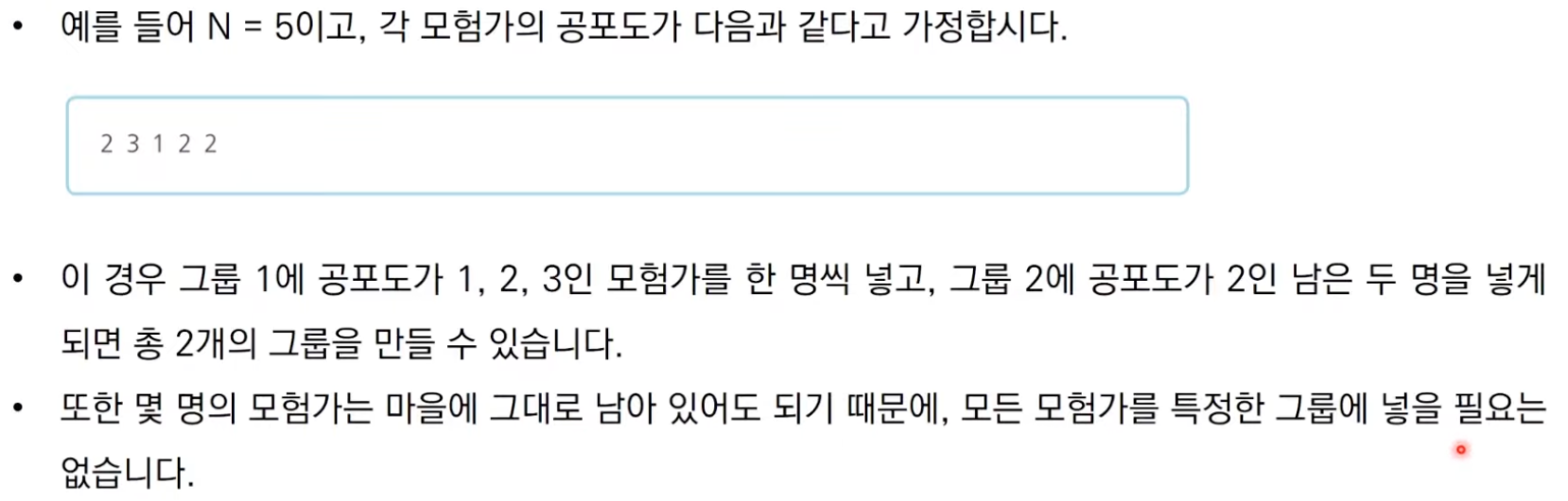
5
2 3 1 2 2
- 첫째 줄제 모험가의 수 N이 주어진다.
- 둘째 줄에 각 모험가의 공포도의 값을 N 이하의 자연수로 주어지며, 각 자연수는 공백으로 구분한다.
출력 예시
2
- 여행을 떠날 수 있는 그룹 수의 최댓값을 출력한다.
<풀이 4> 모험가 길드
문제 해결 아이디어
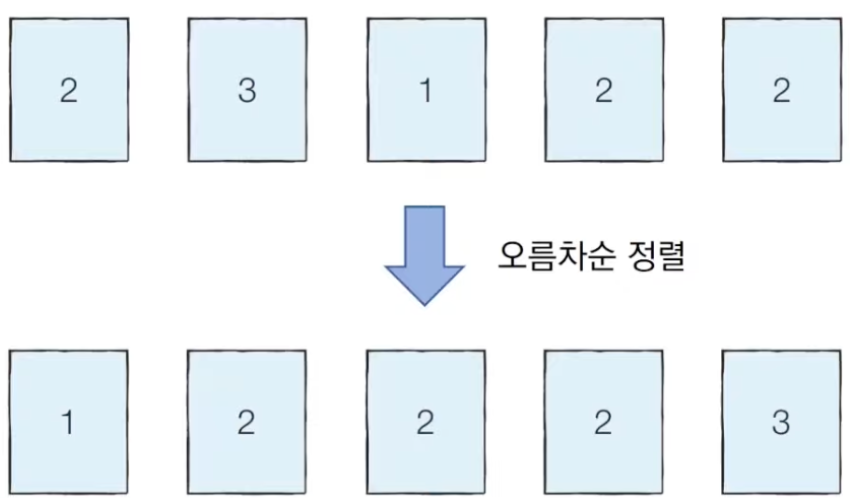
- 오름차순 정렬 이후에, 공포도가 가장 낮은 모험가부터 하나씩 확인한다.
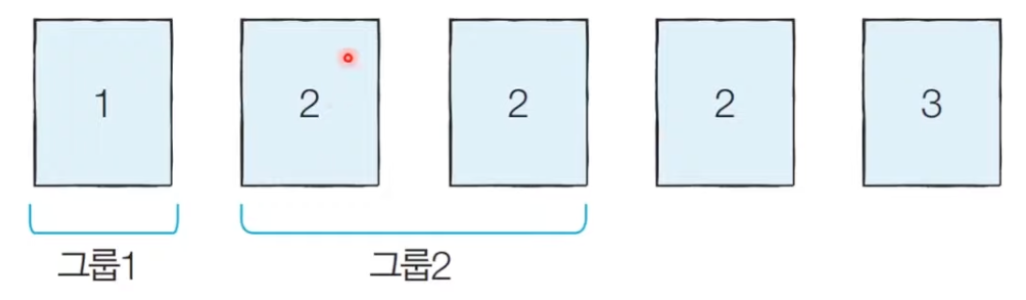
- '현재 그룹에 포함된 모험가의 수' >= '현재 확인하고 있는 공포도'라면, 이를 그룹으로 설정한다.
n = int(input())
data = list(map(int, input().split()))
data.sort()
res = 0
cnt = 0
for d in data:
cnt += 1
if cnt >= d:
res += 1
cnt = 0
print(res)
