- 이것이 취업을 위한 코딩테스다 with 파이썬(이코테 2021) 유튜브 영상을 보면서 공부한 자료입니다.
- https://www.youtube.com/watch?v=m-9pAwq1o3w&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC
서로소 집합
- 서로소 집함(Disjoint Sets)란 공통 원소가 없는 두 집합을 의미한다.
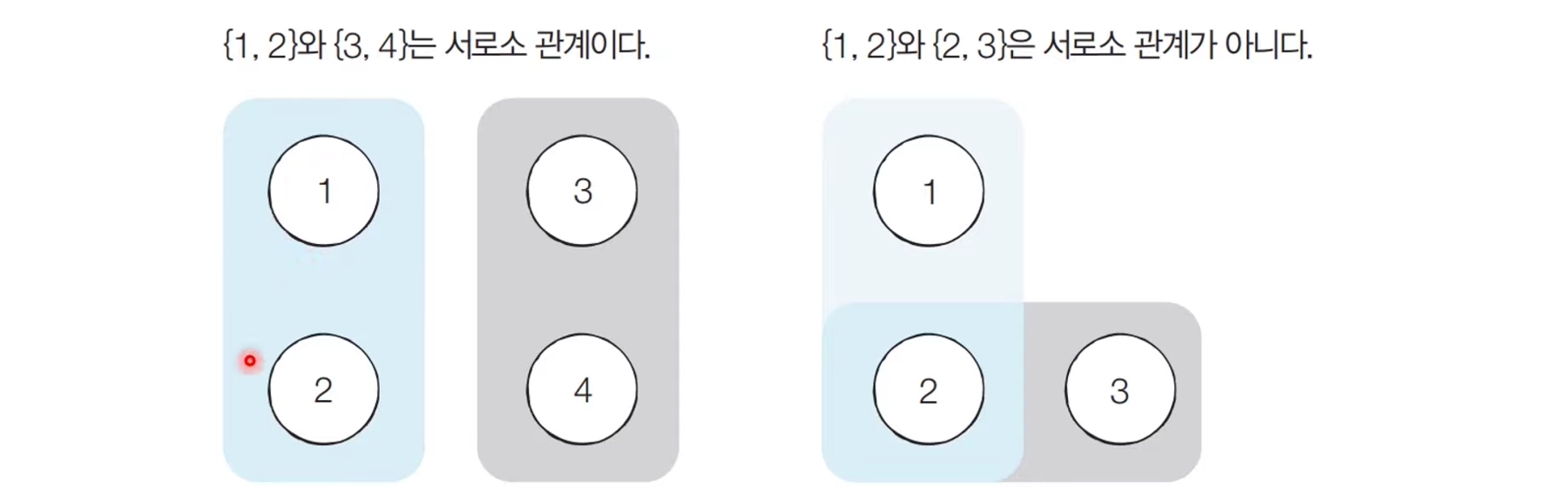
서로소 집합 자료구조
- 서로소 부분 집합들로 나뉘어진 원소들의 데이터를 처리하기 위한 자료구조이다.
- 서로소 집합 자료구조는 두 종류의 연산을 지원한다.
- 합집합(Union): 두 개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산이다.
- 찾기(Find): 특정한 원소가 속한 집합이 어떤 집합인지 알려주는 연산이다. - 서로소 집합 자료구조는 합치기 찾기(Union Find) 자료구조라고 불리기도 한다.

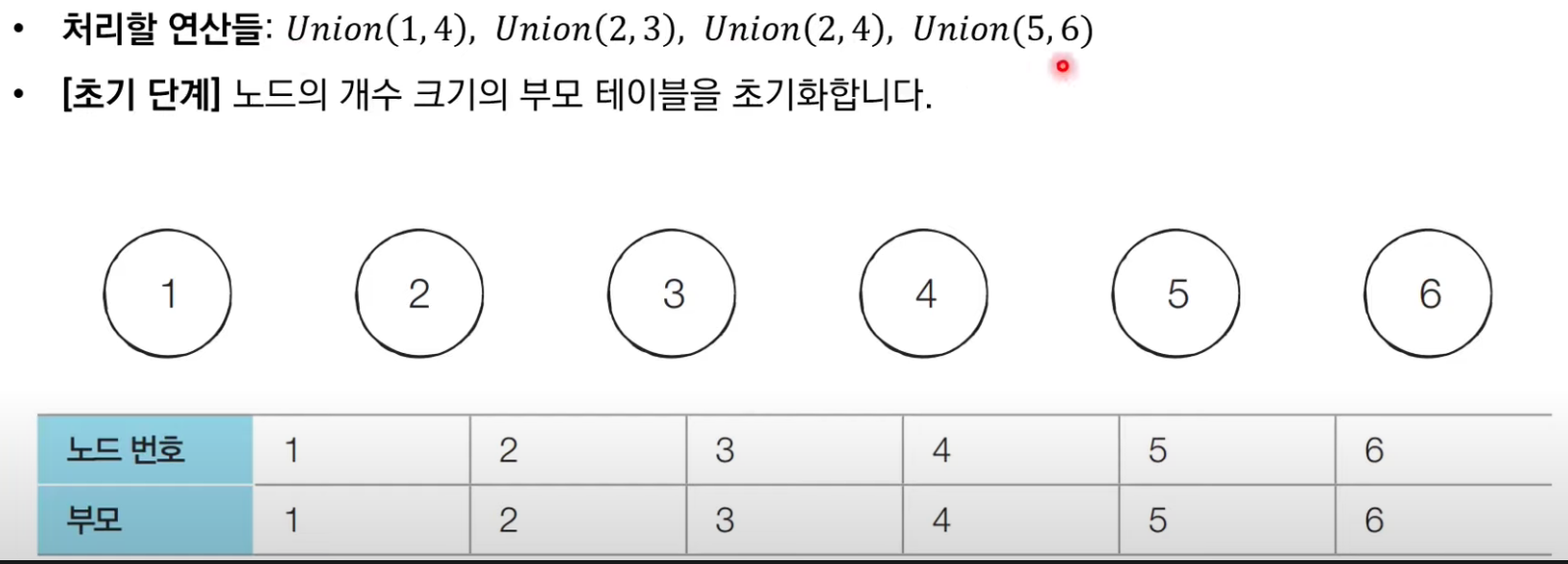
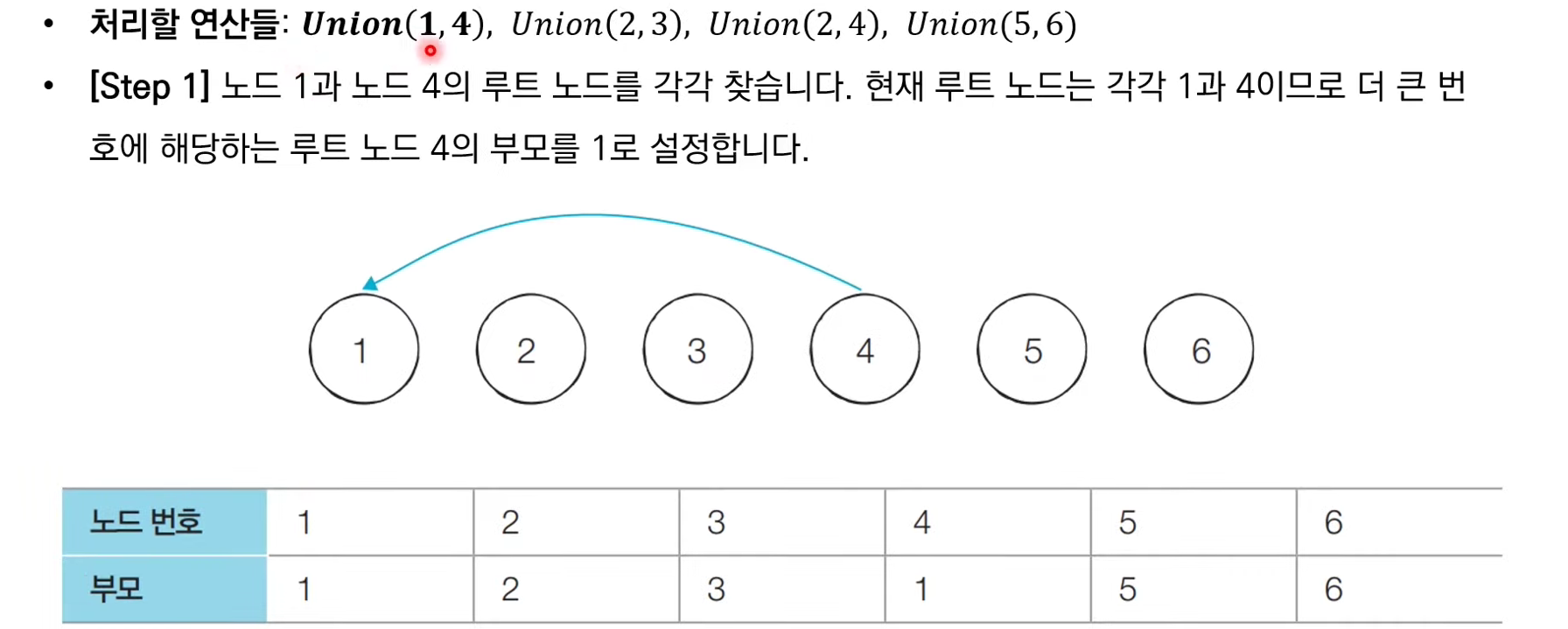
서로소 집합 자료구조: 동작 과정 살펴보기
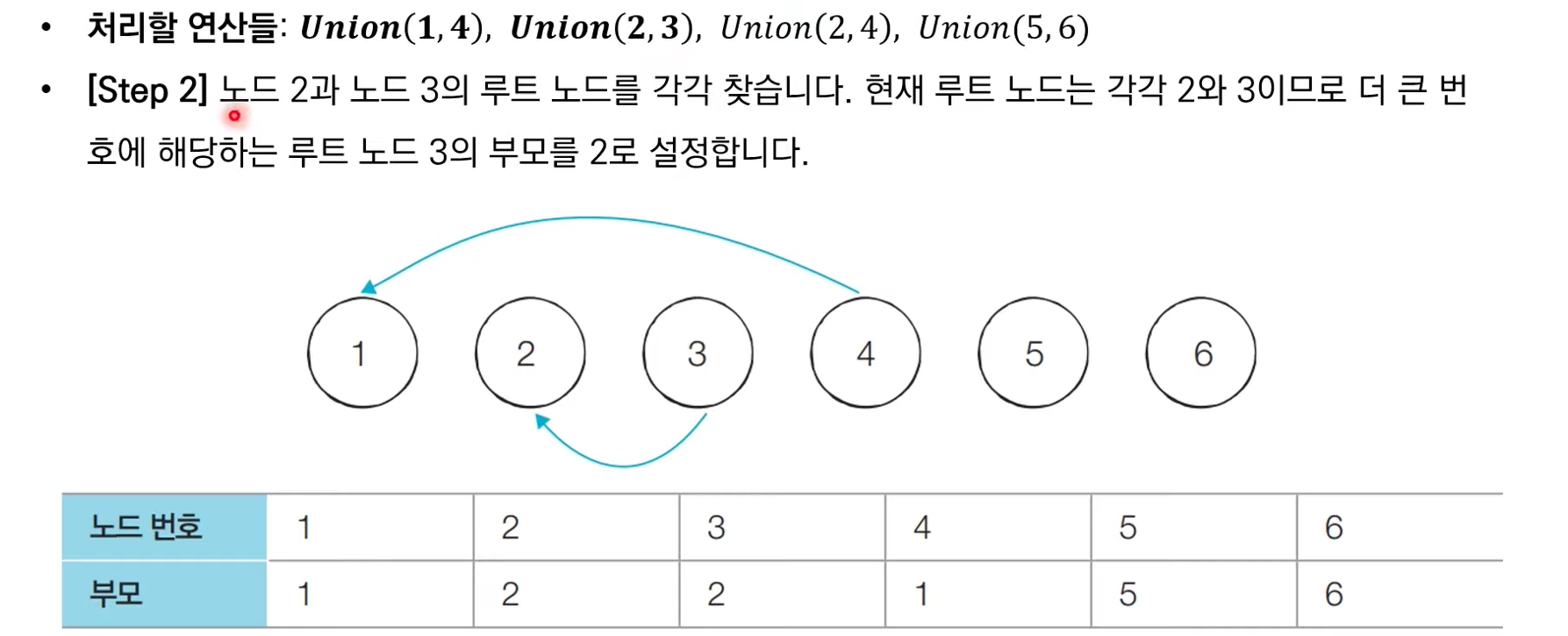
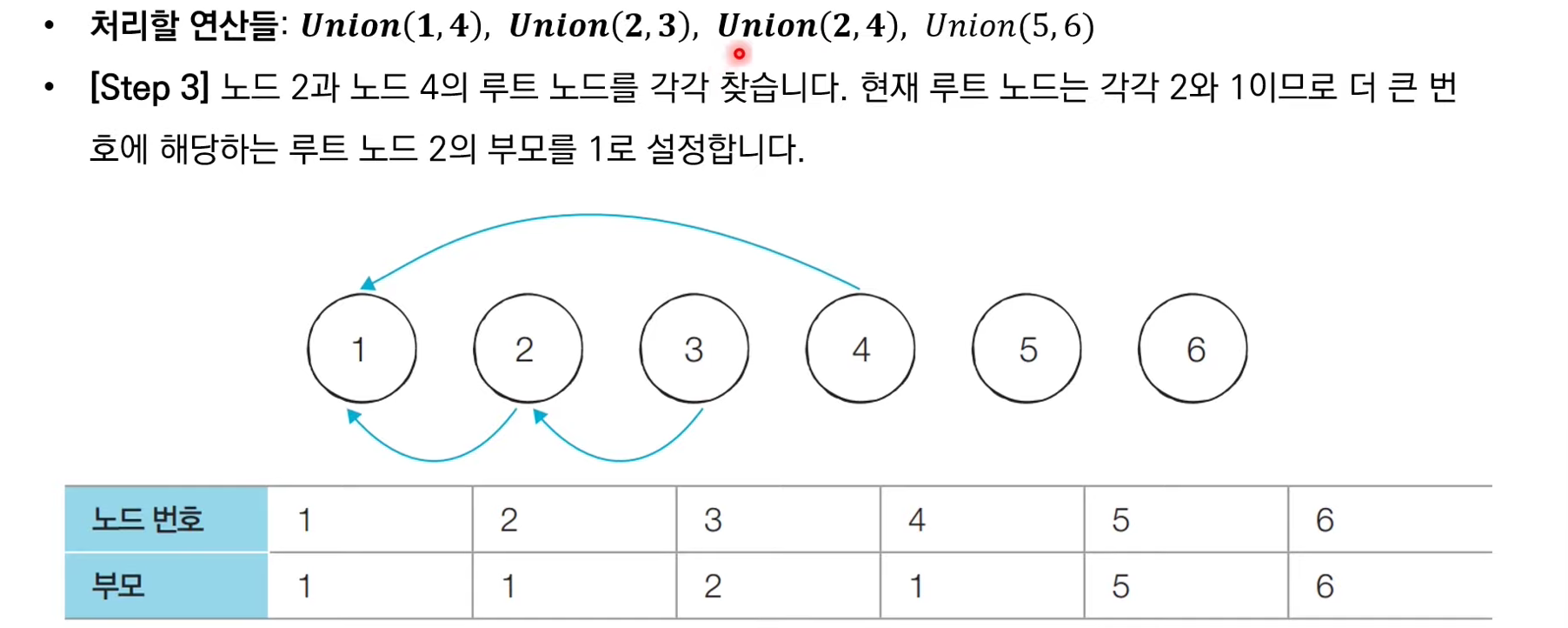
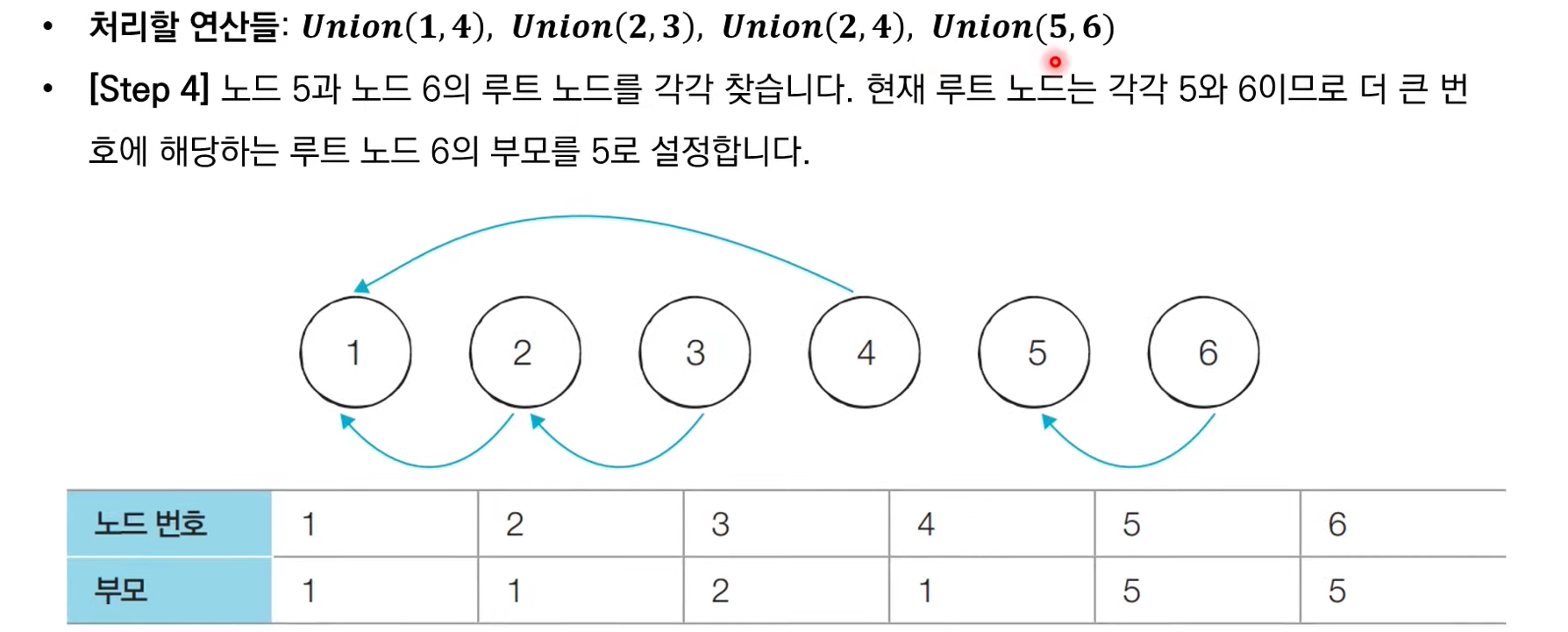
서로소 집합 자료구조: 경로 압축
- 찾기(Find) 함수를 최적화하기 위한 방법으로, 경로 압축(Path Compression)을 이용할 수 있다.
- 찾기(Find) 함수를 재귀적으로 호출한 뒤에, 부모 테이블 값을 바로 갱신한다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 떄까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
- 서로소 집합 자료구조: 경로 압축 적용
입력 예시
6 4
1 4
2 3
2 4
5 6
- 첫번째 줄에 vertex 수, 입력 예시 수 e가 입력된다.
- 두번째 줄부터 e+1번째 줄까지, 입력 예시가 입력된다.
출력 예시
1 1 1 1 5 5
- 각 vertex가 속한 집합을 나타내는 최상단 root 원소를 출력한다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드를 찾을 때까지 재귀 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(Union 연산)의 개수 입력 받기
v, e = map(int, input().split())
# 부모 테이블 초기화하기
parent = [0] * (v + 1)
# 부모 테이블에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
# Union 연산을 각각 수행
for i in range(e):
a, b = map(int, input().split())
union_parent(parent, a, b)
# 각 원소가 속한 집합 출력하기
print('각 원소가 속한 집합: ', end='')
for i in range(1, v + 1):
print(find_parent(parent, i), end=' ')
print()
# 부모 테이블 내용 출력하기
print('부모 테이블: ', end='')
for i in range(1, v + 1):
print(parent[i], end=' ')서로소 집합을 활용한 사이클 판별
- 서로소 집합은 무방향 그래프 내에서의 사이클 판별을 할때 사용할 수 있다.
- 방향 그래프 내에서의 사이클 판별은, DFS를 이용하여 판별할 수 있다.
- 사이클 판별 알고리즘은 다음과 같다.

입력 예시
6 4
1 4
2 3
2 4
5 6
- 첫번째 줄에 vertex 수, 입력 예시 수 e가 입력된다.
- 두번째 줄부터 e+1번째 줄까지, 입력 예시가 입력된다.
출력 예시
사이클이 발생하지 않았습니다.
- 사이클이 발생했다면, "사이클이 발생했습니다."를 출력한다.
- 사이클이 발생하지 않았다면, "사이클이 발생하지 않았습니다."를 출력한다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드를 찾을 때까지 재귀 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(Union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1)
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
# 사이클 발생 여부
cycle = False
for i in range(e):
a, b = map(int, input().split())
# 사이클이 발생한 경우 종료
if find_parent(parent, a) == find_parent(parent, b):
cycle = True
break
# 사이클이 발생하지 않았다면 합집합(Union) 연산 수행
else:
union_parent(parent, a, b)
if cycle:
print("사이클이 발생했습니다.")
else:
print("사이클이 발생하지 않았습니다.")신장 트리
- 그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다.
- 모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건은 트리의 조건이기도 하다.
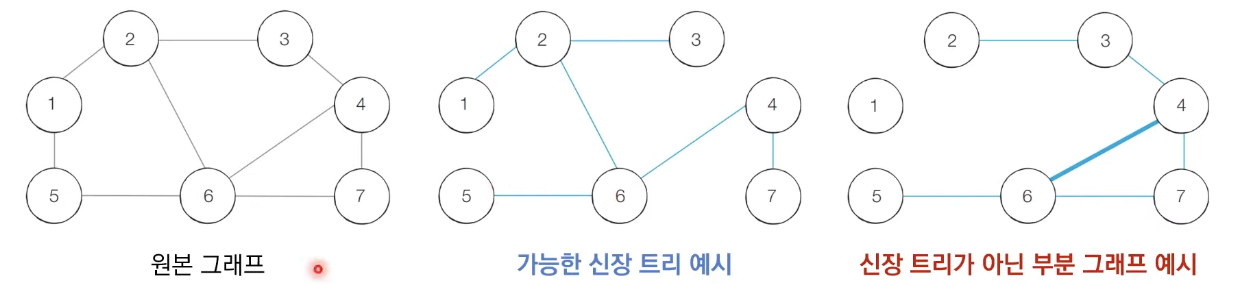
최소 신장 트리
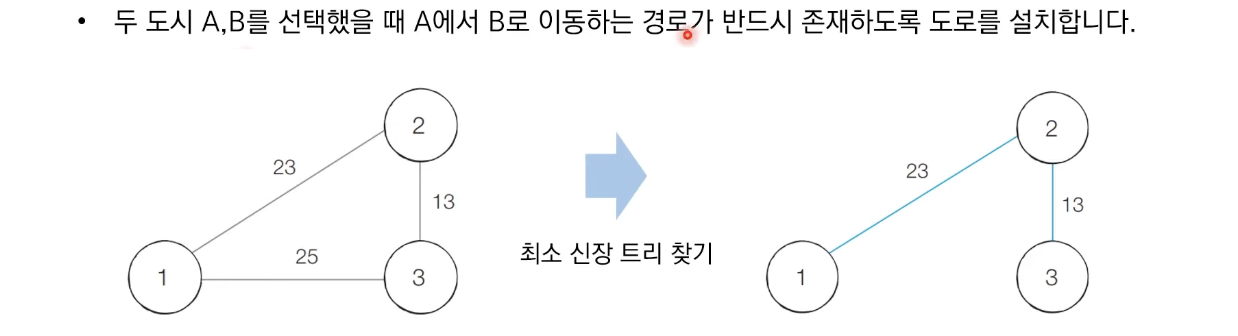
- 최소한의 비용으로 구성되는 신장 트리를 찾아야 할 때 어떻게 해야 할까?
- 예를 들어 N개의 도시가 존재하는 상황에서 두 도시 사이에 도로를 놓아, 전체 도시가 서로 연결 될 수 있게 도로를 설치하는 경우를 생각해 보자.
크루스칼 알고리즘
- 대표적인 최소 신장 트리 알고리즘이다.
- 그리디 알고리즘으로 분류된다.
- 구체적인 동작 과정은 다음과 같다.

크루스칼 알고리즘: 동작 과정 요약
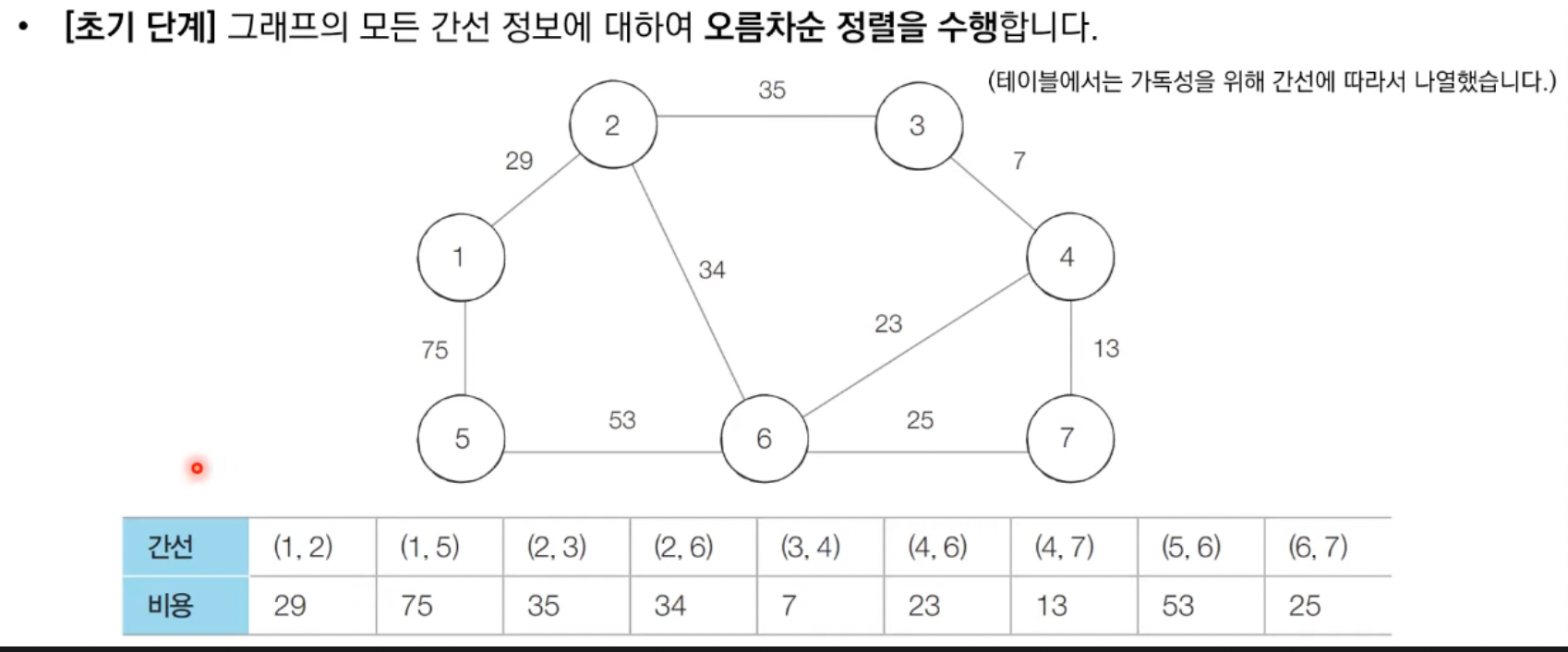
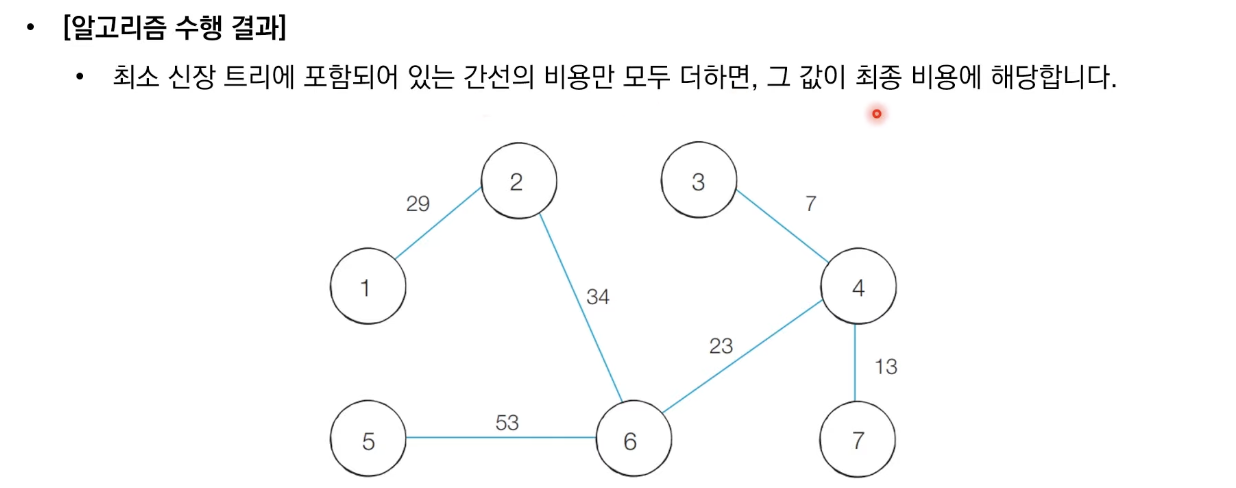
입력 예시
7 9
1 2 29
1 5 75
2 3 35
2 6 34
3 4 7
4 6 23
4 7 13
5 6 53
6 7 25
- 첫번째 줄에 vertext와, 간선의 개수가 주어진다.
- 간선의 개수만큼, "출발 도착 cost"로 구분되어 입력한다.
출력 예시
159
- 크루스칼 알고리즘
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드를 찾을 떄까지 재귀 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(Union 연산)의 개수 입력 받기
v, e = map(int, input().split())
# 부모 테이블 초기화하기
parent = [0] * (v + 1)
# 모든 간선을 담을 리스트와, 최종 비용을 담을 변수
edges = []
result = 0
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
# 모든 간선에 대한 정보를 입력 받기
for _ in range(e):
a, b, cost = map(int, input().split())
# 비용순으로 정렬하기 위해서, 튜플의 첫 번재 원소를 비용으로 설정
edges.append((cost, a, b))
# 간선을 비용순으로 정렬
edges.sort()
# 간선을 하나씩 확인하며
for edge in edges:
cost, a, b = edge
# 사이클이 발생하지 않는 경우에만 집합에 포함
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
result += cost
print(cost)위상 정렬
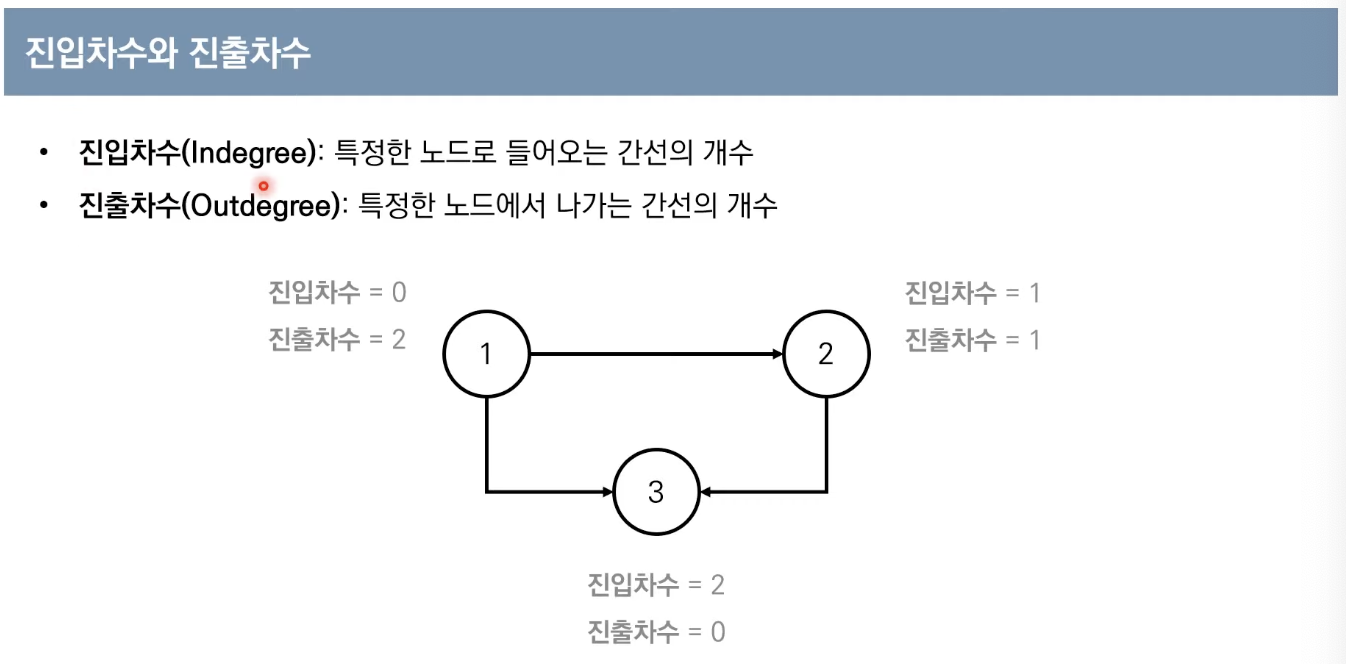
- 사이클이 없는 방향 그래프의 모든 노드를, 방향성에 거스르지 않도록 순서대로 나열하는 것을 의미한다.
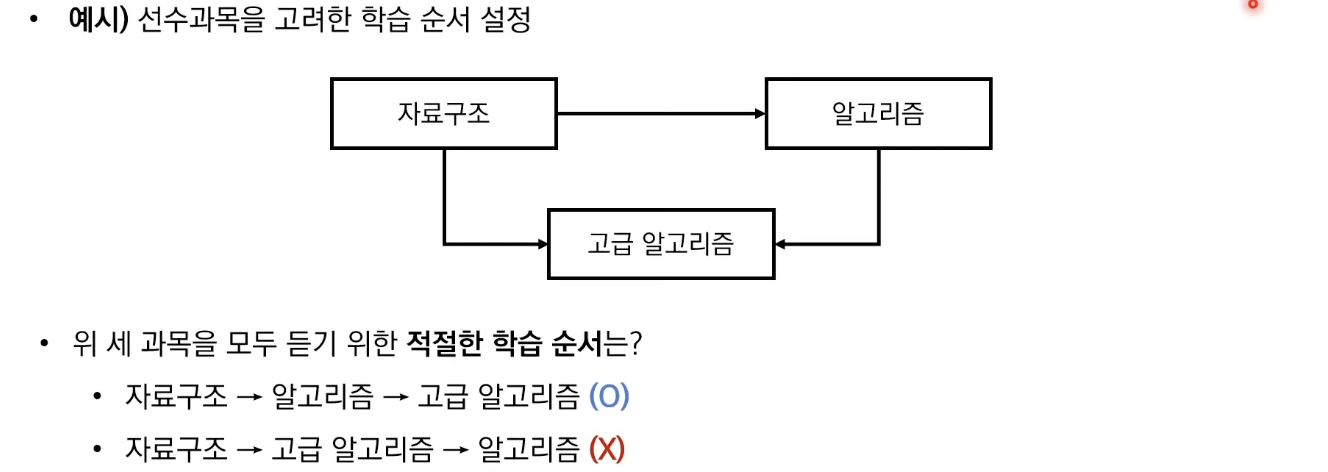
위상 정렬 알고리즘
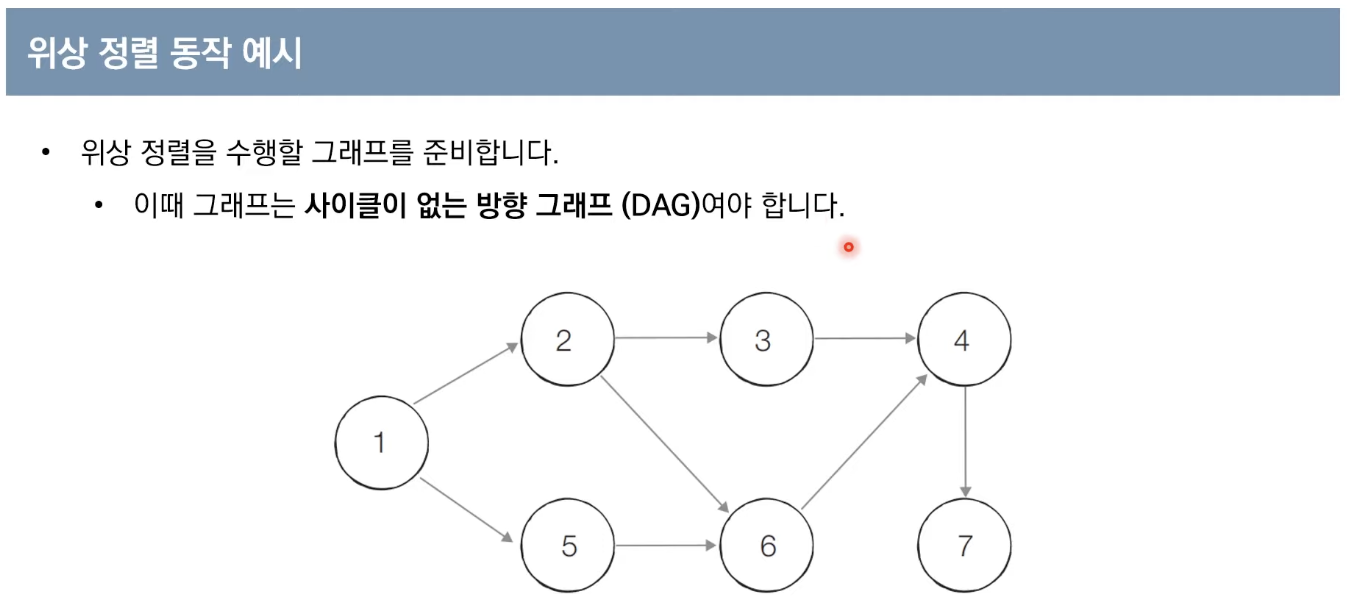
- 큐를 이용하는 위상 정렬 알고리즘의 동작 과정은 다음과 같다.

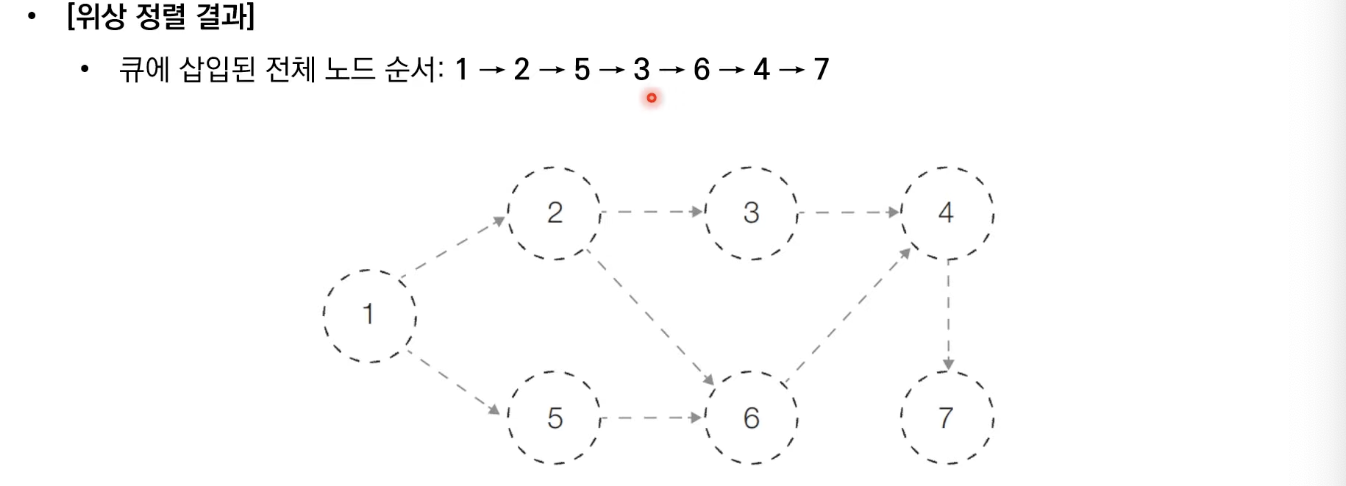
위상 정렬의 특징

입력 예시
7 8
1 2
1 5
2 3
2 6
3 4
4 7
5 6
6 4
출력 예시
1 2 5 3 6 4 7
from collections import deque
# 위상 정렬 함수
def topology_sort():
# 알고리즘 수행 결과를 담을 리스트
result = []
# 큐 기능을 위한 deque 라이브러리 사용
q = deque()
# 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for i in range(1, v + 1):
if indegree[i] == 0:
q.append(i)
# 큐가 빌때까지 반복
while q:
# 큐에서 원소 꺼내기
now = q.popleft()
result.append(now)
# 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for i in graph[now]:
indegree[i] -= 1
if indegree[i] == 0:
q.append(i)
return result
# 노드의 개수와 간선의 개수를 입력 받기
v, e = map(int, input().split())
# 모든 노드에 대한 집입차수는 0으로 초기화
indegree = [0] * (v + 1)
# 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
graph = [[] for _ in range(v + 1)]
# 방향 그래프의 모든 간선 정보를 입력 받기
for _ in range(e):
a, b = map(int, input().split())
# 정점 A에서 B로 이동 가능
graph[a].append(b)
# 진입 차수를 1 증가
indegree[b] += 1
result = topology_sort()
# 위상 정렬을 수행한 결과 출력
for i in result:
print(i, end=' ')