코딩 테스트를 위한 벨만 포드 알고리즘 7분 핵심 요약

• 이것이 취업을 위한 코딩테스다 with 파이썬(이코테 2021) 유튜브 영상을 보면서 공부한 자료입니다.
• https://www.youtube.com/watch?v=m-9pAwq1o3w&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC

---

음수 간선이 포함된 상황에서의 최단 거리 문제

벨만 포드 최단 경로 알고리즘

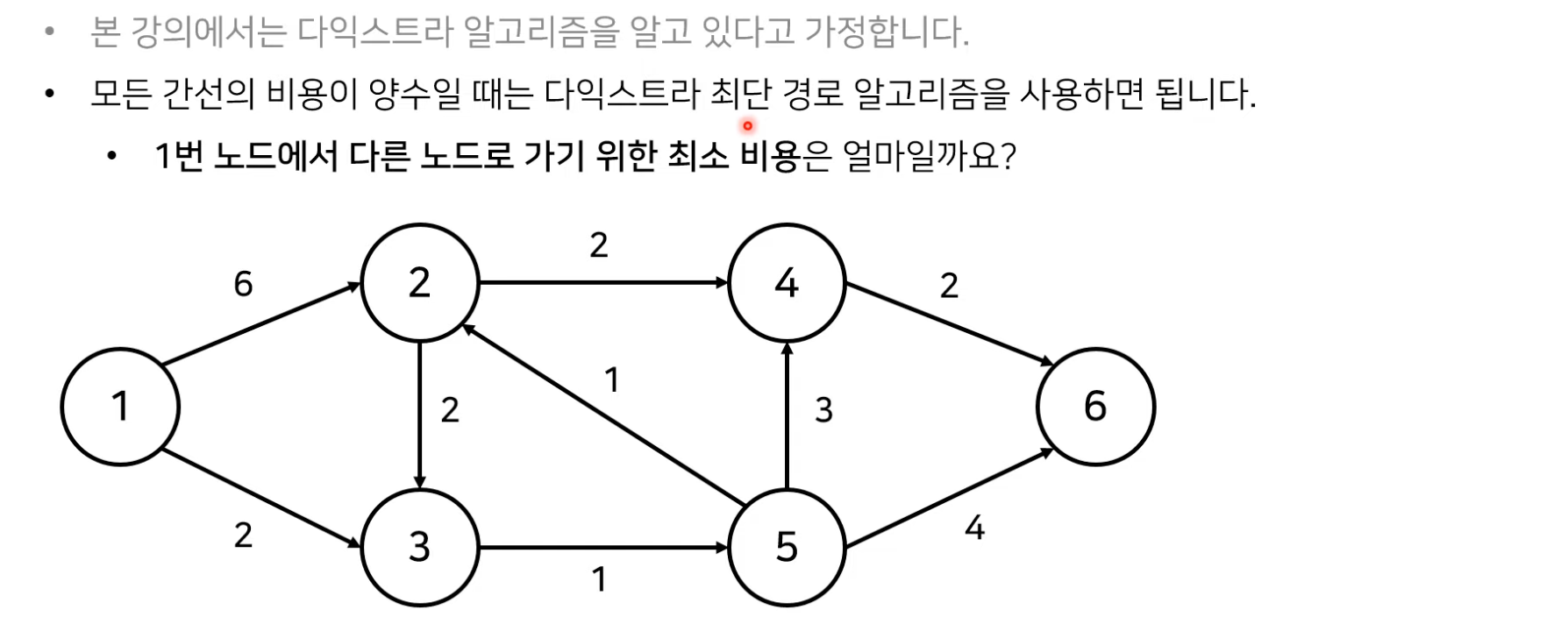
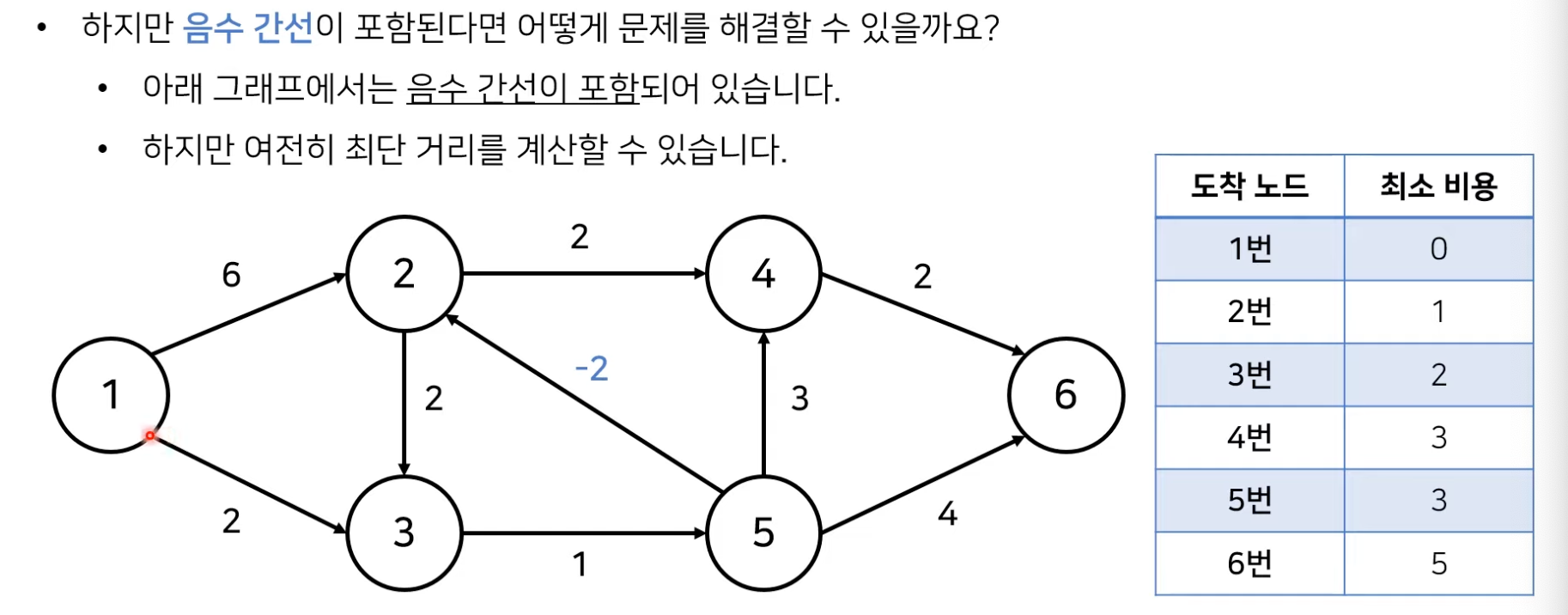
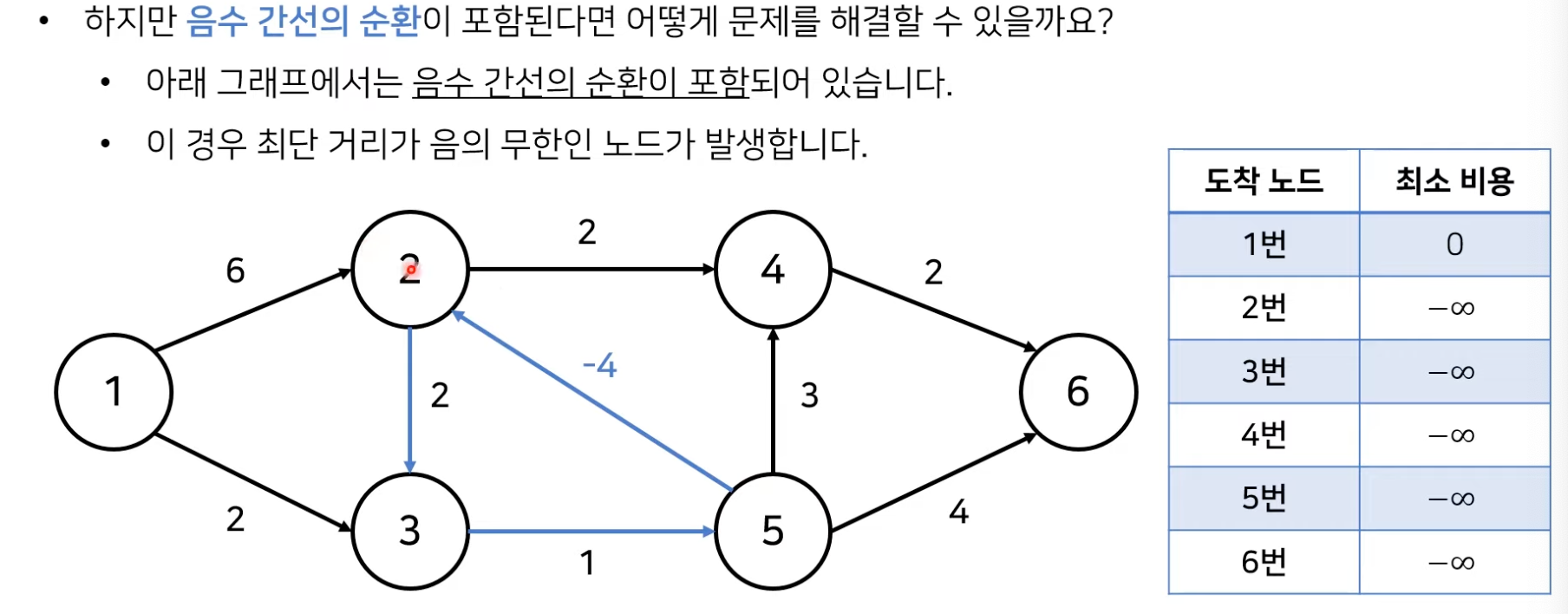
• 음수 간선에 관하여 최단 경로 문제는 다음과 같이 분류할 수 있다.

• 벨만 포드 최단 경로 알고리즘은, 음의 간선이 포함된 상황에서도 사용할 수 있다.

벨만 포드 알고리즘 vs 다익스트라 알고리즘

import sys
input = sys.stdin.realine
INF = int(1e9)

def bf(start):
    # 시작 노드에 대해서 초기화
    dist[start] = 0
    # 전체 n번의 라운드(round)를 반복
    for j in range(n):
        cur = edges[j][0]
        next_node = edges[j][1]
        cost = edges[j][2]
        # 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
        if dist[cur] != INF and dist[next_node] > dist[cur] + cost:
            dist[next_node] = dist[cur] + cost
            # n번째 라운드에서도 값이 갱신된다면 음수 순환이 존재
            if i == n - 1:
                return True
    return False

# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 모든 간선에 대한 정보를 담는 리스트 만들기
edges = []
# 최단 거리 테이블을 모두 무한으로 초기화
dist = [INF] * (n + 1)

# 모든 간선 정보를 입력받기
for _ in range(m):
    a, b, c = map(int, input().split())
    # a번 노드에서 b번 노드로 가는 비용이 c라는 의미
    edges.append((a, b, c))

# 벨만 포드 알고리즘 수행
# 1번 노드가 시작 노드
negative_cycle = bf(1)

if negative_cycle:
    print("-1")
else:
    # 1 번 노드를 제외한 다름 모든 노드로 가기 위한 최단 거리 출력
    for i in range(2, n + 1):
        # 도달할 수 없는 경우, -1을 출력
        if dist[i] == INF:
            print("-1")
        # 도달할 수 있는 경우 거리를 출력
        else:
            print(dist[i])