- 출처
- 핸즈온 머신러닝2
- 핸즈온 머신러닝2 github
- 핸즈온 머신러닝2 4장 pdf
- 되도록이면 책의 내용과 코드를 그대로 옮기기 보다는 요약과 보충설명!
읽기전에
개념 정리
벡터 사이의 점곱
열벡터(열행렬)
: 한 개의 열을 갖는 행렬
- 어떤 행벡터 a와 열벡터 b가 있을 경우, 이 두 행렬의 곱은 두 벡터의 내적의 값과 같다
유사 역행렬?
: 역행렬이 존재하지 않는 경우 부분적으로 역행렬과 유사한 역할을 할 수 있는 행렬
- 또는 어떤 특성이 중복되어 역행렬이 없다면(특이 행렬일 경우), 정규방정식은 작동하지 않지만 유사역행렬은 항상 구할 수 있음
특잇값 분해(singualar value decomposition(SVD))
: 표준 행렬 분해 기법으로, 이것을 사용해서 유사역행렬을 계산.
편향/분산 트레이드 오프
- 모델의 복잡도가 커지면, 분산이 늘어나고 편향이 줄어듬.
- 모델의 복잡도가 작아지면, 분산이 작아지고 편항이 커짐.
편향
: 잘못된 가정으로 인해 발생.
- 편향이 크면 과소적합 가능성도 커짐
분산
: 훈련 데이터의 작은 변동에 모델이 과도하게 민감할때 발생
- 자유도가 높은 모델(고차 다항 회귀 모델 등..)은 과대적합 가능성이 커짐(높은 분산을 가지기 쉽기 때문에)
줄일 수 없는 오차(irreducible error)
: 데이터 자체에 있는 잡음 때문에 발생
크로스 엔트로피(정리해야함)
4장 모델 훈련
- 우리가 구현의 모든 내용을 다 알아야 하는건 아니지만, 원리를 알면 많은 이점이 있다
- 적절한 모델, 올바른 훈련 알고리즘, 작업에 맞는 좋은 하이퍼파라미터를 빨리 찾을 수 있다
- 디버깅이나 에러 분석시 효율적이다
선형 회귀로 해보자
- : 예측값, : 특성의 수, : 번째 특성값, : j번째 모델 파라미터
: 벡터 형태 (더보기)
비용 함수
: RMSE보다 MSE가 더 간단하므로, 사용
정규방정식: 비용 함수 최소화
- 정규방정식(nomal equation)
- : 비용 함수를 최소화하는
- : 부터 y^{(m)} 까지 포함하는 타깃 벡터
정규방정식으로 계산
- numpy 선형대수 모듈(np.linalg)의
inv()로 역행렬 계산,dot()으로 행렬 곱셈
무어-펜로즈 유사 역행렬 계산
LinearRegression 클래스의scipy.linalg.lstsq()함수
: 계산- 또는
np.linalg.pinv()로 유사 역행렬 직접 구하기 가능
계산 복잡도
- 정규방정식으로 역행렬 계산시, 계산 복잡도는 에서 $O(n^{3}) 사이.
- 사이킷런
LinearRegression의 SVD로 유사역행렬 계산시, 계산 복잡도는
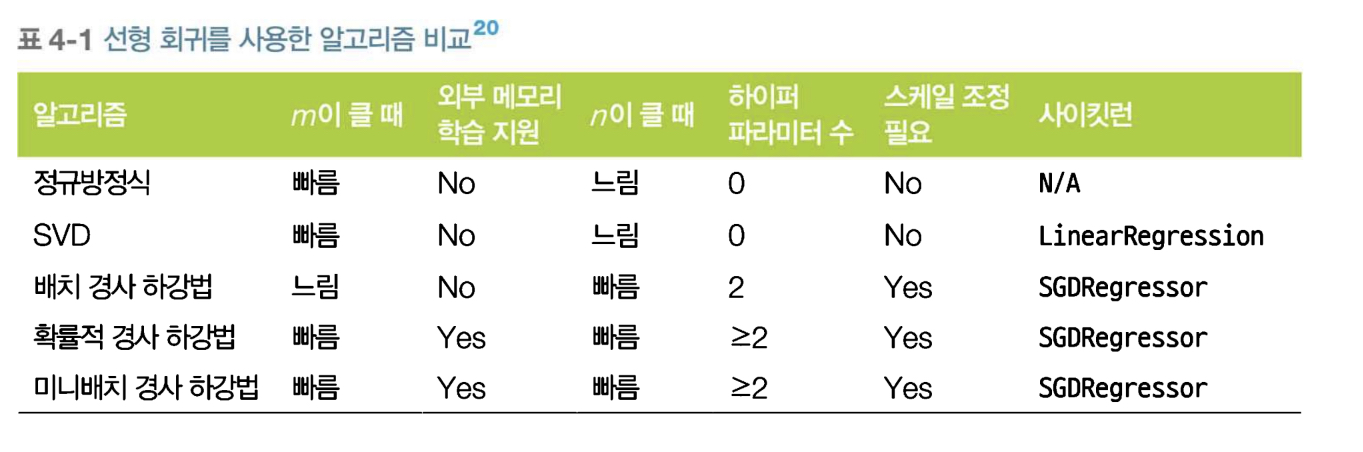
경사 하강법의 종류
경사 하강법
: 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘.
: 비용 함수를 최소화 하기 위해서 방복해서 파라미터를 조정해 나감.
- 허용오차를 정하여, 벡터의 노름이 그 값보다 작아지면 알고리즘을 중지.
경사 하강법의 문제점
- 학습률 파라미터(스텝의 크기)가 너무 작으면, 시간이 오래 걸리고
학습률 파라미터가 크면, 발산한다. - 무작위 초기화(임의의 로 시작하기 때문에, 전역 최솟값보다 덜 좋은 지역 최솟값에 수렴하는 문제가 발생 가능
배치 경사 하강법
: 매 경사 하강법 스텝에서 전체 훈련 세트를 사용하여 그레디언트를 계산한다.
배치 경사 하강법의 문제점
- 매우 큰 훈련 세트에서는 엄청 느리다.
확률적 경사 하강법(SGD)
: 매 스텝 한 개의 샘플을 무작위로 선택하여 그 하나의 샘플에 대한 그레디어트를 계산 함.
- 사이킷런에서
SGDRegressor 클래스로 선형회귀 가능
확률적 경사 하강법 문제점
: 그냥 경사 하강봅보다는 훨씬 불안정 하다. 구해진 최솟값이 최적치가 아닐 수 있다.
- 이를 해결하기 위해, 학습 스케줄로 점진적으로 학습률을 줄일 수 있다.
미니배치 경사 하강법
: '미니배치'라는 임의의 작은 샘플 세트에 대해 그레디언트를 계산.
- GPU를 사용해서 얻는 성능 향상
- 미니배치가 어느정도 크면, SGD보다 덜 불규칙하게 움직임.
- 최솟값에 더 가까이 도달하지만, 지역 최솟값에 빠질 확률은 커짐
다항 회귀는 어떨까?
- 비선형 데이터를 학습하는데 선령 모델을 사용할 수 있다.
- 고차 다항 회귀는 과대 적합될 가능성이 크다.
학습 곡선: 모델의 복잡도 결정 및 과대/과소적합 판단
모델의 복잡도 결정 및 과대/과소적합 판단
- 교차 검증
- 학습 곡선 살펴보기
학습 곡선
: 훈련 세트와 검증 세트의 모델 성능을 훈련 세트 크기(또는 훈련 반복)의 함수로 나나냄.
- 훈련 세트에서 크기가 다른 서브 세트를 만들어 모델을 여러 번 훈련시킴
과소적합 되었다면
: 더 복잡한 모델을 선택하거나 더 나은 특성을 선택해야함
- 훈련 샘플을 추가하는건 효과 없음
과대적합 되었다면
: 훈련 샘플을 더 추가하기. 모델을 규제하기.
규제가 있는 선형 모델
과대적합 감소시키기
- 자유도 줄이기
- 다항식의 차수 감소(다항 회귀 모델일 경우)
- 모델의 가중치를 제한
릿지 회귀(ridge 회귀, 티호노프(Tikhonov) 규제)
: 규제가 추가된 선형 회귀 버전
- 비용 함수에 규제항 이 추가됨
- 릿지 회귀의 비용 함수:
- 훈련이 끝나고 모델의 성능 평가시에는 규제가 없는 성능 지표로 평가
- 모델의 가중치가 가능한 한 작게 유지되도록 함.
- : 하이퍼파라미터.
- 클수록 모델의 분산은 줄어들고, 편향은 커짐.
- 아주 클수록 모든 가중치가 거의 0에 가까워지고, 데이터의 평균을 지나는 수평선이 됨
- 작을수록 선형회귀와 가까짐
라쏘 회귀(Lasso 회귀)
: 규제가 추가된 선형 회귀 버전.
-
비용 함수에 규제항이 추가됨
-
라쏘 회귀의 비용 함수:
-
덜 중요한특성의 가중치를 제거(가중치가 0이 됨). 즉 0이 아닌 특성의 가중치가 적으므로, 자도으로 특성 선택을 하고 희소 모델을 만드는 셈.
-
일 떄 미분이 안되지만, 서브그레이디언트 벡터 을 사용하면 경사 하강법을 적용 가능하다.
엘라스틱넷
: 릿지 회귀와 라쏘 회귀를 절충한 모델
- 엘라스틱넷 비용 함수:
- : 0이면 릿지 회귀가, 1이면 라쏘 회귀가 됨.
어떤 규제 방법이 좋은 방법일까?
- 우선, 규제가 없는건 피하자!
- 릿지가 기본
- 그러나, 왜인지 쓰이는 특성이 몇개 뿐이다? 라쏘나 엘라스틱넷을 쓰자
- 또는 특성 수가 훈련 샘플 수보다 많거나 특성 몇 개가 강하게 연관되어 있을 때는 엘라스틱넷을 쓰자
조기 종료
- 검증 에러가 최솟값에 도달하면 바로 조기 종료하자. 그렇지 않으면, 과대적합 될 것이다.
로지스틱 회귀(로짓 회귀)
: 분류에서도 사용 가능
- 이진분류기: 1이면 양성 클래스, 0이면 음성 클래스로 예측
확률 추정
- 입력 특성의 가중치 합을 계싼하여 로지스틱을 출력: 시그모이드 함수
훈련과 비용 함수
- 로지스틱 회귀의 비용 함수:
- 볼록 함수 이므로, 경사 하강법 등을 이용하여 전역 최솟값을 구하면 됨. 정규방정식은 존재하지 않음.
소프트맥스 회귀(다항 로지스틱 회귀)
: 여러 개의 이진 분류기를 훈련시켜 연결하지 않고도 직접 다중 클래스를 지원하도록 일반화 될 수 있다.
- 샘플 x에 대해서 소프트 맥스 회귀 모델이 각 클래스 k에 대한 점수를 계산하고, 그 점수에 소프트맥스 함수(정규화된 지수 함수)를 적용하여 각 클래스의 확률을 추정.
- 추정 확률이 가장 높은 클래스(쯕, 점수가 가장 높은 것)을 선택
궁금증
- 과소적합, 과대적합을 구분하는 방법은?
: f1 score나 정확도 등 모델 평가를 하는데 기준이 되는 값을 그래프로 그려봤을 때, 어떤 때를 기점으로 확 성능이 좋아진다면 과대적합을 의심할 수 있다.
: RMSE 값 같은 경우는 정확도가 분류기의 성능 측정 지표로 선호되지 않는 것과 유사하게 잘 선호되지 않음.