• 출처
  • 핸즈온 머신러닝2
  • 핸즈온 머신러닝2 github
  • 핸즈온 머신러닝2 5장 pdf
• 되도록이면 책의 내용과 코드를 그대로 옮기기 보다는 요약과 보충설명!

읽기전에

개념 정리

• 참고: https://sonsnotation.blogspot.com/2020/11/11-1-kernel.html
• 참고: https://bskyvision.com/163

python 정리

3장

• 서포트 벡터 머신(SVM, Support Vector Machine)
• 복잡한 분류 문제, 작거나 중간 크기의 데이터셋에 적합

선형 SVM 분류

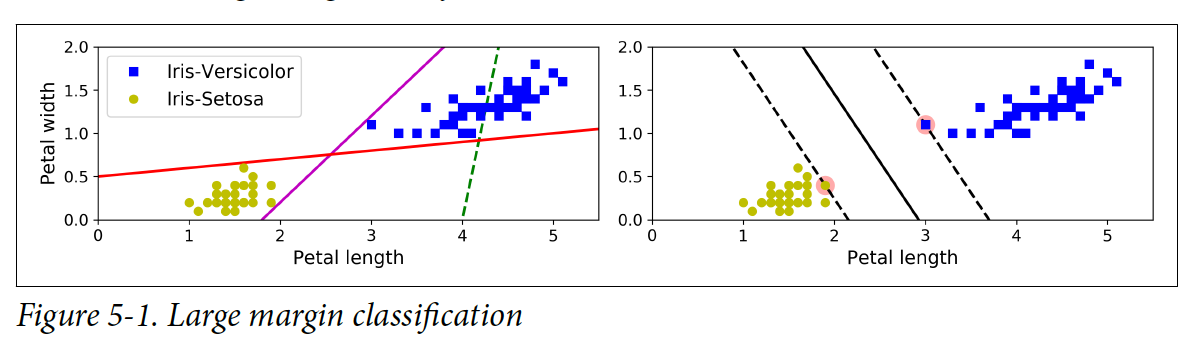
라지 마진 분류

: 마치 클래스 사이에 가장 폭이 넓은 도로를 찾는 느낌.

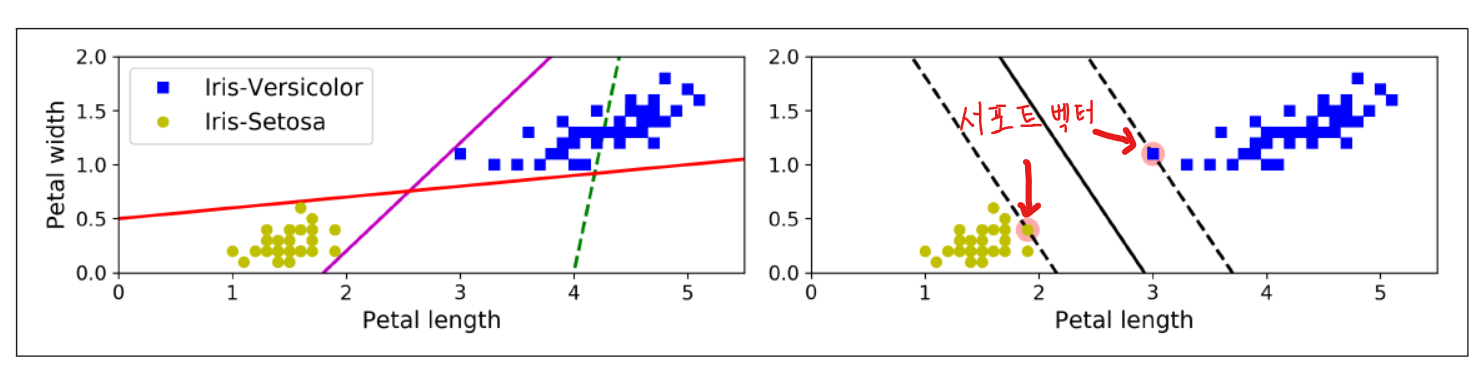
• 서포트 벡터(support vector)
  : 도로 경계에 위치한 샘플
• 특성의 스케일에 민감
  : 단위가 클 때는 작은 차이가 잘 느껴지지 않아 도로가 좁아지지만, 단위가 작을 때는 작은 차이도 크게 느껴져서 도로가 넓어짐
  : 사이킷런의 StandardScaler로 특성의 스케일 조정 가능

하드 마진 분류

: 모든 샘플이 도로 바깥쪽에 올바르게 분류되어 있을때. 즉 마진 오류가 하나도 없음

• 문제점
  1. 데이터가 선형적으로 구분될 때 작동함
  2. 이상치에 민감함

소프트 마진 분류

: 도로의 폭을 넓게 유지하려는 것과 마진 오류(샘플이 도로 중간 혹은 반대쪽이 있는 경우) 사이의 균형 잡기. 즉 제한적인 마진 오류를 가짐

마진의 넓이와 하이퍼파라미터 조정

• 하이퍼파라미터 C가 크면 -> 도로가 좁아짐 -> 과대적합 가능성 상승
• 하이퍼파라미터 C가 작으면 -> 도로가 넓어짐 -> 과소적합 가능성 상승

선형 SVM 모델 훈련하기

사용 모델	방법
LinearSVC	힌지손실 함수를 적용
SVC 클래스	선형 커널 사용
SGDClassifier 모델	확률적 경사 하강법

비선형 SVM 분류

다항 특성 방식

• PolynomialFeatures 변환기와 StandardScaler, LinearSVC을 연결하여 Pipeline 만들기
• 단점
  • 낮은 차수의 다항식: 매우 복자한 데이터셋을 잘 표현하지 못함
  • 높은 차수의 다항식: 모델이 느려짐

다항식 커널

• 커널 트릭 사용: 실제로는 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 같은 결과를 얻음

유사도 특성

• 각 샘플이 특정 랜드마크와 얼마나 닮았는지 측정하는 유사도 함수로 계산한 특성을 추가.
• 가우시안 RBF(방사 기저 함수)
  : 0(랜드마크에서 아주 멀리 떨어진 경우) ~ 1(랜드마크와 같은 위치)로, 종 모양

가우시안 RBF 커널

• 커널 트릭 사용: 유사도 특성을 많이 추가하는 것과 비슷한 결과를 얻음

커널 선택

: 선형 커널을 먼저 시도하기.

• LinearSVC가 SVC(kernel="linear"보다 훨씬 빠름

계산 복잡도

• LinearSVC 파이썬 클래스: 선형 SVM을 위한 최적화된 알고리즘을 구현한 liblinear 라이브러리 기반
• SVC: 커널 트릭 알고리즘을 구현한 libsvm 라이브러리기반

사용 모델	방법	시간 복잡도
LinearSVC	힌지손실 함수를 적용	$O(m\times n)$
SVC 클래스	선형 커널 사용	$O(m^2 \times n)$과 $O(m^3\times n)$ 사이
SGDClassifier 모델	확률적 경사 하강법	$O(m\times n)$

SVM 회귀

• SVM 분류와는 반대로, 제한된 마진 오류(즉, 도로 밖의 샘플) 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 학습
• 그니까.. 회귀선에 모여 있을수록 좋잖아? 그거 생각하면 됨
• $\varepsilon$에 민감하지 않음: 훈련 샘플의 추가가 모델의 예측에 영향을 주지 않음

커널 SVM

• 비선형 회귀

SVM 이론

결정 함수와 예측

• 선형 SVM 분류기를 훈련한다
  = 하드 마진 혹은 소프트 마진 분류에서 가능한 한 마진을 크게하는 $\mathbf{w}$와 $b$를 찾는 것.

목적 함수

• 가중치 벡터$\mathbf{w}$가 작을수록 마진은 커짐

콰드라틱 프로그래밍(QP) 문제

: 선형적인 제약 조건이 있는 볼록 함수의 이차 최적화 문제. 하드 마진과 소프트 마진은 이에 해당.

쌍대 문제

• SVM은 쌍대 문제의 해가 원 문제의 해와 같아지는 조건을 만족하기 때문에, 원 문제 또는 쌍대 문제 중 하나를 선택하여 풀 수 있음.

커널 SVM

온라인 SVM

• 경사 하강법: 느림
• QP 기반의 방법

궁금증

1. 213p. 유사도 특성의 개념은 알겠는데.. 이게 왜 유용한지는 모르겠다. 작동원리도 잘 이해가 안됨. 예시가 더 있었으면 좋겠다.
2. 217p. 그림 5-11의 두 그림이 잘 구분되지 않습니다. 규제의 정도에 따른 차이가 별로 없어 보입니다. 이정도 규제 차이로는 체감이 안 된다고 해석해야할지, 아니면 이 그래프가 유독 구별이 덜 되는건지 모르겠네요.