• 에이블 교육 정리

정리

원리, 개념

• 정보 증가량이 가장 큰 변수를 기준으로 split 하기를 반복한다

전제조건

• NaN 조치, 가변수화

성능

• max_depth가 클수록, min_samples_leaf가 작을수록 모델이 복잡하다

원리

불순도

지니 불순도(Gini Impurity)

• 범위: 0~0.5
  $Gini = 1- \displaystyle \sum_{i=1}^c (p_i)^2$
• 예:

  • 몸통

    • 네모의 지니 불순도: $\displaystyle 1-((\frac{5}{6})^2+(\frac{1}{6})^2)=0.833$

    • 타원의 지니 불순도: $\displaystyle 1-((\frac{2}{6})^2+(\frac{4}{6})^2)=0.167$

    • 몸통의 지니 불순도: $\displaystyle\frac{6}{12} \times 0.833 + \frac{6}{12} \times 0.167 = 0.361$: 가중평균!!

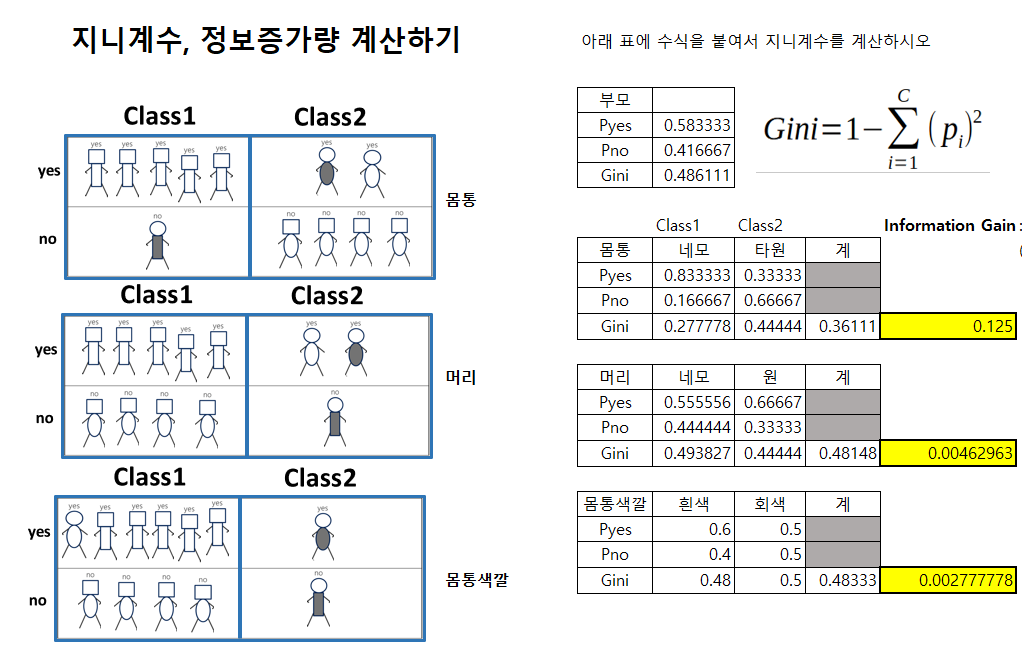
• 출처: 한기영 강사님 실습자료

엔트로피

• 범위: 0~1

정보 증가량(Information Gain)

• = 정보 증가량, 정보 전달량, 정보 획득량
  : 얼마나 불순도를 해결한거야, 얼마나 yes no 분류하는데 영향을 준거야
• 부모의 불순도 - 자식의 불순도
• tree가 분기될 때, 가장 정보 증가량이 큰 변수부터 기준이 됨.
• 예:
  • 전체 불순도: 0.486
  • 몸통의 불순도: 0.361
  • 정보 증가량: 0.125

Feature Importance(변수 중요도, 특성 중요도)

: 모델 전체에서 각 feature별 정보이득의 합을 정규화시킨 값

• 특성 중요도를 다 더하면 합계가 1.

단점

• 편향적이다.
• 즉, 연속형 변수 또는 카테고리 개수가 매우 많은 변수, 즉 ‘high cardinality’ 변수들의 중요도를 더욱 부풀릴 가능성이 높다

정보증가량과 변수 중요도의 차이?

정보증가량의 순서와 변수 중요도의 순서가 일치하지 않는다??

• 예: A가 가장 변수 중요도가 큰데, 왜 B가 정보증가량이 큰 변수로 나올까?
• 부모의 불순도를 가장 떨어트려주는 변수(즉, 정보 획득량이 가장 많은 변수)부터 분기로 나눔.
• 그러나 특성 중요도는 모델의 전체로 확장하여서 판단한 것.
• 그렇기 때문에 둘이 일치하지 않을 수 있다.

특징

장점

• 화이트박스 모델이다: 분석 과정을 한눈에 시각화 가능
• 직관적, 이해하기 쉬움
• 빠르다?
• 회귀, 분류 둘다 가능

단점

하이퍼파라미터

max_depth

: 경로의 길이

• 최대 깊이가 클수록 모델이 복잡하다. 트리 크기가 커진다.

min_samples_leaf

: leaf node의 data의 최소 건수

• 리프 노드의 최소 건수가 작을수록 모델이 복잡하다. 트리 크기가 커진다.