Bubble Sort

교환 정렬

인접한 두 element를 비교한 후 교환

특징

• element 이동이 거품이 수면으로 올라오는 듯한 모습을 보이는 정렬
• 시간 복잡도: O(n^2)
• 코드가 단순하지만 비효율적

방법

• 0번째 vs 1번째 비교 -> 오른쪽 값이 작다면 교환
• 1번째 vs 2번째 비교
• ...
• 다시 0번째 vs 1번째 비교
• n개 원소라면 n-1 번의 회전
  
  

Selection Sort

선택 정렬

정렬하지 않은 값 중 최소 값을 찾아서 현재 자리와 교환

특징

• 제자리 정렬 알고리즘
• 시간 복잡도: O(n^2)
• 같은 값이 있는 경우 두 값의 위치를 보장할 수 없다 = 안전하지 않은 정렬
• 코드가 단순하지만 비효율적

방법

• 최소값을 찾은 후 0번째와 교환
• 0번째 이후 숫자에서 최소값을 찾은 후 1번째와 교환
  ...
• n-2 번째 이후 숫자에서 최소값을 찾은 후 n-1 번째와 교환
  
  

Insertion Sort

삽입 정렬

이미 정렬된 부분과 비교하여 자신의 위치를 찾아 삽입

특징

장점

• 안전한 정렬
• 대부분의 요소가 이미 정렬된 경우 효율적

단점

• 요소 수가 적을 경우 복잡한 알고리즘 보다 유리하지만 크기가 큰 경우 적합하지 않다
  
  

시간 복잡도

• 최선: O(n) - 이미 정렬된 경우
• 평균: O(n^2)
• 최대: O(n^2) - 역순으로 정렬된 경우

방법

• 1번째를 0번째와 비교 후 올바른 위치에 삽입
• 2번째를 0~1과 비교 후 올바른 위치에 삽입
  ...
• n번째를 0~n-1과 비교 후 올바른 위치에 삽입

Quick Sort

교환 정렬

pivot을 기준으로 정렬한 후 다시 왼쪽, 오른쪽을 퀵 정렬 후 병합

• 분할 정복 알고리즘 - 문제를 작은 문제로 분리한 후 모아서 문제를 해결

특징

• pivot은 중간 크기의 값이 좋음

장점

• 속도가 빠르다
• 추가 메모리 공간을 필요로 하지 않는다.

단점

• 이미 정렬이 된 경우 오히려 수행시간이 더 걸린다
  
  

시간 복잡도

• 최선: O(nlogn)
• 평균: O(nlogn)
• 최대: O(n^2)
  
  

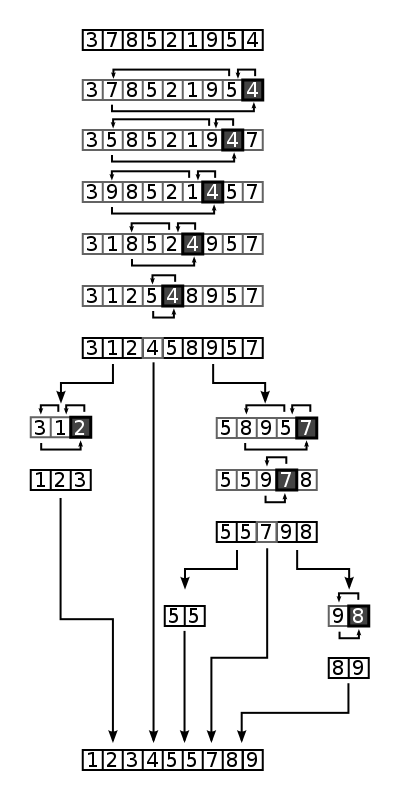
방법

• 임의의 값을 pivot으로 선택
• 왼쪽(left)과 오른쪽(right)부터 pivot과 값을 비교
• 왼쪽 값이 pivot 보다 크고, 오른쪽 값이 pivot 보다 작으면 교환
• left와 right가 서로 만나면 해당 위치에 pivot을 삽입
• pivot을 기준으로 왼쪽, 오른쪽을 다시 quick 정렬 실행

---

참고 링크
위키피디아 - 버블 정렬
버블 정렬
위키피디아 - 선택 정렬
선택 정렬
위키피디아 - 삽입 정렬
삽입 정렬
위키피디아 - 퀵 정렬
퀵 정렬