1. Merge Sort
부분 리스트로 분할한 후 정렬하며 하나의 리스트로 병합
시간 복잡도
- 최선, 평균, 최악: O(nlogn)
특징
- 비교 기반 알고리즘
- 분할 정복 알고리즘
- 안정한 정렬
방법
- 정렬되지 않은 리스트를 n개의 부분 리스트로 분할
- 부분 리스트를 정렬한 후 병합
- 하나의 리스트로 병합될 때까지 정렬 및 병합
코드
func mergeSort(_ array: [Int]) -> [Int] {
guard array.count > 1 else { return array } // 부분 리스트의 요소가 하나 이상인지 확인
let midIndex = array.count / 2
let leftArray = Array(array[0..<midIndex])
let rightArray = Array(array[midIndex..<array.count])
// 가운데를 기준으로 왼쪽, 오른쪽 부분 리스트로 나눔
return merge(left: mergeSort(leftArray), right: mergeSort(rightArray))
// 나눈 부분 리스트를 다시 merge sort하면서 병합
}
// 병합하는 함수
func merge(left: [Int], right: [Int]) -> [Int] {
var result: [Int] = [] // 병합할 배열
var i = 0, j = 0
while i < left.count && j < right.count {
if left[i] < right[j] { // 왼쪽, 오른쪽 부분 리스트 요소를 하나씩 비교
result.append(left[i]) // 더 작은 값을 병합하는 배열에 추가
i += 1
} else {
result.append(right[j])
j += 1
}
}
// 부분 리스트의 개수가 다르면 하나가 남음
if i < left.count { // 병합되지 않은 요소가 남아있으면 추가
result.append(left[i])
}
if j < right.count {
result.append(right[j])
}
return result
}2. Heap Sort
최소 힙 트리 또는 최대 힙 트리를 구성해 정렬
시간 복잡도
- 최선, 평균, 최악: O(nlogn)
특징
- 최소 힙 트리 -> 내림차순 정렬 / 최대 힙 트리 -> 오름차순 정렬
방법
- 왼쪽 노드, 오른쪽 노드를 가진 완전 이진 트리로 표현
- 최대 힙을 구성 (부모 노드가 자식 노드보다 큰 값을 가지는 트리)
- 루트 노드(가장 큰 수)를 마지막 노드와 교환
- 마지막 노드를 제외하고 2와 3을 반복
Array에서 Heap 표현
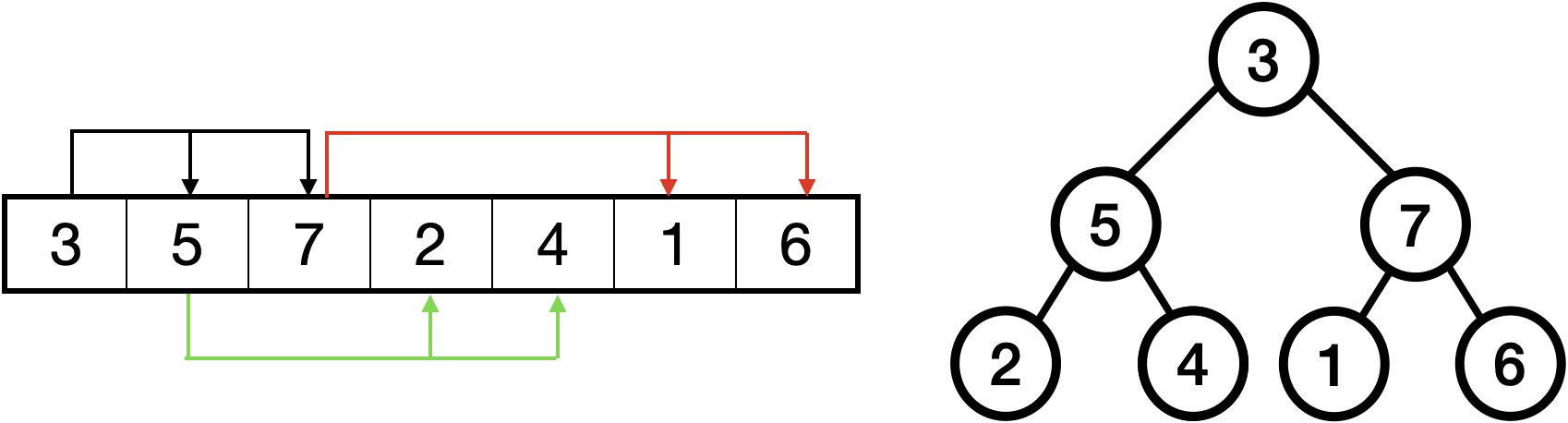
자식 노드 찾기
0번째 -
왼쪽 노드 - 1번째|오른쪽 노드 - 2번째
1번째 -왼쪽 노드 - 3번째|오른쪽 노드 - 4번째
2번째 -왼쪽 노드 - 5번째|오른쪽 노드 - 6번째
...
n번째 -왼쪽 노드 - 2n+1번째|오른쪽 노드 - 2n+2번째
부모 노드 찾기
n번째 부모노드 = (n-1)/2번 노드
코드
func heapSort(_ array: [Int]) -> [Int] {
var arr = array
for i in stride(from: array.count - 1, to: -1, by: -1) {
arr = makeMaxHeap(arr, i) // 이미 정렬된 부분은 빼고 최대 힙으로 구성
arr.swapAt(0, i) // 마지막 노드와 루트 노드를 swap -> 가장 큰수를 마지막으로
}
return arr
}
// 최대 힙으로 만드는 함수
func makeMaxHeap(_ array: [Int], _ maxIndex: Int) -> [Int] {
var arr = array
for j in stride(from: maxIndex, to: 0, by: -1) { // 마지막 노드부터 비교
if arr[j] > arr[(j-1)/2] { // 부모 노드와 비교
arr.swapAt(j, (j-1)/2) // 부모 노드보다 크면 swap
}
}
return arr
}3. Radix Sort
기수에 따라 element를 버켓에 집어 넣어 정렬
-> 기수: 정수, 낱말 등 크기가 유한하고 사전순으로 정렬할 수 있는 자료
시간 복잡도
- 최악 : O(w(k + n))
- w: 기수의 크기, k: 기수의 도메인 크기
특징
- 최상위 유효숫자(MSD)나 최하위 유효숫자(LSD)에서 시작하도록 구현 가능
장점
- 비교 없이 정렬
- 문자열이나 정수 표현 정렬에 적합
단점
- 불안정 정렬
- 기수 테이블 크기의 메모리가 필요
- 부동소수점 실수처럼 특수한 비교 연산이 필요한 데이터에는 적용 불가
예시
기수가 자리수(1~3)이고, 기수 도메인이 0~9인 정수 정렬
1) 1의 자리수를 기준으로 버킷으로 분류
2) 버킷의 순서로 1차 정렬
3) 위 과정을 자리수만큼 반복
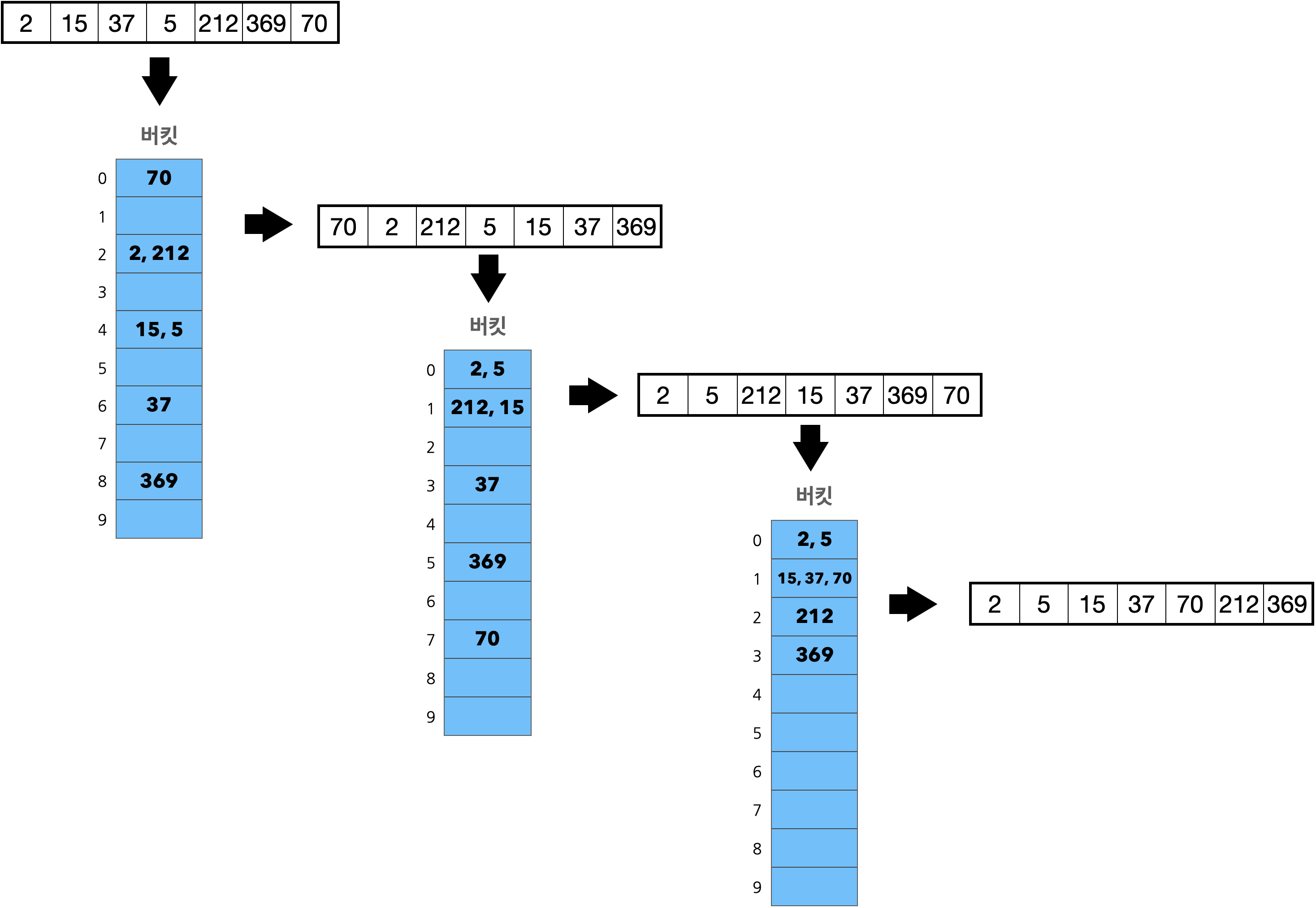
코드
func radixSort(_ array: [Int], maxDigit: Int) -> [Int] {
var arr = array
let radix = 10 // 기수의 도메인 크기
var bucket: [[Int]] = Array(repeating: [], count: radix) // 버킷
var digit = 1 // 자리수
for _ in 1...maxDigit { // 기수의 크기만큼 반복
for i in 0..<array.count {
bucket[(arr[i] / digit) % 10].append(arr[i])
}
arr = bucket.flatMap { $0 } // 버킷에 들어간 순서로 정렬
bucket = Array(repeating: [], count: radix) // 버킷 초기화
digit *= 10 // 자리수 증가
}
return arr
}
