17825: 주사위 윷놀이

풀이 시간

• 57m
• 백트래킹 문제 감을 잃어서 전체적인 아이디어 틀만 (살짝) 참고했다

구현 방식

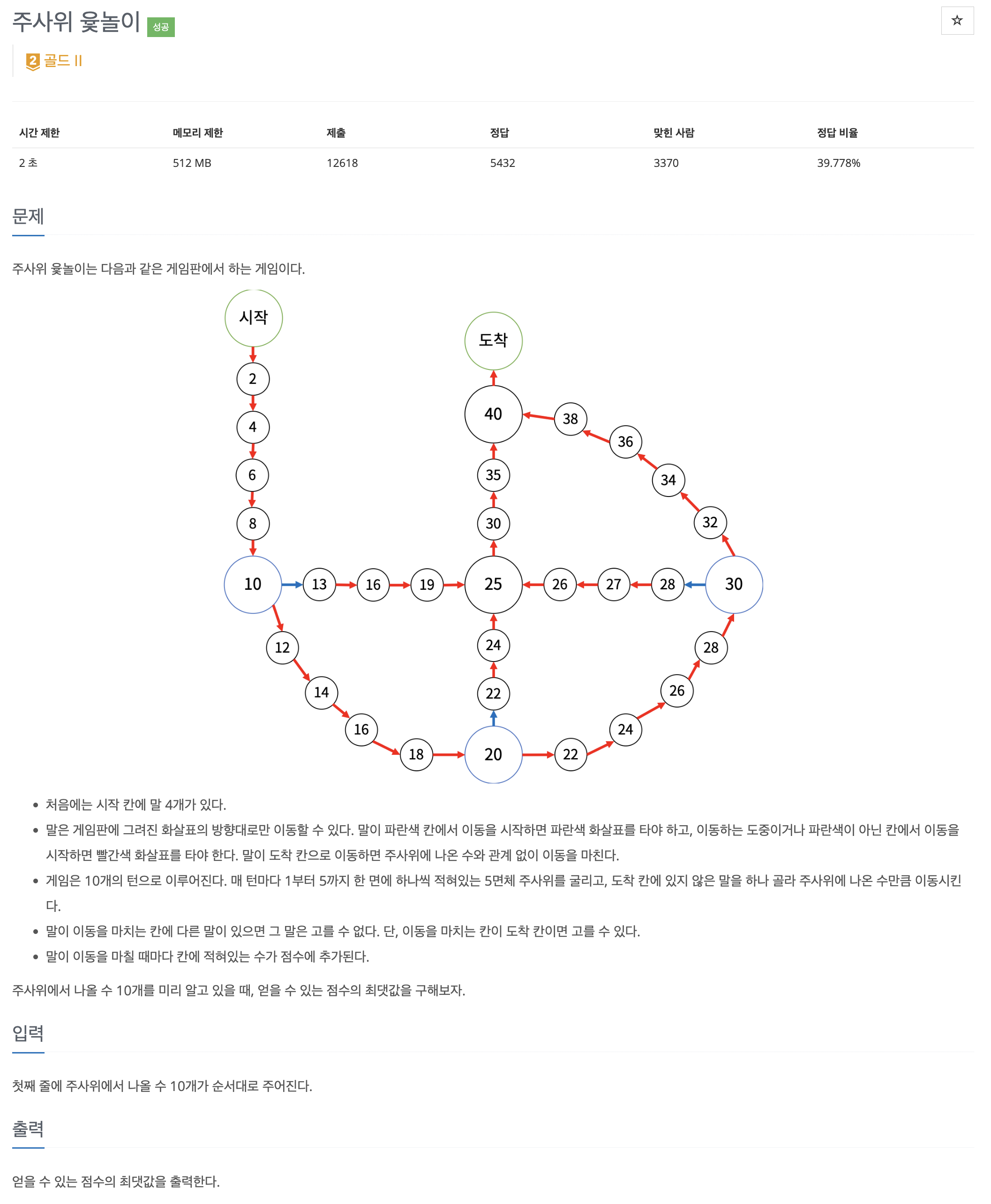
• 이 문제에서는 윷놀이판의 graph를 직접 작성해야한다
  -> graph: 인접 리스트 형태로, curr node당 next node를 매핑해줌. 파란색칸에 해당하는 node일 경우 1번 인덱스에 파란색 갈림길도 추가로 넣어줌. (처음 시작 위치가 파란칸이라면 바로 다음 위치를 graph[curr][1]로, 그렇지 않다면 graph[curr][0]으로 할당해줘야함)

• board_score는 node 위치 당 점수가 저장된 리스트이다 (이 부분도 직접 작성해줘야했다)

• backtracking 구현
  -> 종료조건: idx(dfs의 depth라고 보면 됨)가 dice의 길이(이 문제에선 10으로 고정임)와 같다면 max_score를 최댓값으로 갱신해주고 return
  
  
  -> horse의 길이(이 문제에선 4로 고정임)만큼 for문을 돌면서 일단 말을 dice[idx]만큼 이동시켜줌 (이 과정에서 처음 시작 위치(curr)가 파란칸이라면 바로 다음 위치를 graph[curr][1]로, 그렇지 않다면 graph[curr][0]으로 할당해주고, dice[idx]-1만큼 for문을 돌며 나머지 이동을 수행해줘야함)
  
  
  -> 이동이 끝난 말의 위치는 next이고, 문제의 조건 "말이 이동을 마치는 칸에 다른 말이 있으면 그 말은 고를 수 없다. 단, 이동을 마치는 칸이 도착 칸이면 고를 수 있다."에 따라 가능한 경우에만 재귀를 수행해줘야한다

코드

import sys

#위치 당 점수
board_score = [0, 2, 4, 6, 8, 10, 12, 14, 16, 18,
            20, 22, 24, 26, 28, 30, 32, 34, 36, 38,
            40, 13, 16, 19, 25, 22, 24, 28, 27, 26,
            30, 35, 0]
graph = [[1], [2], [3], [4], [5], [6, 21], [7], [8], [9], [10], [11, 25], [12], [13], [14], [15], [16, 27], [17], [18], [19], [20], [32], [22], [23], [24], [30], [26], [24], [28], [29], [24], [31], [20], [32]]

def backtracking(idx, score, horse):
    global max_score

    if idx == len(dice):
        max_score = max(max_score, score)
        return
    
    for i in range(len(horse)):
        curr = horse[i]

        ##### 주사위 수만큼 말 이동
        if len(graph[curr]) == 2:
            next = graph[curr][1]
        else:
            next = graph[curr][0]
        for j in range(dice[idx] - 1):
            next = graph[next][0]

        ##### 가능한 경우인지 확인하고, 가능하다면 진행
        if next == 32 or next not in horse:
            horse[i] = next
            backtracking(idx+1, score + board_score[next], horse)
            horse[i] = curr #for backtracking


dice = list(map(int, sys.stdin.readline()[:-1].split())) #주사위의 수

max_score = 0
backtracking(0, 0, [0, 0, 0, 0])
print(max_score)

결과