W7

Why us GNN?

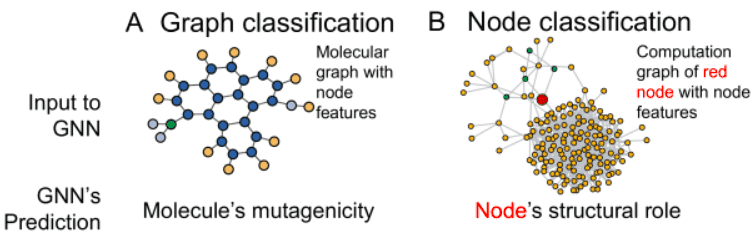
• 많은 data는 graph data structure로 표현될 수 있음
• GNN은 graph data를 input으로 받고, 다양한 downstream task (graph classification, node classification, link prediction)를 수행할 수 있음
• Node classification을 할거임

def encode_onehot(labels):
    classes = set(labels)
    classes_dict = {c: np.identity(len(classes))[i, :] for i, c in
                    enumerate(classes)}
    labels_onehot = np.array(list(map(classes_dict.get, labels)),
                             dtype=np.int32)
    return labels_onehot

• label information을 one-hot fixed size vector로 변환

def sparse_mx_to_torch_sparse_tensor(sparse_mx):
    """Convert a scipy sparse matrix to a torch sparse tensor."""
    sparse_mx = sparse_mx.tocoo().astype(np.float32)
    indices = torch.from_numpy(
        np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))
    values = torch.from_numpy(sparse_mx.data)
    shape = torch.Size(sparse_mx.shape)
    return torch.sparse.FloatTensor(indices, values, shape)

• adjacency matrix의 대부분은 0임 -> 그래서 sparse tensor of sparse matrix on scipy를 사용할거임
• 이 함수는 scipy sparse matrix를 torch sparse matrix로 바꿔줌

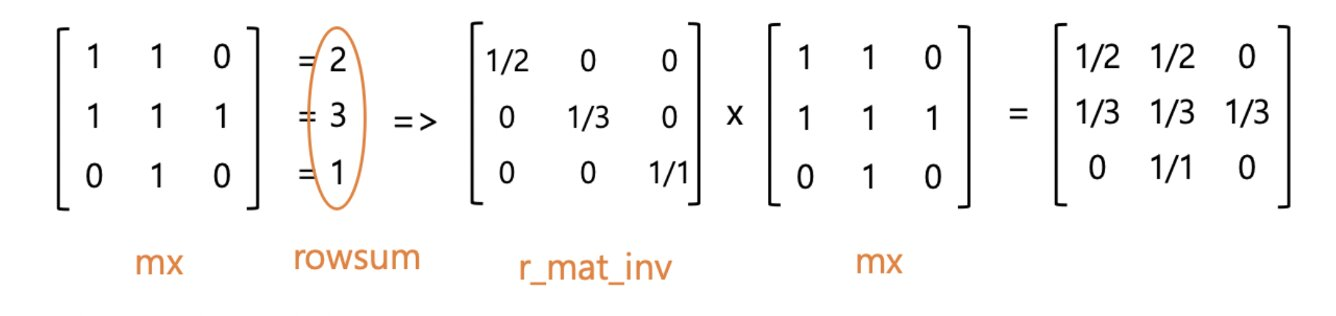
def normalize(mx):
    """Row-normalize sparse matrix"""
    rowsum = np.array(mx.sum(1))
    r_inv = np.power(rowsum, -1).flatten()
    r_inv[np.isinf(r_inv)] = 0.
    r_mat_inv = sp.diags(r_inv)
    mx = r_mat_inv.dot(mx)
    return mx

• adjacency matrix를 normalize 해줘야함 -> vanishing/exploding gradients를 피하기 위해
  

Graph data preprocessing

• Cora dataset
  # of nodes: 2708
  # of features: 1433
  # of labels: 7

# node data processing
node_data = np.genfromtxt(f"{path}{dataset}.content", dtype=np.dtype(str))
print(f"The number of nodes : {len(node_data)}")
print(node_data)

idx = np.array(node_data[:,0], dtype=np.int32)
features = sp.csr_matrix(node_data[:,1:-1], dtype=np.float32)
labels = encode_onehot(node_data[:,-1])

idx_map = {j: i for i, j in enumerate(idx)}

print(f'idx : {node_data[12,0]}')
print(f'a feature size : {len(node_data[12,1:-1])}, {node_data[12,1:-1]}')
print(f'a original label : {node_data[12,-1]}')
print(f"encoding label : {labels[12]}")

• node data processing

# edge data processing
edge_data = np.genfromtxt(f'{path}{dataset}.cites', dtype=np.int32)
edges = np.array(list(map(idx_map.get, edge_data.flatten())), dtype=np.int32)
edges = edges.reshape(edge_data.shape)

print(f'{len(edge_data)} \n raw data \n {edge_data[:10,]}')
print(f'\n start node -> end node \n {edges}')

• edge data processing

Graph Neural Network - Aggregation

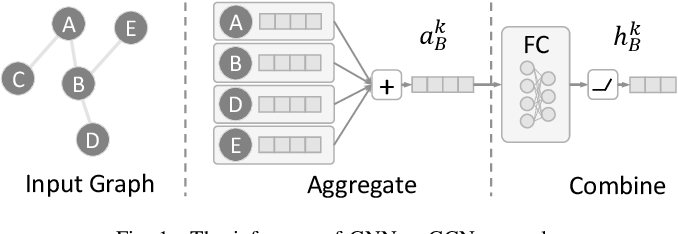
• GNN은 aggregation step, combine step으로 나뉨
• GNN은 neighbors로부터 정보를 aggregates함
• Adjacency matrix는 neighborhood information을 갖고있음
  

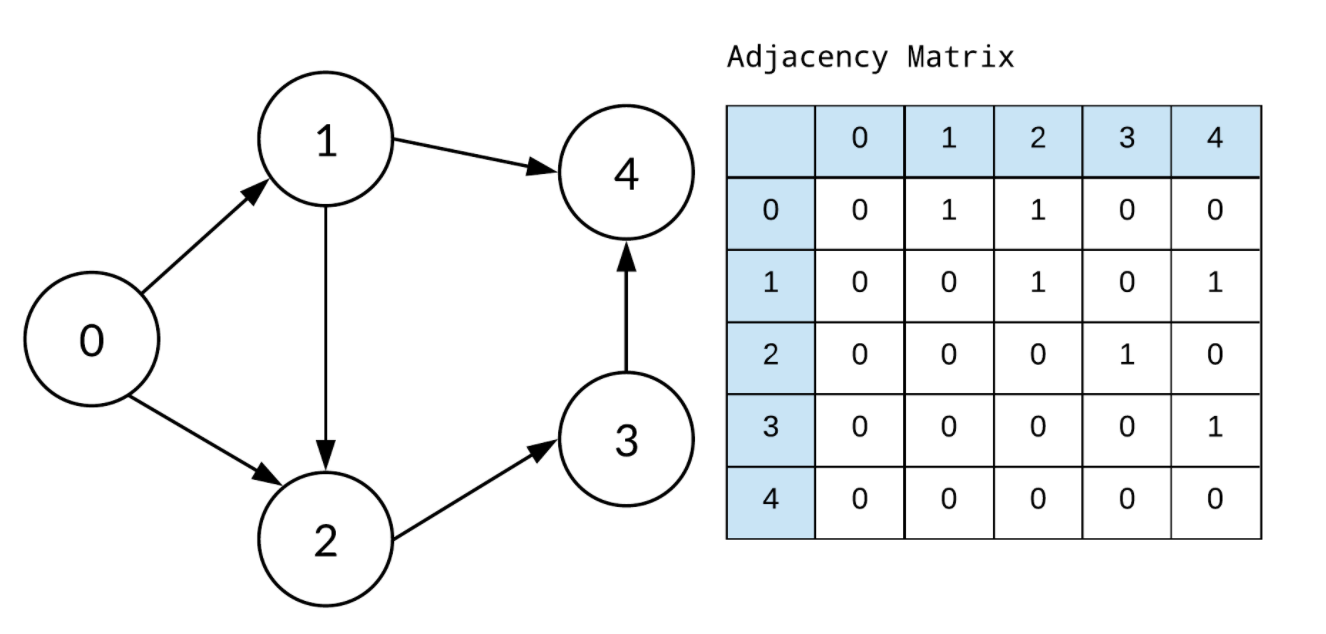
Symmetric adjacncy matrix

• 위의 예시는 directed graph임
• GNN model에서, 대부분의 edges는 undirected (bi-directd) edges임

Normalize the adjacency matrix

• information overload를 극복하기 위해, normalization이 필요함

adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:,0], edges[:,1])),
                    shape = (labels.shape[0], labels.shape[0]),
                    dtype = np.float32)
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)

# normalize
features = normalize(features)
adj = normalize(adj + sp.eye(adj.shape[0]))

Semi-supervised learning

# data split - semi supervised learning 
idx_train = range(140)
idx_val = range(200, 500)
idx_test = range(500, 1500) 

# tensorize
features = torch.FloatTensor(np.array(features.todense()))
labels = torch.LongTensor(np.where(labels)[1])
adj = sparse_mx_to_torch_sparse_tensor(adj)

idx_train = torch.LongTensor(idx_train)
idx_val = torch.LongTensor(idx_val)
idx_test = torch.LongTensor(idx_test)

Graph Neural Network - Combine

• neighbor로부터 정보를 받고나서, 이들을 combine 해줘야함
• 아래는 GNN model의 예시인 GCN의 equation임. message를 combine하기 위해 mean technique을 사용함 (normalized adjacency matrix를 사용하기 때문)
  

# GCN layer
class GraphConvolution(Module):
    def __init__(self, in_features, out_features, bias=True):
        super(GraphConvolution, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = Parameter(torch.FloatTensor(in_features, out_features))
        if bias:
            self.bias = Parameter(torch.FloatTensor(out_features))
        else:
            self.register_parameter('bias', None)
        self.reset_parameters()

    def reset_parameters(self):
        stdv = 1. / math.sqrt(self.weight.size(1))
        self.weight.data.uniform_(-stdv, stdv)
        if self.bias is not None:
            self.bias.data.uniform_(-stdv, stdv)

    def forward(self, input, adj):
        support = torch.mm(input, self.weight)
        output = torch.spmm(adj, support)
        if self.bias is not None:
            return output + self.bias
        else:
            return output

• 위의 equation에서 볼 수 있듯이, A * X * W는 recursive임. -> A * X * W를 수행하기 위한 class를 구현해야함

# model
class GCN(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout):
        super(GCN, self).__init__()

        self.gc1 = GraphConvolution(nfeat, nhid)
        self.gc2 = GraphConvolution(nhid, nclass)
        self.dropout = dropout

    def forward(self, x, adj):
        x = F.relu(self.gc1(x, adj))
        x = F.dropout(x, self.dropout, training=self.training)
        x = self.gc2(x, adj)
        return F.log_softmax(x, dim=1)

• equation에 두개의 recursive function이 있기 때문에, 여기서 두개의 GraphConvolution models을 정의함
• multiple GraphConvolution을 정의하는 것은 message가 얼마나 멀리 도달할 수 있는지를 결정함

#Main
import easydict

args = easydict.EasyDict({"no-cuda":False, "fastmode":False, "seed":42, \
                          "epochs":200, "lr":0.01, "weight_decay":5e-4, \
                          "hidden":16, "dropout":0.5, "cuda":True})

np.random.seed(args.seed)
torch.manual_seed(args.seed)

model = GCN(nfeat=1433, # num of features
            nhid=16,
            nclass=labels.max().item() + 1,
            dropout=args.dropout)

optimizer = optim.Adam(model.parameters(),
                       lr=args.lr, weight_decay=args.weight_decay)

if args.cuda:
    torch.cuda.manual_seed(args.seed)
    model.cuda()
    features = features.cuda()
    adj = adj.cuda()
    labels = labels.cuda()
    idx_train = idx_train.cuda()
    idx_val = idx_val.cuda()
    idx_test = idx_test.cuda()

• model 호출

def train(epoch):
    t = time.time()

    model.train()
    optimizer.zero_grad()
    #forward
    output = model(features, adj)

    #calculate loss 
    loss_train = F.nll_loss(output[idx_train], labels[idx_train]) #output of model, target
    acc_train = accuracy(output[idx_train], labels[idx_train]) #same with above

    loss_train.backward()
    optimizer.step()
    #calculate validation loss
    loss_val = F.nll_loss(output[idx_val], labels[idx_val])
    acc_val = accuracy(output[idx_val], labels[idx_val])
    print(f'[Epoch {epoch+1:04d}] Train_loss: {loss_train.item():.4f}, Train_accuracy: {acc_train.item():.4f},',
          f'Val_loss: {loss_val.item():.4f}, Val_accuracy: {acc_val.item():.4f}, \n #Time: {time.time() - t:.4f}')
    
def accuracy(output, labels):
    preds = output.max(1)[1].type_as(labels)
    correct = preds.eq(labels).double()
    correct = correct.sum()
    return correct / len(labels)
    
# train model
t_total = time.time()
for epoch in range(10):#args.epochs):
    train(epoch)
print(f"Total time elapsed: {time.time() - t_total:.4f}")

• train function 정의 및 training 진행

def test():
    model.eval()
    output = model(features, adj)

    loss_test = F.nll_loss(output[idx_test], labels[idx_test])
    acc_test = accuracy(output[idx_test], labels[idx_test])
    print("Test set results:",
          f"loss= {loss_test.item():.4f}",
          f"accuracy= {acc_test.item():.4f}")
          
# Testing
test()

• test function 정의 및 test 진행